| Россия, Новосибирск |
Выразимость в арифметике
Теорема 29. Всякая формула в 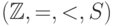 (где
(где 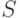 —
функция прибавления единицы) эквивалентна некоторой
бескванторной формуле. (Как говорят,
—
функция прибавления единицы) эквивалентна некоторой
бескванторной формуле. (Как говорят, 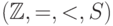 допускает элиминацию кванторов.)
допускает элиминацию кванторов.)
Полностью утверждение теоремы звучит так: для всякой формулы
сигнатуры, содержащей равенство, порядок и символ 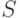 , найдется
бескванторная формула той же сигнатуры, которая эквивалентна ей
в интерпретации, где носителем является
, найдется
бескванторная формула той же сигнатуры, которая эквивалентна ей
в интерпретации, где носителем является 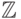 , а символы
сигнатуры интерпретируются естественным образом. (В дальнейшем
мы будем опускать такие пояснения.)
, а символы
сигнатуры интерпретируются естественным образом. (В дальнейшем
мы будем опускать такие пояснения.)
Доказательство следует прежней схеме. Правда, теперь атомарных
формул больше — помимо формул 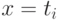 у нас будут формулы
у нас будут формулы  . Поэтому нельзя рассчитывать на то, что все значения
. Поэтому нельзя рассчитывать на то, что все значения  , не встречающиеся среди
, не встречающиеся среди 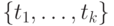 , ведут
себя одинаково, и наш прием с выделением случая, когда все равенства
ложны, более не проходит.
, ведут
себя одинаково, и наш прием с выделением случая, когда все равенства
ложны, более не проходит.
Как же быть? Для данных значений 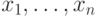 числа
числа  делят числовую ось (точнее, множество
делят числовую ось (точнее, множество 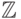 целых чисел) на промежутки, и для выяснения истинности формулы
целых чисел) на промежутки, и для выяснения истинности формулы 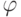 нам надо попробовать (помимо всех
нам надо попробовать (помимо всех 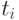 ) хотя
бы по одному числу из каждого промежутка. Это будет гарантировано,
если мы напишем дизъюнкцию, в которую, помимо всех формул
) хотя
бы по одному числу из каждого промежутка. Это будет гарантировано,
если мы напишем дизъюнкцию, в которую, помимо всех формул 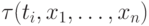 , войдут также формулы
, войдут также формулы 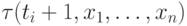 и
и 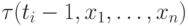 . Это
позволяет нам обойтись без формулы
. Это
позволяет нам обойтись без формулы 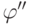 и благополучно
завершить доказательство.
и благополучно
завершить доказательство.
63. Проверьте, что добавление константы  к этой сигнатуре
не препятствует элиминации кванторов.
к этой сигнатуре
не препятствует элиминации кванторов.
Что будет, если мы из этой сигнатуры удалим функцию 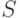 ? Легко
понять, что класс выразимых множеств не изменится, так как
? Легко
понять, что класс выразимых множеств не изменится, так как 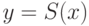 можно выразить как "
можно выразить как "  является наименьшим
элементом, большим
является наименьшим
элементом, большим  ". Однако при этом мы использовали
кванторы, так что для
". Однако при этом мы использовали
кванторы, так что для  элиминация
кванторов невозможна.
элиминация
кванторов невозможна.
64. Убедитесь, что в самом деле формула 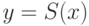 не
эквивалентна никакой бескванторной формуле этой сигнатуры.
не
эквивалентна никакой бескванторной формуле этой сигнатуры.
Часто такой переход приходится выполнять в обратном направлении: у нас есть некоторая ситуация, в которой элиминация кванторов не проходит. Мы обходим эту трудность, добавив некоторые выразимые предикаты и функции в нашу сигнатуру, после чего элиминация кванторов удается. В этом случае мы получаем описание всех выразимых предикатов (предикат выразим, если он записывается бескванторной формулой расширенной сигнатуры). Мы встретимся с такой ситуацией дальше, говоря об арифметике Пресбургера.
В некоторых случаях рассуждение упрощается, если использовать приведение бескванторной формулы к дизъюнктивной нормальной форме. Вот один из таких примеров.
Теорема 30. Всякая формула в  эквивалентна
некоторой бескванторной формуле.
эквивалентна
некоторой бескванторной формуле.
Как всегда, достаточно рассмотреть случай формулы вида
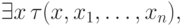
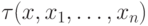 — бескванторная формула.
Формулу
— бескванторная формула.
Формулу 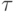 можно считать формулой в дизъюнктивной нормальной форме
(теорема 4). Напомним, это означает, что
можно считать формулой в дизъюнктивной нормальной форме
(теорема 4). Напомним, это означает, что 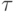 представляет
собой дизъюнкцию конъюнкций, а каждая конъюнкция соединяет
несколько литералов (атомарных формул или их отрицаний).
представляет
собой дизъюнкцию конъюнкций, а каждая конъюнкция соединяет
несколько литералов (атомарных формул или их отрицаний).В данном случае можно избавится от отрицаний, заменив 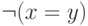 на
на 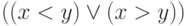 , а
, а 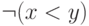 — на
— на 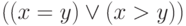 . После этого надо воспользоваться
дистрибутивностью и вновь придти к дизъюнктивной нормальной
форме — с большим числом членов, но уже без отрицаний.
. После этого надо воспользоваться
дистрибутивностью и вновь придти к дизъюнктивной нормальной
форме — с большим числом членов, но уже без отрицаний.
Теперь надо воспользоваться тем, что квантор
существования (который есть "бесконечная дизъюнкция") можно переставлять с дизъюнкцией.
Точнее говоря, мы пользуемся тем, что формулы 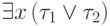 и
и 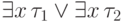 эквивалентны. (Белый или черный единорог существует тогда и
только тогда, когда существует белый единорог или существует
черный единорог.) Это обстоятельство позволяет заменить
формулу
эквивалентны. (Белый или черный единорог существует тогда и
только тогда, когда существует белый единорог или существует
черный единорог.) Это обстоятельство позволяет заменить
формулу
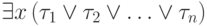
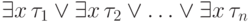
Итак, нам осталось преобразовать к бескванторному виду формулу
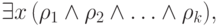
 соединяет какие-то две переменные
знаком
соединяет какие-то две переменные
знаком  или
или  (напомним, что от отрицаний мы уже
избавились).
(напомним, что от отрицаний мы уже
избавились).Некоторые из формул  не содержат переменной
не содержат переменной  . Тогда
их можно вынести за квантор: если
. Тогда
их можно вынести за квантор: если  не является параметром
формулы
не является параметром
формулы  , то формулы
, то формулы 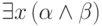 и
и 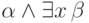 эквивалентны
(если
эквивалентны
(если  истинно для некоторых значений параметров, то
в обеих формулах его можно опустить; если
истинно для некоторых значений параметров, то
в обеих формулах его можно опустить; если  ложно, то
обе формулы ложны при этих значениях параметров).
ложно, то
обе формулы ложны при этих значениях параметров).
Вынеся такие формулы, можно считать, что под квантором остались
лишь формулы вида 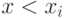 ,
, 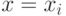 и
и 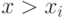 ,
сравнивающие переменную
,
сравнивающие переменную  с какими-то другими переменными. Если там
есть хоть одно равенство, то квантор существования вырождается —
его можно удалить вместе с переменной
с какими-то другими переменными. Если там
есть хоть одно равенство, то квантор существования вырождается —
его можно удалить вместе с переменной  , заменив ее на ту
переменную, которой она равна. Например, формулу
, заменив ее на ту
переменную, которой она равна. Например, формулу 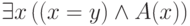 можно заменить на
можно заменить на 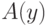 .
.
Итак, остался случай, когда переменная  встречается лишь в
неравенствах. Другими словами, нас спрашивают, найдется ли
значение
встречается лишь в
неравенствах. Другими словами, нас спрашивают, найдется ли
значение  , большее каких-то переменных и меньшее
каких-то других. Если все ограничения на
, большее каких-то переменных и меньшее
каких-то других. Если все ограничения на  одного знака
(только снизу или только сверху), то такое значение
одного знака
(только снизу или только сверху), то такое значение  существует при любых значениях других переменных (поскольку в множестве
существует при любых значениях других переменных (поскольку в множестве  нет
ни наибольшего, ни наименьшего элементов). Что делать, если
есть ограничения разных знаков? Пусть наша формула, например,
имеет вид
нет
ни наибольшего, ни наименьшего элементов). Что делать, если
есть ограничения разных знаков? Пусть наша формула, например,
имеет вид
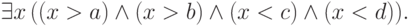
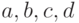 , при которых это верно,
не используя кванторов? Надо написать такую формулу:
, при которых это верно,
не используя кванторов? Надо написать такую формулу: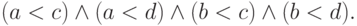
 является плотным (между любыми двумя элементами найдется
третий), то эта формула равносильна исходной.
является плотным (между любыми двумя элементами найдется
третий), то эта формула равносильна исходной.Так, постепенно сводя дело ко все более простым случаям, мы завершили рассуждение.
Заметим, что в этом доказательстве из свойств рациональных чисел
мы использовали лишь отсутствие наибольшего и наименьшего
элемента и плотность. Поэтому все наши преобразования остаются
эквивалентными для любого упорядоченного множества с такими
свойствами, а не только для  . Применив эти преобразования
к замкнутой формуле (формуле без параметров), мы получим или
тождественно истинную формулу, или тождественно ложную (только
надо добавить в язык константы для истины и лжи, чтобы не
использовать фиктивных переменных, когда надо написать
тождественно истинное или тождественно ложное выражение). Отсюда
мы заключаем, что во всех плотных упорядоченных множествах без
первого и последнего элемента справедливы одни и те же формулы
нашей сигнатуры. Как говорят, все такие множества элементарно эквивалентны с точки
зрения нашей сигнатуры. (Другое доказательство этого
факта можно получить, используя теорему Левенгейма-Сколема
о счетной подмодели и теорему об изоморфизме счетных
плотных линейно упорядоченных множеств без первого и
последнего элементов.)
. Применив эти преобразования
к замкнутой формуле (формуле без параметров), мы получим или
тождественно истинную формулу, или тождественно ложную (только
надо добавить в язык константы для истины и лжи, чтобы не
использовать фиктивных переменных, когда надо написать
тождественно истинное или тождественно ложное выражение). Отсюда
мы заключаем, что во всех плотных упорядоченных множествах без
первого и последнего элемента справедливы одни и те же формулы
нашей сигнатуры. Как говорят, все такие множества элементарно эквивалентны с точки
зрения нашей сигнатуры. (Другое доказательство этого
факта можно получить, используя теорему Левенгейма-Сколема
о счетной подмодели и теорему об изоморфизме счетных
плотных линейно упорядоченных множеств без первого и
последнего элементов.)
В частности, мы доказали, что для рациональных и
действительных чисел истинны одни и те же формулы сигнатуры  .
.
Еще одним побочным продуктом нашего рассуждения (как и других рассуждений об элиминации кванторов) является способ выяснить, будет ли данная замкнутая формула истинной или ложной в рассматриваемой интерпретации. Для этого надо привести ее к бескванторному виду и посмотреть, получится ли И или Л. Другими словами, элиминация кванторов устанавливает разрешимость элементарной теории рациональных чисел с отношениями равенства и порядка.
Элиминация кванторов остается возможной (и рассуждение даже
немного упрощается), если рациональные (или действительные)
числа рассматривать не только с равенством и порядком, но и со
сложением и рациональными константами.
В этом случае можно воспользоваться приведенной ранее схемой с конечным
представительным набором термов. В самом деле, пусть  —
переменная, которую (вместе с квантором существования по ней) мы
хотим элиминировать. Все атомарные формулы, ее содержащие, можно
"разрешить" относительно
—
переменная, которую (вместе с квантором существования по ней) мы
хотим элиминировать. Все атомарные формулы, ее содержащие, можно
"разрешить" относительно  , получив некоторое количество
формул вида
, получив некоторое количество
формул вида 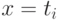 ,
,  и
и  , где
, где 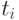 — линейные комбинации
остальных переменных с рациональными коэффициентами. (Разрешение
рациональных коэффициентов вместо целых ничего не меняет, так как можно
привести все к общему знаменателю и получить целые коэффициенты,
затем перенести отрицательные коэффициенты в другую часть, а
положительные заменить многократным сложением.)
— линейные комбинации
остальных переменных с рациональными коэффициентами. (Разрешение
рациональных коэффициентов вместо целых ничего не меняет, так как можно
привести все к общему знаменателю и получить целые коэффициенты,
затем перенести отрицательные коэффициенты в другую часть, а
положительные заменить многократным сложением.)
Затем в качестве представительного набора надо взять набор,
состоящий, во-первых, из всех 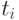 , во-вторых, из всех средних
арифметических
, во-вторых, из всех средних
арифметических 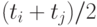 , и, наконец, из выражений
, и, наконец, из выражений  и
и 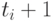 . Ясно, что как бы ни расположились точки
. Ясно, что как бы ни расположились точки 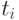 на
числовой оси, этот набор захватит как минимум по одной точке из
каждого промежутка (средние арифметические нужны для интервалов,
а прибавление и вычитание единицы — для лучей по краям).
на
числовой оси, этот набор захватит как минимум по одной точке из
каждого промежутка (средние арифметические нужны для интервалов,
а прибавление и вычитание единицы — для лучей по краям).
65. Провести это рассуждение подробно.
Возможность элиминации кванторов в только что рассмотренной ситуации ( 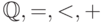 , рациональные константы) имеет
интересное геометрическое применение.
, рациональные константы) имеет
интересное геометрическое применение.
