| Россия, Новосибирск |
Языки первого порядка
Помимо логических связок, в математических рассуждениях часто
встречаются кванторы "для любого" ( 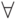 ) и "существует" (
) и "существует" (  ).
Например, определение непрерывности начинается словами "для
любого положительного
).
Например, определение непрерывности начинается словами "для
любого положительного  найдется положительное
найдется положительное  , для которого, ...". А одна из аксиом
теории групп (существование обратного элемента) записывается так:
, для которого, ...". А одна из аксиом
теории групп (существование обратного элемента) записывается так: 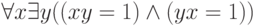 .
.
Можно сформулировать различные логические законы, включающие в
себя кванторы. Например, высказывание "существует такое  ,
что
,
что  " (где
" (где  — некоторое свойство объекта
— некоторое свойство объекта  ) логически эквивалентно высказыванию "не для всех
) логически эквивалентно высказыванию "не для всех  верно
верно 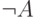 ".
".
Мы будем записывать такого рода законы с помощью формул, дадим определение истинности формул (при данной интерпретации входящих в них символов) и исследуем, какого рода свойства можно выражать с помощью формул и какие нельзя.
Формулы и интерпретации
Начнем с примера. Пусть  — некоторое непустое множество, а
— некоторое непустое множество, а  — бинарное отношение на нем, то есть подмножество
декартова произведения
— бинарное отношение на нем, то есть подмножество
декартова произведения  . Вместо
. Вместо 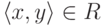 мы будем писать
мы будем писать 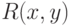 .
Рассмотрим формулу
.
Рассмотрим формулу
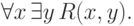
 (для любого элемента
(для любого элемента 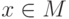 найдется элемент, находящийся с
ним в отношении
найдется элемент, находящийся с
ним в отношении  ) и может быть истинна или ложна. Например,
если
) и может быть истинна или ложна. Например,
если  есть множество натуральных чисел
есть множество натуральных чисел  , а
, а  — отношение "строго меньше" (другими словами,
— отношение "строго меньше" (другими словами,  есть
множество всех пар
есть
множество всех пар 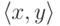 , для которых
, для которых  ), то эта формула истинна. А для отношения "строго больше"
(на том же множестве) эта формула ложна.
), то эта формула истинна. А для отношения "строго больше"
(на том же множестве) эта формула ложна.Вопрос о том, будет ли истинна формула

 и для данного бинарного отношения
и для данного бинарного отношения  на нем, не имеет смысла, пока не уточнено, каково значение
переменной
на нем, не имеет смысла, пока не уточнено, каково значение
переменной  . Например, если
. Например, если 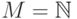 и
и 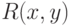 есть
есть  , то эта формула будет истинной при
, то эта формула будет истинной при 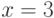 и
ложной при
и
ложной при 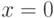 . Для данных
. Для данных  и
и  она задает
некоторое свойство элемента
она задает
некоторое свойство элемента  и тем самым определяет некоторое подмножество
множества
и тем самым определяет некоторое подмножество
множества  .
.Перейдем к формальным определениям. Пусть  — непустое
множество. Множество
— непустое
множество. Множество  состоит из всех последовательностей
состоит из всех последовательностей  длины
длины  , составленных из
элементов множества
, составленных из
элементов множества  . Назовем
. Назовем  -местной
функцией на множестве
-местной
функцией на множестве  любое отображение
любое отображение  в
в  (определенное на всем
(определенное на всем  ). Синонимы: "функция
). Синонимы: "функция  аргументов",
"функция валентности
аргументов",
"функция валентности  ", "функция местности
", "функция местности  " и даже "функция арности
" и даже "функция арности  " (последнее слово происходит от слов
"унарная" для функций одного аргумента, "бинарная"
(операция) для функций двух аргументов и "тернарная" для трех аргументов).
" (последнее слово происходит от слов
"унарная" для функций одного аргумента, "бинарная"
(операция) для функций двух аргументов и "тернарная" для трех аргументов).
Назовем  -местным предикатом на множестве
-местным предикатом на множестве  любое
отображение
любое
отображение  в множество
в множество  . Такой
предикат будет истинным на некоторых наборах
. Такой
предикат будет истинным на некоторых наборах  множества
множества  и ложным на остальных
наборах. Поставив ему в соответствие множество тех наборов, где
он истинен, мы получаем взаимно однозначное соответствие между
и ложным на остальных
наборах. Поставив ему в соответствие множество тех наборов, где
он истинен, мы получаем взаимно однозначное соответствие между  -местными предикатами на
-местными предикатами на  и подмножествами
множества
и подмножествами
множества  . Говоря о предикатах, также употребляют термины
"валентность", "число аргументов" и др.
. Говоря о предикатах, также употребляют термины
"валентность", "число аргументов" и др.
Мы будем рассматривать также функции и предикаты валентности нуль.
Множество  одноэлементно (содержит единственную
последовательность длины
одноэлементно (содержит единственную
последовательность длины  ). Поэтому функции
). Поэтому функции 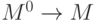 отождествляются с элементами множества
отождествляются с элементами множества  , а нульместных
предикатов ровно два — истинный и ложный.
, а нульместных
предикатов ровно два — истинный и ложный.
Естественно, что в формулы будут входить не сами функции и предикаты, а обозначения для них, которые называют функциональными и предикатными символами. В качестве символов можно использовать любые знаки. Важно лишь, что каждому символу приписана валентность, которая определяет, со сколькими аргументами он может встречаться в формуле. Произвольный набор предикатных и функциональных символов, для каждого из которых указано неотрицательное число, называемое валентностью, мы будем называть сигнатурой.
Остается определить три вещи: что такое формула данной сигнатуры, что такое интерпретация данной сигнатуры и когда формула является истинной (в данной интерпретации).
Фиксируем некоторый набор символов, называемых индивидными
переменными. Они предназначены для обозначения элементов
множества, на котором определены функции и предикаты; обычно
в таком качестве используют латинские буквы  с индексами. В каждой формуле будет использоваться
конечное число переменных, так что счетного набора переменных
нам хватит. Мы предполагаем, что переменные отличны от всех
функциональных и предикатных символов сигнатуры (иначе выйдет
путаница).
с индексами. В каждой формуле будет использоваться
конечное число переменных, так что счетного набора переменных
нам хватит. Мы предполагаем, что переменные отличны от всех
функциональных и предикатных символов сигнатуры (иначе выйдет
путаница).
