| Россия, Новосибирск |
Языки первого порядка
Определим понятие терма данной сигнатуры. Термом называется последовательность переменных, запятых, скобок и символов сигнатуры, которую можно построить по следующим правилам:
- Индивидная переменная есть терм.
- Функциональный символ валентности
 есть терм.
есть терм. - Если
 — термы, а
— термы, а  — функциональный
символ валентности
— функциональный
символ валентности  , то
, то 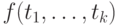 есть терм.
есть терм.
В принципе можно было не выделять функциональные символы
валентности  (которые также называют константами)
в отдельную группу, но тогда бы после них
пришлось писать скобки (как это делается в программах на языке Си).
(которые также называют константами)
в отдельную группу, но тогда бы после них
пришлось писать скобки (как это делается в программах на языке Си).
Если  — предикатный символ валентности
— предикатный символ валентности  , а
, а  — термы, то выражение
— термы, то выражение 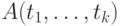 считается атомарной формулой. Кроме того, любой
предикатный символ валентности
считается атомарной формулой. Кроме того, любой
предикатный символ валентности  считается атомарной формулой.
считается атомарной формулой.
Формулы строятся по таким правилам:
- Атомарная формула есть формула.
- Если
 — формула, то
— формула, то 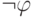 — формула.
— формула. - Если
 и
и  — формулы, то выражения
— формулы, то выражения 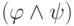 ,
, 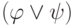 ,
,  также являются формулами.
также являются формулами. - Если
 есть формула, а
есть формула, а  — индивидная
переменная, то выражения
— индивидная
переменная, то выражения  и
и 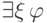 являются формулами.
являются формулами.
Во многих случаях в сигнатуру входит двуместный предикатный
символ  , называемый равенством.
По традиции вместо
, называемый равенством.
По традиции вместо 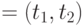 пишут
пишут  .
.
Итак, понятие формулы в данной сигнатуре полностью определено. Иногда такие формулы называют формулами первого порядка данной сигнатуры, или формулами языка первого порядка с данной сигнатурой.
Наш следующий шаг — определение интерпретации
данной сигнатуры. Пусть фиксирована некоторая сигнатура  . Чтобы
задать интерпретацию сигнатуры
. Чтобы
задать интерпретацию сигнатуры  , необходимо:
, необходимо:
- указать некоторое непустое множество
 ,
называемое носителем интерпретации;
,
называемое носителем интерпретации; - для каждого предикатного символа сигнатуры
 указать
предикат с соответствующим числом аргументов, определенный
на множестве
указать
предикат с соответствующим числом аргументов, определенный
на множестве  (как мы уже говорили,
(как мы уже говорили,  -местным предикатным символам ставится в соответствие
либо И, либо Л );
-местным предикатным символам ставится в соответствие
либо И, либо Л ); - для каждого функционального символа сигнатуры
 указать функцию соответствующего числа аргументов с аргументами
и значениями из
указать функцию соответствующего числа аргументов с аргументами
и значениями из  (в частности, для
(в частности, для  -местных
функциональных символов надо указать элемент множества
-местных
функциональных символов надо указать элемент множества  , с ними сопоставляемый).
, с ними сопоставляемый).
Если сигнатура включает в себя символ равенства, то среди ее
интерпретаций выделяют нормальные
интерпретации, в которых символ равенства интерпретируется как совпадение
элементов множества  .
.
Приведем несколько примеров сигнатур, используемых в различных теориях.
Сигнатура теории упорядоченных множеств включает
в себя два двуместных предикатных символа (равенство и
порядок) и не имеет функциональных символов. Здесь также
вместо  по традиции пишут
по традиции пишут  .
.
Аксиомы порядка (рефлексивность, антисимметричность, транзитивность) могут быть записаны формулами этой сигнатуры. Например, требование антисимметричности записывается так:
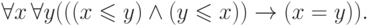
Иногда в сигнатуру теории упорядоченных множеств вместо символа  включают символ
включают символ 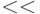 ; большой разницы тут нет.
; большой разницы тут нет.
39. Как записать с помощью формулы свойство линейной упорядоченности? свойство не иметь наибольшего элемента? свойство плотности (отсутствия соседних элементов)? свойство фундированности (отсутствия бесконечных убывающих последовательностей — или, что эквивалентно, наличия минимального элемента в любом подмножестве)? свойство полной упорядоченности? (Указание: не для всех перечисленных свойств это возможно.)
Сигнатуру теории групп можно выбирать по-разному. Можно
считать, что (помимо равенства) она имеет двуместный
функциональный символ 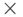 (который по традиции записывают
между множителями), константу (нульместный функциональный
символ)
(который по традиции записывают
между множителями), константу (нульместный функциональный
символ)  и одноместный функциональный символ
и одноместный функциональный символ  для обращения. Тогда аксиомы теории групп записываются с
использованием лишь кванторов всеобщности:
для обращения. Тогда аксиомы теории групп записываются с
использованием лишь кванторов всеобщности:
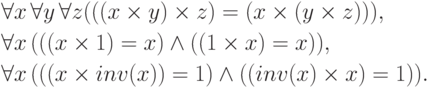
Если не включать операцию обращения в сигнатуру, придется использовать квантор существования и переписать последнюю аксиому так:
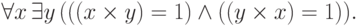
40. Как записать аксиомы теории групп, если в сигнатуре нет
константы  ?
(Указание: аксиома о существовании обратного станет частью аксиомы
о существовании единицы.)
?
(Указание: аксиома о существовании обратного станет частью аксиомы
о существовании единицы.)
41. Как записать в виде формулы требование коммутативности
группы? утверждение о том, что любой элемент (кроме единицы)
имеет порядок  ? конечность группы? (Указание: не все из
перечисленного можно записать, хотя пока у нас нет средств это
установить.)
? конечность группы? (Указание: не все из
перечисленного можно записать, хотя пока у нас нет средств это
установить.)
Сигнатура теории множеств содержит два двуместных предикатных символа: для принадлежности и для равенства. Аксиомы теории множеств можно записывать в виде формул этой сигнатуры. Чаще всего рассматривают вариант аксиоматической теории множеств, называемый теорией Цермело-Френкеля и обозначаемый ZF. Приведем для примера одну из аксиом теории ZF, называемую аксиомой объемности, или экстенсиональности:
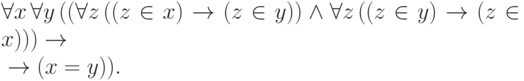
42. Сформулировать словесно эту аксиому.
43. Записать в виде формулы аксиому регулярности, или фундирования,
которая говорит, что у всякого множества есть минимальный (с точки зрения
отношения 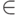 ) элемент, то есть элемент, не пересекающийся с самим
множеством.
) элемент, то есть элемент, не пересекающийся с самим
множеством.
44. Какова естественная сигнатура для теории полей? Можно ли
записать в виде формулы этой сигнатуры утверждение о том, что
поле имеет характеристику  ? конечную характеристику?
алгебраически замкнуто?
? конечную характеристику?
алгебраически замкнуто?
