| Россия |
Приложение. Параллельные вычисления на кластерах из персональных компьютеров в математической физике (В.Е.Карпов, А.И.Лобанов)
5. Выбор модели организации параллельных вычислений
Для решения уравнения (8) был выбран достаточно простой алгоритм, внутренний параллелизм которого практически очевиден. Тем не менее, для определения эффективной модели распараллеливания целесообразно использование системы
анализа программ на параллельность BERT 77 (http://www.plogic.com/bert-des.html). BERT 77 опирается на полученные оценки выполнения элементарных конструкций языка программирования FORTRAN 77 без предварительного исполнения анализируемой программы. Эти оценки строятся для каждой тройки: вычислительная система, компилятор, система коммуникации. Были проведены исследования для разных комбинаций компонентов тройки. Они показали, что времена выполнения программных конструкций (включая вычисление выражений, организацию циклов, доступ к элементам многомерных массивов, организацию вызовов функций и подпрограмм) могут быть оценены при использовании небольшого количества
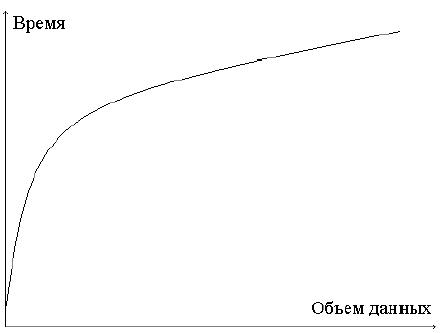
(порядка 200 ) предварительно вычисленных времен выполнения элементарных операций для конкретной пары "вычислительная система-компилятор". Эксперименты по измерению скоростей передачи информации для различных коммуникационных систем приводят к зависимости времени передачи данных от их объема, подобной изображенной на рис. 2. Такие зависимости в системе BERT 77 приближаются непрерывными кусочно-линейными функциями вида 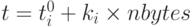 при
при  , где ni пробегает значения 0, 1024, 2048, 4096 и т.д., t — полное время передачи данных, - латентности, ki — скорости передачи, а nbytes — количество передаваемых данных.
, где ni пробегает значения 0, 1024, 2048, 4096 и т.д., t — полное время передачи данных, - латентности, ki — скорости передачи, а nbytes — количество передаваемых данных.
Проанализируем эффективность различных моделей организации вычислений.
5.1. Потоковая модель
Входными переменными для параллельного яруса являются значения потенциала  во всех узлах сетки на предыдущей итерации, а выходными —
значения потенциала на текущей итерации и значение относительной погрешности (5).
Относительная погрешность является редукционной переменной по отношению к операции min, т.е. ее частичные значения могут быть вычислены на рабочих процессорах, а окончательное значение — применением редукционной операции при приеме частичных значений. Если задействовано N рабочих процессоров, то при идеальной балансировке загрузки время выполнения вычислений будет составлять
во всех узлах сетки на предыдущей итерации, а выходными —
значения потенциала на текущей итерации и значение относительной погрешности (5).
Относительная погрешность является редукционной переменной по отношению к операции min, т.е. ее частичные значения могут быть вычислены на рабочих процессорах, а окончательное значение — применением редукционной операции при приеме частичных значений. Если задействовано N рабочих процессоров, то при идеальной балансировке загрузки время выполнения вычислений будет составлять 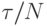 .
.
Количество узлов сетки на один процессор при нарезке рабочих областей по вертикали и правильной балансировке вряд ли будет различаться на двоичный порядок. Поэтому объемы передаваемых данных попадут на один участок кусочно-линейной
аппроксимации, скажем, на участок j. Скорость передачи информации на нем составляет kj байтов в единицу времени. Если главный процессор будет отправлять рабочему процессору с номером i nbytesi байт, то время передачи составит 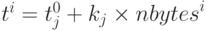 . Полное время передачи входных данных главным процессором при использовании 8-байтовых данных будет
. Полное время передачи входных данных главным процессором при использовании 8-байтовых данных будет 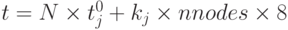 , где nnodes — полное число узлов расчетной сетки. Независимо от значений N и j это время на порядок превышает время выполнения одной итерации. Даже без анализа передачи выходной информации видна неэффективность модели на имеющейся конфигурации
вычислительной системы.
, где nnodes — полное число узлов расчетной сетки. Независимо от значений N и j это время на порядок превышает время выполнения одной итерации. Даже без анализа передачи выходной информации видна неэффективность модели на имеющейся конфигурации
вычислительной системы.
5.2. Динамическая модель
В динамической модели передача входных данных от главного процессора к рабочим отсутствует. Но вычисленные значения потенциала и относительной погрешности должны быть широковещательно разосланы всем процессорам. Аналогично получаем ту же оценку времени вычислений на одном процессоре — 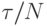 и оценку снизу для времени передачи данных
и оценку снизу для времени передачи данных 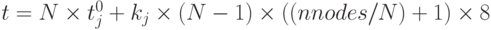 , которые доказывают неэффективность применения и этой модели.
, которые доказывают неэффективность применения и этой модели.