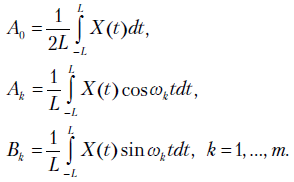|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Методологические вопросы прогнозирования временных рядов
5.6. Гармонический анализ временных рядов
Предположим, временной ряд  может быть представлен в виде суммы
может быть представлен в виде суммы
где
После удаления тренда  одним из описанных выше методов в остатках ряда
одним из описанных выше методов в остатках ряда  будет присутствовать периодическая составляющая
будет присутствовать периодическая составляющая  . Это приведет к обнаружению автокорреляции в остатках при проверке по критерию Неймана или Дарбина - Ватсона. Рассмотрим методы выделения периодической составляющей тренда временного ряда.
. Это приведет к обнаружению автокорреляции в остатках при проверке по критерию Неймана или Дарбина - Ватсона. Рассмотрим методы выделения периодической составляющей тренда временного ряда.
Задача гармонического анализа - определить основные гармонические колебания, входящие в периодическую составляющую ряда  и определяющие основные закономерности развития исследуемого процесса.
и определяющие основные закономерности развития исследуемого процесса.
Рассмотрим математическую постановку задачи гармонического анализа.
Пусть на конечном интервале ![[-L; L]](/sites/default/files/tex_cache/146bbde98490e13d8b4f4259e012b7df.png) задана функция
задана функция  , где
, где  - периодическая функция, а
- периодическая функция, а  - случайная составляющая, причем
- случайная составляющая, причем  . Функция
. Функция  считается полностью определенной, если известны период
считается полностью определенной, если известны период (или частоты
(или частоты 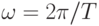 ) и коэффициенты ряда Фурье
) и коэффициенты ряда Фурье
Задача считается решенной, если определены параметры  .
.
Будем искать расчетную функцию  :
:
где
Определим эти параметры с помощью метода наименьших квадратов, минимизируя функцию
Доказано, что для выбранных заранее \omega _{k} решение задачи МНК может быть получено в виде
Следует отметить, что основными трудностями при гармоническом анализе временного ряда являются определение частот  и вычисление интегралов по формулам (5.22).
и вычисление интегралов по формулам (5.22).
Контрольные вопросы
- Каковы основные принципы прогнозирования экономических процессов?
- Что такое метод и модель прогнозирования?
- Что такое случайный процесс?
- Какие характеристики случайного процесса вы знаете?
- Какие условия характеризуют стационарный случайный процесс?
- Опишите процесс построения коррелограммы.
- Нарисуйте схематические графики коррелограмм для различных случайных процессов: нестационарного, белого шума, стационарного процесса, временного ряда с периодической компонентой.
- Какие подходы можно использовать для выделения тренда нестационарного временного ряда?
- Какие проблемы возникают при наличии автокорреляции остатков временного ряда?
- В чем заключается критерий поворотных точек для обнаружения положительной корреляции остатков ряда?
- Как используются критерии Неймана и Дарбина - Ватсона для обнаружения автокорреляции остатков?
- Опишите методику и приведите расчетные формулы для получения периодической компоненты ряда методом гармонического анализа.



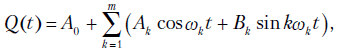

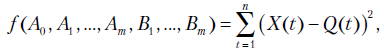

 .
.