| Россия |
Эксперименты с автоматами, имеющими взвешенный входной алфавит
Синтез установочных последовательностей, минимальных по весу
Для построения минимальной по весу УП используем граф, который назовем установочным деревом (УД). Основой для его построения является описанное выше дерево преемников. При обозначении вершин дерева на рисунках будем придерживаться следующего правила: состояния  -множества отделяются друг от друга запятой, а одно
-множества отделяются друг от друга запятой, а одно  -множество от другого в пределах
-множество от другого в пределах  -группы отделяется точкой с запятой.
-группы отделяется точкой с запятой.
УД строится точно так же, как СД, а правила, по которым вершина 
 -го уровня дерева преемников становится листом, таковы:
-го уровня дерева преемников становится листом, таковы:
- она является однородной;
- она является простой;
- на уровнях, предшествующих
 -му, имеется такая вершина
-му, имеется такая вершина 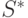 , что
, что 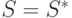 , но значение флажка вершины
, но значение флажка вершины  больше значения флажка вершины
больше значения флажка вершины 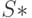 ;
; - на уровнях, предшествующих
 -му, имеется однородная или простая вершина
-му, имеется однородная или простая вершина 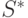 , значение флажка которой меньше значения флажка вершины
, значение флажка которой меньше значения флажка вершины  .
.
Заметим, что для превращения вершины  в лист достаточно выполнения одного из четырех перечисленных пунктов.
в лист достаточно выполнения одного из четырех перечисленных пунктов.
Прокомментируем эти правила. Пункт 3 правил означает, что в УД уже имеется более "легкий" по весу отрезок пути, приводящий к некоторой  -группе, чем путь, приведший к вершине
-группе, чем путь, приведший к вершине  с точно такой же
с точно такой же  -группой. Понятно, что при продолжении построения УД из вершины
-группой. Понятно, что при продолжении построения УД из вершины  принципиально возможно построить некоторую УП, но вес ее заведомо не может быть минимальным. Именно это является причиной того, что дальнейшее продолжение пути из
принципиально возможно построить некоторую УП, но вес ее заведомо не может быть минимальным. Именно это является причиной того, что дальнейшее продолжение пути из  в
в  не производится, т. е. этот путь обрывается.
не производится, т. е. этот путь обрывается.
Пункт 4 правил означает, что если в УД на некотором уровне меньше  -го уже имеется путь, приведший к синтезу УП определенного веса, то продолжение поиска УП на пути от
-го уже имеется путь, приведший к синтезу УП определенного веса, то продолжение поиска УП на пути от  к
к  и далее если и даст положительный результат, то заведомо приведет к синтезу новой УП большего веса, чем ранее найденная. Поскольку такая УП не представляет интереса, то путь из
и далее если и даст положительный результат, то заведомо приведет к синтезу новой УП большего веса, чем ранее найденная. Поскольку такая УП не представляет интереса, то путь из  в
в  продолжать не имеет смысла.
продолжать не имеет смысла.
Легко сообразить, что если некоторая вершина  дерева преемников становится листом вследствие выполнения пунктов 1 и/или 2 правил, то последовательность входных символов, соответствующая пути в УД из корня в вершину
дерева преемников становится листом вследствие выполнения пунктов 1 и/или 2 правил, то последовательность входных символов, соответствующая пути в УД из корня в вершину  , является УП. Отсюда вытекает следующая процедура построения УП с минимальным весом. Среди всех вершин УД, являющихся листьями, которым соответствуют однородные и/или простые
, является УП. Отсюда вытекает следующая процедура построения УП с минимальным весом. Среди всех вершин УД, являющихся листьями, которым соответствуют однородные и/или простые  -группы состояний рассматриваемого автомата, отыскивается вершина
-группы состояний рассматриваемого автомата, отыскивается вершина  с минимальным значением
с минимальным значением 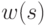 флажка. Входная последовательность, соответствующая пути из корня УД в вершину
флажка. Входная последовательность, соответствующая пути из корня УД в вершину  , и является УП с минимальным весом, равным
, и является УП с минимальным весом, равным 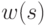 .
.
Проиллюстрируем процесс построения УП для автомата, заданного табл. 1.1, полагая, что  . УД для этого автомата изображено на рис.1.2. Вершины УД, являющиеся однородными или простыми, отмечены знаком "+". Всего таких вершин в УД имеется 16, из которых вершина
. УД для этого автомата изображено на рис.1.2. Вершины УД, являющиеся однородными или простыми, отмечены знаком "+". Всего таких вершин в УД имеется 16, из которых вершина  второго уровня имеет минимальное значение флажка, равное 15. Поскольку пути в УД из корня в эту вершину соответствует входная последовательность
второго уровня имеет минимальное значение флажка, равное 15. Поскольку пути в УД из корня в эту вершину соответствует входная последовательность 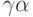 , то она и является минимальной по весу УП. Заметим, что в данном примере эта УП является одновременно и минимальной по длине, однако в общем случае этот факт места не имеет.
, то она и является минимальной по весу УП. Заметим, что в данном примере эта УП является одновременно и минимальной по длине, однако в общем случае этот факт места не имеет.
Синтез диагностических последовательностей, минимальных по весу
Для построения минимальной по весу ДП используем граф, который назовем диагностическим дерево (ДД). Его построение осуществляется точно так же, как и построение УД, но при этом используются несколько иные правила обрыва ветвей дерева приемников.
При построении ДД автомата  с множеством
с множеством  допустимых начальных состояний вершина
допустимых начальных состояний вершина 
 -го уровня становится листом, если выполняется хотя бы одно из следующих условий:
-го уровня становится листом, если выполняется хотя бы одно из следующих условий:
- она является простой;
- она является кратной;
- на уровнях, предшествующих
 -му, имеется такая вершина
-му, имеется такая вершина 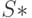 , что
, что 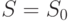 , но значение флажка вершины
, но значение флажка вершины  больше значения флажка вершины
больше значения флажка вершины 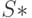 ;
; - на уровнях, предшествующих
 -му, имеется простая вершина
-му, имеется простая вершина 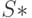 , значение флажка которой меньше значения флажка вершины
, значение флажка которой меньше значения флажка вершины  .
.
Прокомментируем эти правила. Выполнение пункта 1 этих правил означает, что рассматриваемый автомат имеет ДП, которая соответствует входной последовательности на пути в ДД, ведущем из его корня в простую вершину  . Выполнение пункта 2 правил означает, что существует такая последовательность, подача которой на вход автомата, находящегося в различных состояниях из множества
. Выполнение пункта 2 правил означает, что существует такая последовательность, подача которой на вход автомата, находящегося в различных состояниях из множества  , вызывает одинаковые реакции автомата и переводит его в одно и то же состояние. Понятно, что в этом случае любое продолжение упомянутой входной последовательности заведомо не может привести к построению ДП и поэтому такое продолжение не имеет смысла. Что касается пунктов 3 и 4, то комментарии, данные к таким же пунктам в разделе 1.3, в полной мере относятся и к нашему случаю.
, вызывает одинаковые реакции автомата и переводит его в одно и то же состояние. Понятно, что в этом случае любое продолжение упомянутой входной последовательности заведомо не может привести к построению ДП и поэтому такое продолжение не имеет смысла. Что касается пунктов 3 и 4, то комментарии, данные к таким же пунктам в разделе 1.3, в полной мере относятся и к нашему случаю.
Из сказанного выше вытекает следующая процедура построения минимальной по весу ДП. Среди всех вершин ДД, являющихся листьями, которым соответствуют простые  -группы состояний рассматриваемого автомата, отыскивается вершина
-группы состояний рассматриваемого автомата, отыскивается вершина  с минимальным значением
с минимальным значением 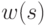 флажка. Входная последовательность, соответствующая пути из корня ДД в вершину
флажка. Входная последовательность, соответствующая пути из корня ДД в вершину  , и является ДП с минимальным весом, равным
, и является ДП с минимальным весом, равным 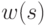 .
.
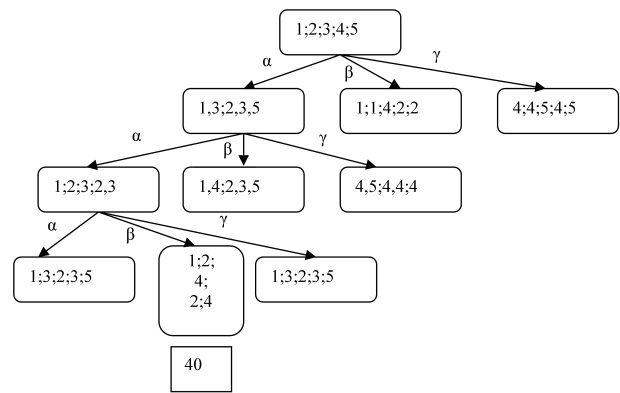
Проиллюстрируем процесс построения ДП для автомата, заданного табл. 1.1, полагая множество состояний  и веса символов входного алфавита теми же, что и в примере предыдущего раздела 1.3. ДД для этого автомата изображено на рис.1.3.
и веса символов входного алфавита теми же, что и в примере предыдущего раздела 1.3. ДД для этого автомата изображено на рис.1.3.
Из этого рисунка видно, что все вершины ДД, кроме вершины третьего уровня 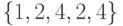 со значением флажка, равным 40, являются листьями в силу пункта 2 правил, приведенных выше, поскольку они содержат кратные
со значением флажка, равным 40, являются листьями в силу пункта 2 правил, приведенных выше, поскольку они содержат кратные  -множества. Единственная вершина - лист
-множества. Единственная вершина - лист 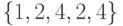 - является простой, и потому входная последовательность
- является простой, и потому входная последовательность  , соответствующая пути из корня ДД в эту вершину, является минимальной ДП, имеющей вес, равный 40.
, соответствующая пути из корня ДД в эту вершину, является минимальной ДП, имеющей вес, равный 40.
Заметим, что та же входная последовательность является одновременно минимальной и по длине.
Вопросы и упражнения
- Дайте определение автомата Мили.
- Что означает "взвешенность" входного алфавита автомата?
- Что такое эксперимент с автоматом?
- Приведите классификацию экспериментов с автоматами.
- Дайте определения синхронизирующих, установочных и диагностических последовательностей и поясните их содержательный смысл.
- Опишите структуру дерева преемников для автомата со взвешенным входным алфавитом.
- Каковы правила обрыва ветвей в дереве преемников при построении синхронизирующего (установочного, диагностического) дерева?
- Опишите процедуру построения минимальной по весу синхронизирующей (установочной, диагностической) последовательности с использованием конструкции синхронизирующего (установочного, диагностического) дерева.
-
Для автомата, заданного приведенной ниже таблицей переходов-выходов, постройте минимальную по весу синхронизирующую последовательность, если
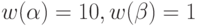 и множество допустимых начальных состояний есть
и множество допустимых начальных состояний есть 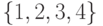 .
. - Для автомата из предыдущего упражнения постройте УП с минимальным весом, если
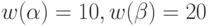 и множество допустимых начальных состояний есть
и множество допустимых начальных состояний есть 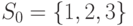 .
. - Для автомата из упражнения 9 постройте ДП с минимальным весом, если
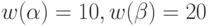 и множество
и множество 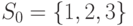 .
.