| Россия |
Эксперименты с билинейными автоматами по распознаванию состояний
Перейдем теперь к описанию используемой нами модели БА. Условимся, что для входных и выходных символов БА, а также для состояний БА будут сохранены те же обозначения, что и для ЛА.
Предполагается, что БА  задан над полем
задан над полем 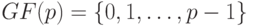 . Пространство состояний БА будем обозначать через
. Пространство состояний БА будем обозначать через 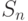 , где
, где  , а число
, а число  будем, как и в случае ЛА, называть размерностью БА.
будем, как и в случае ЛА, называть размерностью БА.
Далее рассматриваются БА, функционирование которых описывается следующими системами уравнений состояний и выходов соответственно:
 |
( 21.1) |
 |
( 21.2) |
где  - матрицы размерности
- матрицы размерности  - размерности
- размерности 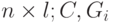 - размерности
- размерности 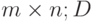 - размерности
- размерности  .
.
Упомянутые матрицы будем называть далее характеристическими матрицами БА. Элементами всех этих матриц являются элементы поля  .
.
Введем следующие обозначения:
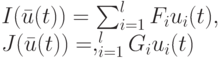
Пусть задана входная последовательность 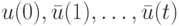 и пусть
и пусть  есть начальное состояние БА. Методом математической индукции можно доказать, что конечное состояние БА и его реакция вычисляются соответственно по формулам
есть начальное состояние БА. Методом математической индукции можно доказать, что конечное состояние БА и его реакция вычисляются соответственно по формулам
![\bar s(t+1)=\left ( \prod_{i=0}^{t}[A+I(t-i))] \right ) \bar s(0)+\left ( \prod_{i=0}^t [A+I(\bar u(t-1))\right )B\bar u(0) \dots +[A+I(\bar u(t))]B\bar u(t-1)+B\bar u(t)](/sites/default/files/tex_cache/7a51aa7517001e11484d47ae1ced4cda.png) |
( 21.3) |
![y(t)=([C+J(\bar u(t))]) \left (\prod_{i=0}^t[A+I(t-i-1))] \right ) \bar s(0)+[C+J(\bar u(t))]*\\
\|Pi_{i=0}^t[A+J(\bar u(t-1))]B\bar u(0)+ \dots +[C+J(\bar u(t))]B\bar u(t-1)+D\bar u(t)](/sites/default/files/tex_cache/0cd543b68b8bcab59b5471d2d4713dd3.png) |
( 21.4) |
Синхронизирующие последовательности
Применительно к БА  определение 1.1 СП
определение 1.1 СП 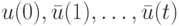 (в лекции 1) принимает следующий вид:
(в лекции 1) принимает следующий вид:
![\forall \bar s_1, \bar s_2 \in S_n \left \{ \prod_{i=0}^t[A+I(\bar u(t-i))]\bar s_1+\prod_{i=0}^t[A+I(\bar u(t-i))]B\bar u(0)+ \dots](/sites/default/files/tex_cache/bef5bf09d01390ac4e5774f21a50ecd1.png) |
( 21.5) |
![+[A+I(\bar u(t))]B\bar u(t-1)+B\bar u(t) \right \}=\left \{\prod_{i=0}^t[A+I(\bar u(t-i))] \bar s_2+](/sites/default/files/tex_cache/cc9c9e1cde4af2268fe9e89e9842ce66.png)
![+[A+I(\bar u(t))]B\bar u(t-1)+B\bar u(t) \right \}=\left { \prod_{i=0}^t[A+I(\bar u(t-i))]\bar s_2+](/sites/default/files/tex_cache/9e66356d74a992bdabc9bf4d8e535fe8.png)
![+\prod_{i=0}^{t-1}[A+I(\bar u(t-i))]B\bar u(0)_+\dots +[A+I(\bar u(t))]B\bar u(t-1)+B\bar u(k) \right \}](/sites/default/files/tex_cache/e5528d21df0b89eee8bc301627bcd8fb.png)
Перенося в левую часть равенства (21.5) все выражения, стоящие в правой его части, получим
![\forall \bar s \ne [0], |pi_{i=0}^t[A+I(\bar u(t-i))]\bar s=[0]](/sites/default/files/tex_cache/5e4cef22675ad7787d3fd806d3629766.png) |
( 21.6) |
где ![[0]](/sites/default/files/tex_cache/8d5162ca104fa7e79fe80fd92bb657fb.png) - нулевая матрица (в частности, вектор) соответствующей размерности.
- нулевая матрица (в частности, вектор) соответствующей размерности.
Теорема 21.1. Для того чтобы входная последовательность 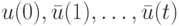 была СП для БА
была СП для БА  , необходимо и достаточно, чтобы выполнялось равенство
, необходимо и достаточно, чтобы выполнялось равенство
![\prod_{i=0}^t[A+I(\bar u(t-i))]=[0]](/sites/default/files/tex_cache/e193eb01a791234335c6f4a9ab9f3c5a.png) |
( 21.7) |
Доказательство. Докажем необходимость условия (21.7), поскольку его достаточность очевидна. Обозначим через ![H=[h_{ij}]](/sites/default/files/tex_cache/7cbaabb742771056fb59222b53796795.png) матрицу, представляющую собой левую часть (21.7). Пусть
матрицу, представляющую собой левую часть (21.7). Пусть 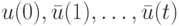 есть СП, но тогда выполняется равенство (21.6). Поскольку
есть СП, но тогда выполняется равенство (21.6). Поскольку  - произвольное состояние, то положим
- произвольное состояние, то положим ![\bar s=[1,0,\dots ,0]'](/sites/default/files/tex_cache/8859da1a48380900f17ce32cf788b9bb.png) , при котором (21.6) становится равенством
, при котором (21.6) становится равенством ![[h_{11} h_{21} \dots h_{n1}]'=[0]](/sites/default/files/tex_cache/c743121480c796912a484905d6bb7bc0.png) . Из этого равенства следует, что
. Из этого равенства следует, что  . Полагая далее
. Полагая далее  равным векторам
равным векторам ![[0,1,0,\dots , 0]', \dots, [0, 0, \dots, 1]'](/sites/default/files/tex_cache/1abded93002e99988a84c06fec5e265d.png) , аналогичными рассуждениями придем к заключению, что и все остальные столбцы матрицы
, аналогичными рассуждениями придем к заключению, что и все остальные столбцы матрицы  , как и ее первый столбец, нулевые. Таким образом, из (21.6) следует (21.7), что и требовалось доказать.
, как и ее первый столбец, нулевые. Таким образом, из (21.6) следует (21.7), что и требовалось доказать.
Из (21.7) следует справедливость следующего утверждения.
Теорема 21.2. Для того чтобы входная последовательность 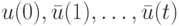 была СП для БС
была СП для БС  , достаточно, чтобы по крайней мере для одного из значений
, достаточно, чтобы по крайней мере для одного из значений 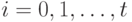 выполнялось равенство
выполнялось равенство
![[A+I(\bar u(t-i))]=[0]](/sites/default/files/tex_cache/76ae19c886d8eb66c97d2d26697eecde.png) |
( 21.8) |
Приведем еще одно достаточное условие существования СП. Предварительно напомним, что квадратная матрица называется верхней (нижней) треугольной, если все ее элементы, лежащие на главной диагонали и ниже (выше) ее, нулевые.
Теорема 21.3. Если характеристические матрицы  и
и 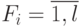 , БС
, БС  являются верхними (нижними) треугольными, то для этой БС существуют СП длины, не большей
являются верхними (нижними) треугольными, то для этой БС существуют СП длины, не большей  , где
, где  - число строк и столбцов упомянутых матриц.
- число строк и столбцов упомянутых матриц.
Доказательство. Пусть  и
и 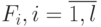 , являются верхними треугольными матрицами. Тогда каждый сомножитель в произведении (21.7) также представляет собой матрицу того же типа. Условимся нумеровать диагонали этих матриц, лежащие выше главной диагонали и параллельные ей, числами
, являются верхними треугольными матрицами. Тогда каждый сомножитель в произведении (21.7) также представляет собой матрицу того же типа. Условимся нумеровать диагонали этих матриц, лежащие выше главной диагонали и параллельные ей, числами 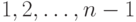 . Непосредственными вычислениями легко убедиться, что все элементы первой диагонали матрицы-произведения двух верхних треугольных матриц равны нулю. Если эту матрицу вновь умножить на верхнюю треугольную матрицу, т. е. взять произведение трех сомножителей из (21.7), то в результате получится матрица, у которой нулевыми будут элементы первой и второй диагонали. Отсюда методом индукции можно доказать, что произведение
. Непосредственными вычислениями легко убедиться, что все элементы первой диагонали матрицы-произведения двух верхних треугольных матриц равны нулю. Если эту матрицу вновь умножить на верхнюю треугольную матрицу, т. е. взять произведение трех сомножителей из (21.7), то в результате получится матрица, у которой нулевыми будут элементы первой и второй диагонали. Отсюда методом индукции можно доказать, что произведение  штук верхних треугольных матриц даст нулевую матрицу. Тогда на основании теоремы 21.1 рассматриваемая БА имеет СП, длина которой не превосходит
штук верхних треугольных матриц даст нулевую матрицу. Тогда на основании теоремы 21.1 рассматриваемая БА имеет СП, длина которой не превосходит  .
.
Для нижних треугольных матриц соответствующее утверждение доказывается аналогично.
Поскольку БА представляет собой автомат Мили, для построения для нее УП (в частности, СП) и ДП применимы известные методы, описанные в [18], которые, однако, достаточно трудоемки, так как базируются на использовании конструкции дерева преемников. Ниже описываются аналитические методы построения различных типов последовательностей для БА, менее трудоемкие, чем методы из [18].
Опишем метод построения СП. Обратимся к равенству (21.7) и на его основе организуем пошаговый процесс поиска СП, начиная с СП длины 1 (при 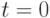 ), затем СП длины 2 (при
), затем СП длины 2 (при 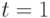 ) и т. д. При варьировании величины
) и т. д. При варьировании величины  равенство (21.7) будет принимать последовательно следующий вид:
равенство (21.7) будет принимать последовательно следующий вид:
![A+I(\bar u(0))=[0],\\
[A+I(\bar u(1))][A+I(\bar u(0))]=[0],\\
………………………………………,\\
[A+I(\bar u(t-1))][A+I(\bar u(t-2))] \dots [A+I(\bar u(0))]=[0]](/sites/default/files/tex_cache/35a71b400f957dacd7693b0be416df76.png) |
( 21.9) |
Поиск СП начнем с попытки решения первой из выписанных систем в (21.9), рассматривая в качестве неизвестных координаты вектора  . Эта неоднородная система линейных уравнений
. Эта неоднородная система линейных уравнений 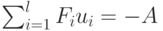 имеет следующую матрицу:
имеет следующую матрицу:
![L=
\left [
\begin {matrix}
f_{11}(1)& f_{11}(2)& \dots& f_{11}(l)\\
\dots & \dots &\dots &\dots\\
f_{nn}(1)& f_{nn}(2)& \dots &f_{nn}(l)
\end {matrix}
\right ]](/sites/default/files/tex_cache/6faa2c3300da668f6c31588ad0c342d3.png)
Здесь элементы 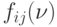 есть элементы матрицы
есть элементы матрицы  . Как известно [19], эта система будет совместной, если
. Как известно [19], эта система будет совместной, если 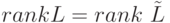 , где
, где 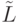 - расширенная (добавлением столбца, состоящего из соответствующих элементов матрицы
- расширенная (добавлением столбца, состоящего из соответствующих элементов матрицы  ) матрица той же системы. В случае совместности этой системы возможны два случая: 1)
) матрица той же системы. В случае совместности этой системы возможны два случая: 1) 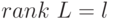 ; 2)
; 2)  . В первом случае система имеет единственное решение, которое дает искомую СП. Во втором случае система имеет множество решений, каждому из которых соответствует своя СП. Поскольку решение системы отыскивается среди элементов конечного поля
. В первом случае система имеет единственное решение, которое дает искомую СП. Во втором случае система имеет множество решений, каждому из которых соответствует своя СП. Поскольку решение системы отыскивается среди элементов конечного поля  , множество решений будет конечным.
, множество решений будет конечным.
Если упомянутая система линейных уравнений окажется несовместной, то перейдем к рассмотрению следующей системы в (21.9) и так до тех пор, пока либо очередная система не окажется совместной, либо параметр  не достигнет значения
не достигнет значения  , где
, где  - число состояний рассматриваемой БА. Если и при предельном значении
- число состояний рассматриваемой БА. Если и при предельном значении  СП не будет найдена, то для этой БА ее не существует, поскольку упомянутое значение есть верхняя граница длины СП. Отметим, что все системы в (21.9) начиная со второй являются нелинейными. Для таких систем не существует общих методов решения, однако в силу конечности поля
СП не будет найдена, то для этой БА ее не существует, поскольку упомянутое значение есть верхняя граница длины СП. Отметим, что все системы в (21.9) начиная со второй являются нелинейными. Для таких систем не существует общих методов решения, однако в силу конечности поля  , над которым рассматриваются такие системы, решение может быть найдено либо перебором, либо с помощью некоторого частного метода, который может быть предложен с учетом специфики конкретной системы.
, над которым рассматриваются такие системы, решение может быть найдено либо перебором, либо с помощью некоторого частного метода, который может быть предложен с учетом специфики конкретной системы.
Проиллюстрируем метод на примере БА над полем  , у которой
, у которой  , а характеристические матрицы имеют следующий вид:
, а характеристические матрицы имеют следующий вид:
![A=
\left [
\begin {matrix}
1&0&0\\
0&0&0\\
0&0&0
\end {matrix}
\right ] ,
F_i=
\left [
\begin {matrix}
0&0&1\\
0&1&0\\
0&0&0
\end {matrix}
\right ],
F_2=
\left [
\begin {matrix}
0&0&1\\
0&0&0\\
1&0&1
\end {matrix}
\right ]](/sites/default/files/tex_cache/6a7e8aba41373b9e2b135f49793fc68d.png)
Первое равенство в (21.9) дает следующую систему уравнений:
![\left [
\begin {matrix}
1&0&0\\
0&0&0\\
0&0&0
\end {matrix}
\right ] +
\left [
\begin {matrix}
0&0&1\\
0&1&0\\
0&0&0
\end {matrix}
\right ] u_1(0)+
\left [
\begin {matrix}
0&0&1\\
0&0&0\\
1&0&1
\end {matrix}
\right ] u_2(0)=
\left [
\begin {matrix}
0&0&0\\
0&0&0\\
0&0&0
\end {matrix}
\right ]](/sites/default/files/tex_cache/24d9c426953db0930ed91276dc0def01.png)
Легко убедиться, что она несовместна, и потому выписываем вторую систему из (21.9):
![\left (
\left [
\begin {matrix}
1&0&0\\
0&0&0\\
0&0&0
\end {matrix}
\right ]+
\left [
\begin {matrix}
0&0&1\\
0&1&0\\
0&0&0
\end {matrix}
\right ] u_1(0)+
\left [
\begin {matrix}
0&0&1\\
0&0&0\\
1&0&0
\end {matrix}
\right ]u_2(0)
\right) \cdot\\
\cdot \left (
\left [
\begin {matrix}
1&0&0\\
0&0&0\\
0&0&0
\end {matrix}
\right ]+
\left [
\begin {matrix}
0&0&1\\
0&1&0\\
0&0&0
\end {matrix}
\right ]u_1(1)+
\left [
\begin {matrix}
0&0&1\\
0&0&0\\
1&0&0
\end {matrix}
\right ]u_2(1)
\right )=
\left [
\begin {matrix}
0&0&0\\
0&0&0\\
0&0&0
\end {matrix}
\right ]](/sites/default/files/tex_cache/db1ab8e608da9e188559e8ccb7f405af.png)
После выполнения преобразований система примет вид
![\left [
\begin {matrix}
1+(u_1(0)+u_2(0))u_2(1)& 0& u_1(1)+u_2(1)+u_2(1)(u_1(0)+u_2(0))\\
0&u_1(0)u_1(1)&0\\
u_2(0)+u_2(0)u_2(1)&0&u_2(0)(u_1(1)+u_2(1))+u_2(0)u_2(1)
\end {matrix}
\right ] =[0]](/sites/default/files/tex_cache/2305b68d1a3ce976dd718af4824aded6.png)
В конечном счете, приравнивая каждый элемент последней матрицы нулю, получим систему уравнений
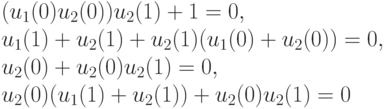
Напомним, что решение мы ищем в поле  и потому операция "+" - это сложение по модулю 2. Легко убедиться, что эта система имеет два решения:
и потому операция "+" - это сложение по модулю 2. Легко убедиться, что эта система имеет два решения:
-
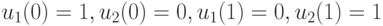 ;
; -
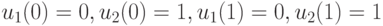 .
.
Таким образом, рассматриваемый БА имеет две СП: ![\bar u(0)=[1,0]', \bar u(1)=[0,1]'](/sites/default/files/tex_cache/67ef4c007a5d03eff9b82592d5de0b6f.png) и
и ![\bar u(0)=[0,1]', \bar u(1)=[0,1]'](/sites/default/files/tex_cache/13ab402ba4718e9306fa97d83ad0198a.png) .
.
Задачи синхронизации и установки автоматов - это разновидности задачи управления дискретной системой (ДС), которая в общем виде формулируется следующим образом: для рассматриваемой ДС найти такую входную последовательность, которая переводит ее из состояния  в состояние
в состояние  . Для автоматов, заданных графом переходов, эта задача сводится к задаче поиска путей на графе между двумя заданными вершинами, методы решения которой известны. Однако для автоматов с большим числом состояний проблема построения графа переходов сама по себе является трудоемкой. Покажем, что для БА может быть предложен аналитический метод решения упомянутой задачи, не требующий знания графа переходов.
. Для автоматов, заданных графом переходов, эта задача сводится к задаче поиска путей на графе между двумя заданными вершинами, методы решения которой известны. Однако для автоматов с большим числом состояний проблема построения графа переходов сама по себе является трудоемкой. Покажем, что для БА может быть предложен аналитический метод решения упомянутой задачи, не требующий знания графа переходов.
Поиск требуемой входной последовательности осуществим следующим образом. В (21.1) положим 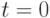 и вместо
и вместо  подставим состояние
подставим состояние  , а вместо
, а вместо 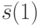 - состояние
- состояние  . Полученное выражение будем рассматривать как систему линейных алгебраических уравнений относительно неизвестных
. Полученное выражение будем рассматривать как систему линейных алгебраических уравнений относительно неизвестных 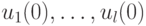 . Очевидно, что если эта система совместна, то ее решению соответствует искомая входная последовательность. Если таких решений будет несколько, то это говорит о существовании нескольких путей перехода из
. Очевидно, что если эта система совместна, то ее решению соответствует искомая входная последовательность. Если таких решений будет несколько, то это говорит о существовании нескольких путей перехода из 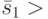 в
в  , а отсутствие решений - о невозможности требуемого перехода с помощью входной последовательности длины 1. В последнем случае сделаем попытку найти соответствующую последовательность длины 2, положив в (21.3)
, а отсутствие решений - о невозможности требуемого перехода с помощью входной последовательности длины 1. В последнем случае сделаем попытку найти соответствующую последовательность длины 2, положив в (21.3) 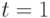 и заменив
и заменив  и
и 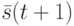 соответственно на
соответственно на  и
и  . Если полученная система вновь окажется несовместной, то продолжим описанный процесс далее аналогичным образом. Если до значения
. Если полученная система вновь окажется несовместной, то продолжим описанный процесс далее аналогичным образом. Если до значения 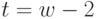 включительно, где
включительно, где  - число состояний БА, все последовательно получаемые системы линейных уравнений окажутся несовместными, то это означает, что переход из
- число состояний БА, все последовательно получаемые системы линейных уравнений окажутся несовместными, то это означает, что переход из  в
в  невозможен, поскольку если соответствующий путь существует, то длина его не может превосходить
невозможен, поскольку если соответствующий путь существует, то длина его не может превосходить  .
.
Проиллюстрируем описанный метод на примере БА над полем  , уже рассмотренном выше, где характеристическая матрица
, уже рассмотренном выше, где характеристическая матрица  имеет вид
имеет вид
![B=
\left [
\begin {matrix}
1&0\\
0&1\\
1&0
\end {matrix}
\right ]](/sites/default/files/tex_cache/88cd4767447ad7c96124fae4be950a61.png)
Пусть требуется найти входную последовательность, переводящую заданную БС из состояния ![\bar s_1=[1,1,1]'](/sites/default/files/tex_cache/24d27ac24a8f747669c839a3233f8ad4.png) в состояние
в состояние ![\bar s_2=[0,0,1]'](/sites/default/files/tex_cache/434b4ee167eabf873bcd267d961199e4.png) .
.
Выпишем систему уравнений, используя выражение (6.1):
![\left [
\begin {matrix}
1&0&0\\
0&0&0\\
0&0&0
\end {matrix}
\right ]\times
\left [
\begin {matrix}
1\\
1\\
1
\end {matrix}
\right ] +
\left (
\left [
\begin {matrix}
0&0&1\\
0&1&0\\
0&0&0
\end {matrix}
\right ] u_1(0)+
\left [
\begin {matrix}
0&0&1\\
0&0&0\\
1&0&1
\end {matrix}
\right ] u_2(0)
\right )
+ \left [
\begin {matrix}
1&0\\
0&1\\
1&0
\end {matrix}
\right ] \times
\left [
\begin {matrix}
u_1(0)\\
u_2(0)
\end {matrix}
\right ] =
\left [
\begin {matrix}
0\\
0\\
1
\end {matrix}
\right ]](/sites/default/files/tex_cache/a6bb3f4a52bc99dc61417c9e8141e033.png)
Выполнив соответствующие преобразования, в итоге получим систему
![\left [
\begin {matrix}
u_2(0)+1\\
u_1(0)+u_2(0)\\
u_1(0)
\end {matrix}
\right ]=
\left [
\begin {matrix}
0\\
0\\
1
\end {matrix}
\right ]](/sites/default/files/tex_cache/b844d864f9adcb9a9b445fb606119410.png)
Эта система имеет единственное решение 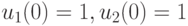 , следовательно, искомая входная последовательность есть
, следовательно, искомая входная последовательность есть ![[1,1]'](/sites/default/files/tex_cache/3ab3ad06256726cbc8f4c0f58410db66.png) .
.
