| Россия |
Эксперименты с автоматами, имеющими взвешенный входной алфавит
Основные определения
Введем некоторые основные понятия теории автоматов, которые используются в дальнейшем изложении.
Под автоматом Мили будем понимать пятерку 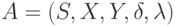 , где
, где 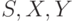 - конечные множества состояний, входной и выходной алфавиты соответственно,
- конечные множества состояний, входной и выходной алфавиты соответственно,  и
и  - функции переходов и выходов, задающие отображения
- функции переходов и выходов, задающие отображения 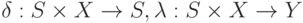 , . Через
, . Через  обозначим подмножество множества состояний
обозначим подмножество множества состояний  , которое назовем множеством допустимых начальных состояний автомата
, которое назовем множеством допустимых начальных состояний автомата  .
.
Предполагается, что множества  и
и  автомата
автомата  конечны (такие автоматы называются конечными).
конечны (такие автоматы называются конечными).
Через 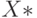 обозначим множество всех последовательностей (слов) конечной длины в алфавите
обозначим множество всех последовательностей (слов) конечной длины в алфавите  . Через
. Через  обозначим пустое слово (нулевой длины) в любом алфавите. Полагаем, что
обозначим пустое слово (нулевой длины) в любом алфавите. Полагаем, что  . Распространим функции переходов и выходов автомата на множество
. Распространим функции переходов и выходов автомата на множество 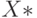 следующим образом:
следующим образом:
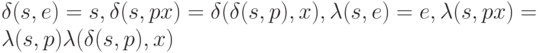
где 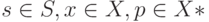 . Последовательность выходов автомата
. Последовательность выходов автомата 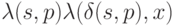 получена с помощью операции конкатенации (приписывания) двух слов:
получена с помощью операции конкатенации (приписывания) двух слов: 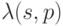 и
и 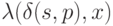 .
.
Автомат Мили  может быть задан в виде таблиц переходов и выходов (иногда они совмещаются в одну таблицу), с помощью матриц и, наконец, с помощью графа. Форма представления автомата в виде графа является наиболее наглядной. В дальнейшем изложении мы будем пользоваться в основном графовой и табличной формами представления автомата, которые подробно описаны в [18]. Напомним, что множеством вершин графа переходов автомата
может быть задан в виде таблиц переходов и выходов (иногда они совмещаются в одну таблицу), с помощью матриц и, наконец, с помощью графа. Форма представления автомата в виде графа является наиболее наглядной. В дальнейшем изложении мы будем пользоваться в основном графовой и табличной формами представления автомата, которые подробно описаны в [18]. Напомним, что множеством вершин графа переходов автомата  являются состояния из
являются состояния из  , а множество дуг есть совокупность четверок
, а множество дуг есть совокупность четверок 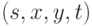 , где
, где 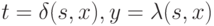 . Пара
. Пара  называется отметкой дуги,
называется отметкой дуги,  - ее началом,
- ее началом,  - концом.
- концом.
Пусть 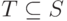 , тогда полагаем, что
, тогда полагаем, что  и
и  , где объединение выполняется по всем
, где объединение выполняется по всем  .
.
Состояние  назовем достижимым из
назовем достижимым из  , если
, если 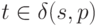 для некоторого
для некоторого 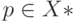 .
.
Автомат  назовем сильно связным, если его граф переходов сильно связен, т. е. из любого состояния автомата достижимы все его состояния. Состояние
назовем сильно связным, если его граф переходов сильно связен, т. е. из любого состояния автомата достижимы все его состояния. Состояние  называется преходящим в автомате
называется преходящим в автомате  , если
, если  не является концом ни одной дуги автомата, т. е.
не является концом ни одной дуги автомата, т. е.  не достижимо ни из одного состояния, отличного от
не достижимо ни из одного состояния, отличного от  . Состояние
. Состояние  называется тупиковым в автомате
называется тупиковым в автомате  , если из
, если из  не достижимо ни одно состояние, отличное от
не достижимо ни одно состояние, отличное от  .
.
Каждому входному символу  из алфавита
из алфавита  автомата
автомата  поставим в соответствие некоторое положительное число
поставим в соответствие некоторое положительное число 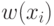 и назовем его весом символа
и назовем его весом символа  . Далее такой алфавит будем называть взвешенным. Весом входной последовательности
. Далее такой алфавит будем называть взвешенным. Весом входной последовательности 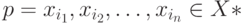 назовем число
назовем число

Следуя традиции классической теории экспериментов с автоматами, будем различать безусловные и условные эксперименты [18]. Безусловный эксперимент предполагает подачу на вход автомата такой последовательности, которая определена заранее, т. е. до начала эксперимента. При проведении условного эксперимента на вход автомата подается две или более подпоследовательности, причем каждая последующая подпоследовательность, кроме первой, формируется на основании реакций, вызываемых предыдущими подпоследовательностями.
Преимущества условных экспериментов состоят в том, что они, во-первых, иногда могут оказаться короче безусловных и, во-вторых, в некоторых случаях их строить легче, чем безусловные.
Один автомат будем называть копией другого, если они имеет одинаковые графы переходов и перед началом эксперимента оба они находятся в одном и том же состоянии. По числу требуемых для эксперимента копий автомата различают простые, когда требуется лишь один экземпляр автомата, и кратные эксперименты, когда требуется более чем один экземпляр автомата.
В дальнейшем изложении мы в основном будем иметь дело с простыми безусловными экспериментами.
В классической теории экспериментов с автоматами были исследованы две задачи, получившие наименование диагностической и установочной. В обеих задачах предполагается известным автомат, т. е., например, его граф переходов, и множество  его допустимых начальных состояний, т. е. истинное начальное (стартовое) состояние. Это состояние есть одно из состояний множества
его допустимых начальных состояний, т. е. истинное начальное (стартовое) состояние. Это состояние есть одно из состояний множества  . Диагностическая задача состоит в отыскании начального (стартового) состояния заданного автомата, а установочная - в установке автомата в известное состояние. Эксперименты, решающие перечисленные задачи, принято называть диагностическими и установочными соответственно. Интерес к этим задачам объясняется возможностью приложений результатов их решения к контролю и диагностике реальных цифровых устройств.
. Диагностическая задача состоит в отыскании начального (стартового) состояния заданного автомата, а установочная - в установке автомата в известное состояние. Эксперименты, решающие перечисленные задачи, принято называть диагностическими и установочными соответственно. Интерес к этим задачам объясняется возможностью приложений результатов их решения к контролю и диагностике реальных цифровых устройств.
Проведение установочных и диагностических экспериментов с автоматами требует наличия специальных входных последовательностей, которые мы также будем именовать установочными (УП) и диагностическими (ДП) последовательностями соответственно.
Дадим теперь формальные определения этих последовательностей. Входная последовательность 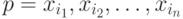 называется установочной последовательностью для автомата
называется установочной последовательностью для автомата  и множества
и множества  его допустимых начальных состояний, если
его допустимых начальных состояний, если
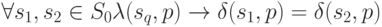 |
( 1.1) |
Содержательно это определение означает, что по наблюдаемой реакции на УП автомата  , находящегося в неизвестном для наблюдателя начальном состоянии, всегда однозначно можно определить его конечное состояние.
, находящегося в неизвестном для наблюдателя начальном состоянии, всегда однозначно можно определить его конечное состояние.
Входная последовательность 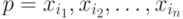 называется диагностической последовательностью для автомата
называется диагностической последовательностью для автомата  и множества
и множества  его допустимых начальных состояний, если
его допустимых начальных состояний, если
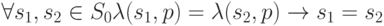 |
( 1.2) |
Содержательно это определение означает, что по наблюдаемой реакции на ДП автомата  , находящегося в неизвестном для наблюдателя начальном состоянии, всегда однозначно можно определить это начальное (стартовое) состояние.
, находящегося в неизвестном для наблюдателя начальном состоянии, всегда однозначно можно определить это начальное (стартовое) состояние.
Определим еще один тип последовательности, которую назовем синхронизирующей (СП). Входная последовательность 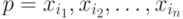 называется синхронизирующей последовательностью для автомата
называется синхронизирующей последовательностью для автомата  и множества
и множества  его допустимых начальных состояний, если
его допустимых начальных состояний, если
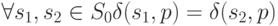 |
( 1.3) |
Содержательно это определение означает, что после подачи на автомат  СП этот автомат оказывается в одном и том же известном наблюдателю конечном состоянии независимо от того, из какого начального состояния он стартовал.
СП этот автомат оказывается в одном и том же известном наблюдателю конечном состоянии независимо от того, из какого начального состояния он стартовал.
Очевидно, что СП по существу является УП, поскольку после ее подачи автомат оказывается в известном состоянии, хотя никакого наблюдения реакций производить не нужно. Другими словами, подачу на вход автомата СП можно трактовать как синхронизирующий эксперимент, но эксперимент "вырожденный", поскольку он не требует наблюдения реакции автомата.
Ниже мы займемся разработкой методов построения СП, УП и ДП в предположении, что автомат  имеет взвешенный входной алфавит
имеет взвешенный входной алфавит  . При этом нас будут интересовать все три типа последовательностей с минимальным весом. Как уже было упомянуто выше, известные ранее методы построения минимальных по длине последовательностей, описанные в [18], в рассматриваемой ситуации оказываются непригодными. Вместе с тем базисная конструкция дерева преемников, использованная в [18] для синтеза УП и ДП, минимальных по длине, оказывается вполне работоспособной и в нашем случае, однако она, что вполне естественно, требует соответствующих изменений.
. При этом нас будут интересовать все три типа последовательностей с минимальным весом. Как уже было упомянуто выше, известные ранее методы построения минимальных по длине последовательностей, описанные в [18], в рассматриваемой ситуации оказываются непригодными. Вместе с тем базисная конструкция дерева преемников, использованная в [18] для синтеза УП и ДП, минимальных по длине, оказывается вполне работоспособной и в нашем случае, однако она, что вполне естественно, требует соответствующих изменений.
Понятно, что, располагая методами построения минимальных по весу СП, УП и ДП для автоматов со взвешенным входным алфавитом, всегда можно построить соответствующие последовательности, минимальные по длине, положив вес каждого символа алфавита  равным единице. Таким образом, описываемые ниже методы построения упомянутых последовательностей являются более общими, чем известные ранее.
равным единице. Таким образом, описываемые ниже методы построения упомянутых последовательностей являются более общими, чем известные ранее.
Заметим, что в этой лекции мы не касаемся вопросов существования упомянутых выше трех типов последовательностей, поскольку для автоматов Мили они подробно отражены в [18]. Легко сообразить, что "взвешенность" алфавита никак не влияет на условия существования соответствующих последовательностей.
