|
При попытке сдать тест 7 система попросила повторную авторизацию, после которой все достижения исчезли и теперь заново предлагается пройти курс. Как восстановить ход обучения? |
Организационный инструментарий менеджмента
4.3. Сетевые матрицы
Общее представление о коридорных сетевых графиках
В так называемых коридорных сетевых графиках в качестве коридора может приниматься часть всего комплекса работ или же отдельных исполнительских работ ( рис. 4.12).
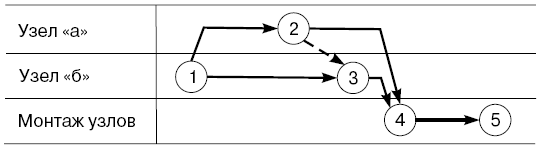
Принадлежность работы к тому или иному коридору определяется ее горизонтальным положением (или отрезком) в этом коридоре, как это показано на рис. 4.13.
Так, на рисунке видим, что работы 1-2 и 2-4 выполняются по узлу "а", так как горизонтальные отрезки этих работ лежат в плоскости коридора узла "а". Работы 1-3 и 3-4 выполняются по узлу "б", так как горизонтальные отрезки этих работ лежат в плоскости коридора узла "б".
На рис. 4.14 показаны те же работы, но уже в разрезе (в коридорах) исполнителей работ. Работы 1-2 и 2-4 выполняются главным инженером, работы 1-3 и 3-4 - генеральным директором, а работа 4-5 - коммерческим директором.
Иногда наглядность коридорного графика можно значительно увеличить, показав на нем одновременно сами работы и их исполнителей. Для этого вместо графического изображения события кружком примем совершенно различные фигуры для изображения событий, являющихся начальными событиями работ, выполняемых различными исполнителями ( рис. 4.15).
Так, Исполнитель 1 на графике изображен треугольником. Исполнитель 2 обозначается квадратом. Исполнитель 3 обозначается кружком. Таким образом, любая фигура, стоящая в начале работы, обозначает конкретного исполнителя этой работы. Так, работу 1-2 по узлу "а" выполняет Исполнитель 1. Работу 3-4 по узлу "б" выполняет Исполнитель 2, и т.д.
Как видно, коридорный сетевой график несет значительно больше информации, чем обычный сетевой. Это качество позволяет использовать его в тех случаях, когда простого сетевого графика бывает недостаточно для выполнения функций менеджмента.
Сетевая матрица
Сетевая матрица представляет собой коридорно-масштабный сетевой график, организованный в разрезе исполнителей работ.
Сетевая матрица позволяет увязывать в единый комплексный инструмент логико-временную структуру и организационную структуру управления организации.
Применение сетевых матриц в процессе менеджмента проекта дает возможность представить этот процесс в наглядной форме, а также выявить особенности ситуации, структуру необходимых работ и приемлемые средства и методы их выполнения, проанализировать взаимосвязи между исполнителями и работой, подготовить научно обоснованный скоординированный план выполнения всего комплекса работ по решению поставленной задачи. Такой план позволяет более эффективно использовать имеющиеся ресурсы, так как анализ сетевой матрицы и определение критических работ и резервов времени на некритических работах дают возможность перераспределять ресурсы с целью лучшего использования и сокращения срока реализации поставленных задач. Появляется также возможность быстро обрабатывать с помощью средств вычислительной техники большие массивы отчетных данных и обеспечивать руководство фирмы своевременной и исчерпывающей информацией о фактическом состоянии работ, облегчающей корректировку принятых решений; прогнозировать ход выполнения работ на критическом пути и концентрировать на них внимание менеджеров различных уровней. Используя математический аппарат, можно определить степень вероятности реализации плана и правильно распределять ответственность по иерархическим ступеням менеджмента.
Сетевая матрица представляет собой графическое изображение процессов проектного менеджмента, где все операции, выполнение которых необходимо для достижения конечной цели, показаны в определенной технологической последовательности и взаимозависимости. Сетевая матрица совмещается с календарно-масштабной сеткой времени, которая имеет горизонтальные и вертикальные коридоры. Горизонтальные коридоры характеризуют ступень менеджмента, структурное подразделение или должностное лицо, выполняющие ту или иную операцию процесса подготовки, принятия и реализации решения; вертикальные - этап и отдельные операции процесса принятия решения, протекающие во времени.
Сетевая матрица является разновидностью сетевого графика. Поэтому при построении сетевой матрицы используются те же три основных понятия, что и при построении сетевых графиков:
- работа (включая ожидание и зависимость);
- событие;
- путь.
Все правила построения сетевых графиков распространяются также и на сетевые матрицы.
Построение сетевой матрицы
Для правильного построения сетевой матрицы помимо общих правил построения сетевых графиков следует придерживаться нескольких особенных правил, непосредственно касающихся сетевых матриц как коридорно-масштабной разновидности сетевых моделей.
Принадлежность работы (стрелки) к тому или иному горизонтальному коридору определяется ее горизонтальным положением либо ее безмасштабным горизонтальным участком в этом коридоре. Принадлежность работы (стрелки) к вертикальному коридору определяется вертикальными границами коридора, этапа или операции, т.е. вертикальными линиями, определяющими масштаб времени матрицы.
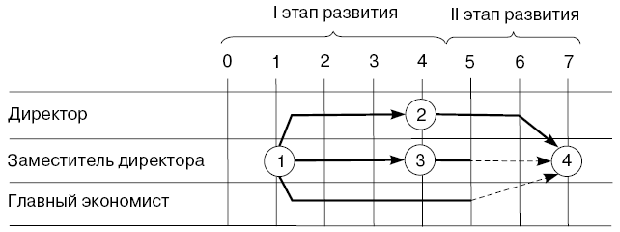
На рис. 4.16 представлен пример простейшей сетевой матрицы.
Из рисунка видно, что работы 1-2 и 2-4 выполняются директором, работы 1-3 и 3-4 - заместителем директора, работа 1-4 - главным экономистом. Работы 1-2 и 1-3 выполняются на I этапе решения; работы 2-4 и 3-4 - на II, а работа 1-4 - в течение I и II этапов.
Продолжительность каждой работы на сетевой матрице определяется расстоянием по сплошной линии между центрами двух событий, заключающих эту работу (стрелку) в проекции на горизонтальную ось времени. На рис. 4.16 работы 1-2 и 1-3 имеют продолжительность, равную четырем единицам времени. Местонахождение каждого события на сетевой матрице определяется окончанием наиболее удаленной вправо (на сетке времени) входящей в него стрелки. Все остальные менее удаленные вправо от оси ординат и входящие в это же событие стрелки соединяются с ним прерывистой (обычно либо штрих-пунктирной линией "точка-тире", либо волнистой линией) линией со стрелкой на конце.
Зависимость, идущая на матрице с наклоном вправо от оси ординат, изображается в виде разорванной прерывистой линии (обычно либо штрихпунктирной линией "точка-тире", либо разорванной волнистой линией) со стрелкой на конце. Зависимость, идущая по вертикали (ее проекция на горизонтальную ось времени - точка, а следовательно, продолжительность равна 0), изображается, как обычно, пунктирной стрелкой.
Длина волнистой линии показывает величину частного резерва времени. Например, работа 1-4 имеет частный резерв времени, равный двум единицам времени. Такой же резерв имеет работа 3-4.
В качестве примера рассмотрим небольшой абстрактный комплекс работ. В табл. 4.15 указана последовательность этих работ, продолжительность, а также система ответственности за выполнение работ.
| h-i | i-j | 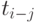 |
Исполнитель |
|---|---|---|---|
| - | А | 3 | ПЭО |
| - | Б | 4 | ТО |
| А | В | 4 | ПЭО |
| Б | Г | 6 | ТО |
| В | Д | 5 | ПЭО |
| - | Е | 7 | ОМТС |
| В, Е | Ж | 4 | ПЭО |
| ПЭО | - | планово-экономический отдел; |
| ТО | - | технический отдел; |
| ОМТС | - | отдел материально-технического снабжения |
Построим сетевую матрицу для указанного в табл. 4.15 комплекса работ.
Первым шагом будет построение коридорно-масштабной сетки, в рамках которой расположим в дальнейшем сетевой график. Количество горизонтальных коридоров будет соответствовать количеству исполнителей. В рассматриваемом примере их три - планово-экономический отдел (ПЭО), технический отдел (ТО), отдел материально-технического снабжения (ОМТС). В качестве единицы измерения времени целесообразно выбрать один день, так как продолжительность работ не очень большая.
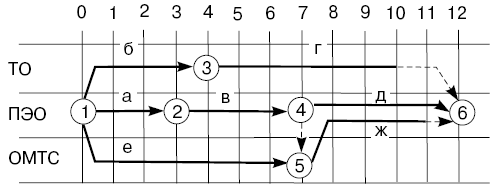
После этого начинаем построение сетевого графика в рамках созданной сетки матрицы. Работам А, Б и Е другие работы не предшествуют, поэтому они выходят из начального события. Работу А располагаем в коридоре ПЭО, работу Б - в коридоре ТО, а работу Е - в коридоре ОМТС. Работа В следует за работой А и располагается в том же, что и работа А, коридоре ПЭО. Работа Г следует за работой Б и располагается так же, как работа Г, - в коридоре ТО. Работа Д следует за работой В и находится в коридоре ПЭО. Для правильного отображения начала работы Ж необходимо ввести дополнительное событие и зависимость, так как если замкнуть работы В и Е одним событием, то не будет возможности отобразить зависимость работы Д только от работы В. За работами Г, Д и Ж никаких работ не следует, поэтому они сходятся в одном завершающем событии. Для правильного отображения продолжительности этих работ нужно учесть, что работа Д имеет самый поздний срок завершения - 12-й день. Отрезок от завершения работы Г до завершающего события, т.е. до 12-го дня, отображаем как штрихпунктирную линию частного резерва времени. Так же поступаем и с работой Ж. Частный резерв работы Г составляет два дня, а работы Ж - один день. В завершение проставляем номера событий.
В итоге получаем сетевую матрицу, изображенную на рис. 4.17.
После построения сетевой матрицы к ней можно применять все известные методы расчета аналитических параметров и оптимизации модели.