Генерация кода
Трансляция логических выражений
Логические выражения, включающие логическое умножение, логическое сложение и отрицание, можно вычислять как непосредственно, используя таблицы истинности, так и с помощью условных выражений, основанных на следующих простых правилах:
A AND B эквивалентно if A then B else False,
A OR B эквивалентно if A then True else B.
Если в качестве компонент выражений могут входить функции с побочным эффектом, то, вообще говоря, результат вычисления может зависеть от способа вычисления. В некоторых языках программирования не оговаривается, каким способом должны вычисляться логические выражения (например, в Паскале), в некоторых требуется, чтобы вычисления производились тем или иным способом (например, в Модуле-2 требуется, чтобы выражения вычислялись по приведенным формулам), в некоторых языках есть возможность явно задать способ вычисления (Си, Ада). Вычисление логических выражений непосредственно по таблицам истинности аналогично вычислению арифметических выражений, поэтому мы не будем их рассматривать отдельно. Рассмотрим подробнее способ вычисления с помощью приведенных выше формул (будем называть его "вычислением с условными переходами"). Иногда такой способ рассматривают как оптимизацию вычисления логических выражений.
Рассмотрим следующую атрибутную грамматику со входным языком логических выражений:
RULE Expr ::= BoolExpr SEMANTICS FalseLab<1>=False; TrueLab<1>=True; Code<0>=Code<1>. RULE BoolExpr ::= BoolExpr 'AND' BoolExpr SEMANTICS FalseLab<1>=FalseLab<0>; TrueLab<1>=NodeLab<3>; FalseLab<3>=FalseLab<0>; TrueLab<3>=TrueLab<0>; Code<0>=NodeLab<0> + ":" + Code<1> + Code<3>. RULE BoolExpr ::= BoolExpr 'OR' BoolExpr SEMANTICS FalseLab<1>=NodeLab<3>; TrueLab<1>=TrueLab<0>; FalseLab<3>=FalseLab<0>; TrueLab<3>=TrueLab<0>; Code<0>=NodeLab<0> + ":" + Code<1> + Code<3>. RULE BoolExpr ::= F SEMANTICS Code<0>=NodeLab<0> + ":" + "GOTO" + FalseLab<0>. RULE BoolExpr ::= T SEMANTICS Code<0>=NodeLab<0> + ":" + "GOTO" + TrueLab<0>.
Здесь предполагается, что все вершины дерева занумерованы и номер вершины дает атрибут NodeLab. Метки вершин передаются, как это изображено на рис. 9.11.
Таким образом, каждому атрибутированному дереву в этой атрибутной грамматике сопоставляется код, полученный в результате обхода дерева сверху-вниз слева-направо
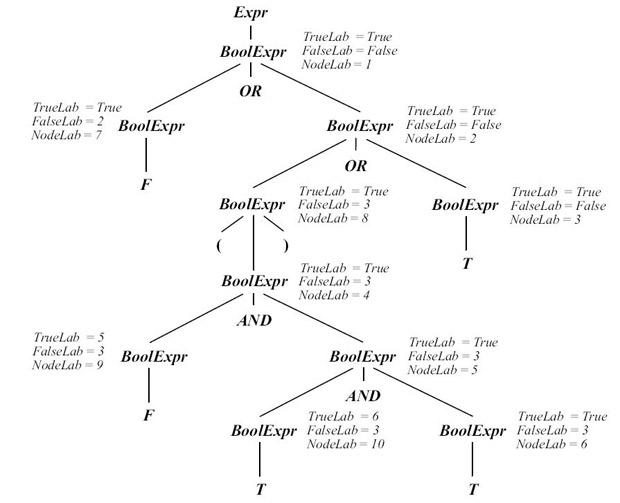
следующим образом. При входе в вершину BoolExpr генерируется ее номер, в вершине F генерируется текст GOTO значение атрибута FalseLab<0>, в вершине T - GOTO значение атрибута TrueLab<0>. Например, для выражения
F OR ( F AND T AND T ) OR T
получим атрибутированное дерево, изображенное на рис. 9.12, и код
1:7: GOTO 2 2:8:4:9: GOTO 3 5:10: GOTO 6 6: GOTO True 3: GOTO True True: ... False: ...
Эту линеаризованную запись можно трактовать как программу вычисления логического значения: каждая строка может быть помечена номером вершины и содержать либо переход на другую строку, либо переход на True или False, что соответствует значению выражения true или false. Будем говорить, что полученная программа вычисляет (или интерпретирует ) значение выражения, если в результате ее выполнения (от первой строки) мы придем к строке, содержащей GOTO True или GOTO False.
Утверждение 9.1. В результате интерпретации поддерева с некоторыми значениями атрибутов FalseLab и TrueLab в его корне выполняется команда GOTO TrueLab, если значение выражения истинно, и команда GOTO FalseLab, если значение выражения ложно.
Доказательство. Применим индукцию по высоте дерева. Для деревьев высоты 1, соответствующих правилам
BoolExpr ::= F и BoolExpr ::= T,
справедливость утверждения следует из соответствующих атрибутных правил. Пусть дерево имеет высоту n > 1. Зависимость атрибутов для дизъюнкции и конъюнкции приведена на рис. 9.13.
Если для конъюнкции значение левого поддерева ложно и по индукции вычисление левого поддерева
завершается командой GOTO FalseLab<1>, то получаем, что вычисление всего дерева завершается командой перехода GOTO FalseLab<0> (= FalseLab<1>). Если же значение левого поддерева истинно, то его вычисление завершается командой перехода GOTO TrueLab<1> (= NodeLab<3>). Если значение правого поддерева ложно, то вычисление всего дерева завершается командой GOTO FalseLab<0> (= FalseLab<3>). Если же оно истинно, вычисление всего дерева завершается командой перехода GOTO TrueLab<0> (= TrueLab<3>). Аналогично - для дизъюнкции.
Утверждение 9.2. Для любого логического выражения, состоящего из констант, программа, полученная в результате обхода дерева этого выражения, завершается со значением логического выражения в обычной интерпретации, то есть осуществляется переход на True для значения, равного true , и переход на метку False для значения false.
Доказательство. Это утверждение является частным случаем предыдущего. Его справедливость следует из того, что метки корня дерева равны соответственно TrueLab = True и FalseLab = False.
Добавим теперь новое правило в предыдущую грамматику:
RULE
BoolExpr ::= Ident
SEMANTICS
Code<0>=NodeLab<0> + ":" + "if (" + Val<1> +
"==T) GOTO" + TrueLab<0> + "else GOTO" +
FalseLab<0>.Тогда, например, для выражения A OR (B AND C AND D) OR E получим следующую программу:
1:7: if (A==T) GOTO True else GOTO 2 2:8:4:9: if (B==T) GOTO 5 else GOTO 3 5:10: if (C==T) GOTO 6 else GOTO 3 6: if (D==T) GOTO True else GOTO 3 3: if (E==T) GOTO True else GOTO False True: ... False: ...
При каждом конкретном наборе данных эта программа превращается в программу вычисления логического значения.
Утверждение 9.3. В каждой строке программы, сформированной предыдущей атрибутной схемой, одна из меток внутри условного оператора совпадает с меткой следующей строки.
Доказательство. Действительно, по правилам наследования атрибутов TrueLab и FalseLab, в правилах для дизъюнкции и конъюнкции либо атрибут FalseLab, либо атрибут TrueLab принимает значение метки следующего поддерева. Кроме того, как значение FalseLab, так и значение TrueLab, передаются в правое поддерево от предка. Таким образом, самый правый потомок всегда имеет одну из меток TrueLab или FalseLab, равную метке правого брата соответствующего поддерева. Учитывая порядок генерации команд, получаем справедливость утверждения.
Дополним теперь атрибутную грамматику следующим образом:
RULE
Expr ::= BoolExpr
SEMANTICS
FalseLab<1>=False; TrueLab<1>=True;
Sign<1>=false;
Code<0>=Code<1>.
RULE
BoolExpr ::= BoolExpr 'AND' BoolExpr
SEMANTICS
FalseLab<1>=FalseLab<0>; TrueLab<1>=NodeLab<3>;
FalseLab<3>=FalseLab<0>; TrueLab<3>=TrueLab<0>;
Sign<1>=false; Sign<3>=Sign<0>;
Code<0>=NodeLab<0> + ":" + Code<1> + Code<3>.
RULE
BoolExpr ::= BoolExpr 'OR' BoolExpr
SEMANTICS
FalseLab<1>=NodeLab<3>; TrueLab<1>=TrueLab<0>;
FalseLab<3>=FalseLab<0>; TrueLab<3>=TrueLab<0>;
Sign<1>=true; Sign<3>=Sign<0>;
Code<0>=NodeLab<0> + ":" + Code<1> + Code<3>.
RULE
BoolExpr ::= 'NOT' BoolExpr
SEMANTICS
FalseLab<2>=TrueLab<0>; TrueLab<2>=FalseLab<0>;
Sign<2>=! Sign<0>;
Code<0>=Code<2>.
RULE
BoolExpr ::= F
SEMANTICS
Code<0>=NodeLab<0> + ":" + "GOTO" + FalseLab<0>.
RULE
BoolExpr ::= T
SEMANTICS
Code<0>=NodeLab<0> + ":" + "GOTO" + TrueLab<0>.
RULE
BoolExpr ::= Ident
SEMANTICS
Code<0>=NodeLab<0> + ":" + "if (" + Val<1> +
"==T) GOTO" + TrueLab<0> + "else GOTO" +
FalseLab<0>.
Листинг
9.3.
Правила наследования атрибута Sign приведены на рис. 9.14.
Программу желательно сформировать таким образом, чтобы else -метка была как раз меткой следующей вершины. Как это можно сделать, следует из следующего утверждения.
Утверждение 9.4. В каждой терминальной вершине, метка ближайшего правого для нее поддерева равна значению атрибута FalseLab этой вершины, тогда и только тогда, когда значение атрибута Sign этой вершины равно true , и наоборот, метка ближайшего правого для нее поддерева равна значению атрибута TrueLab этой вершины, тогда и только тогда, когда значение атрибута Sign равно false.
Доказательство. Действительно, если ближайшей общей вершиной является AND, то в левого потомка передается Node - Lab правого потомка в качестве TrueLab и одновременно Sign правого потомка равен true. Если же ближайшей общей вершиной является OR, то в левого потомка передается NodeLab правого потомка в качестве FalseLab и одновременно Sign правого потомка равен false. Во все же правые потомки значения TrueLab, FalseLab и Sign передаются из предка (за исключением правила для NOT, в котором TrueLab и FalseLab меняются местами, но одновременно на противоположный меняется и Sign ).
Эти два утверждения (3 и 4) позволяют заменить последнее правило атрибутной грамматики следующим образом:
RULE
BoolExpr ::= Ident
SEMANTICS
Code<0>=NodeLab<0> + ":" +
(Sign<0>
? "if (" + Val<1> + "==T) GOTO" + TrueLab<0>
: "if (" + Val<1> + "==F) GOTO" + FalseLab<0>).В свою очередь, при генерации машинных команд это правило можно заменить на следующее:
RULE BoolExpr ::= Ident SEMANTICS Code<0>=NodeLab<0> + ":" + "TST" + Val<1> + (Sign<0> ? "BNE" + TrueLab<0> : "BEQ" + FalseLab<0>).
Таким образом, для выражения A OR (B AND C AND D) OR E получим следующий код на командах перехода:
1:7: TST A BNE True 2:8:4:9: TST B BEQ 3 5:10: TST C BEQ 3 6: TST D BNE True 3: TST E BEQ False True: ... False: ...
Если элементом логического выражения является сравнение, то генерируется команда, соответствующая знаку сравнения ( BEQ для =, BNE для <>, BGE для >= и т.д.), если атрибут Sign соответствующей вершины имеет значение true, и отрицание ( BNE для =, BEQ для <>, BLT для >= и т.д.), если атрибут Sign имеет значение false.