Лекция 6: Элементы теории перевода
До сих пор мы рассматривали процесс синтаксического анализа только как процесс анализа допустимости входной цепочки. Однако, в компиляторе синтаксический анализ служит основой еще одного важного шага - построения дерева синтаксического анализа. В примерах 4.3 и 4.8 предыдущей главы в процессе синтаксического анализа в качестве выхода выдавалась последовательность примененных правил, на основе которой и может быть построено дерево. Построение дерева синтаксического анализа является простейшим частным случаем перевода - процесса преобразования некоторой входной цепочки в некоторую выходную.
Определение. Пусть T - входной алфавит, а  - выходной алфавит. Переводом (или трансляцией) с языка
- выходной алфавит. Переводом (или трансляцией) с языка 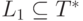 на язык
на язык 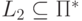 называется отображение
называется отображение  . Если
. Если  , то цепочка y называется выходом
для цепочки x.
, то цепочка y называется выходом
для цепочки x.
Мы рассмотрим несколько формализмов для определения переводов: преобразователи с магазинной памятью, схемы синтаксически управляемого перевода и атрибутные грамматики
Преобразователи с магазинной памятью
Рассмотрим важный класс абстрактных устройств, называемых преобразователями с магазинной памятью. Эти преобразователи получаются из автоматов с магазинной памятью, если к ним добавить выход и позволить на каждом шаге выдавать выходную цепочку.
Преобразователем с магазинной памятью (МП-преоб-
разователем) называется восьмерка 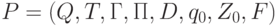 , где все символы имеют тот же смысл, что и в
определении МП-автомата, за исключением того, что
, где все символы имеют тот же смысл, что и в
определении МП-автомата, за исключением того, что  -
конечный выходной алфавит, а D - отображение множества
-
конечный выходной алфавит, а D - отображение множества 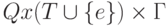 в множество конечных подмножеств
множества
в множество конечных подмножеств
множества 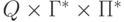 .
.
Определим конфигурацию преобразователя P как
четверку (q, x, u, y), где 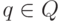 - состояние,
- состояние, 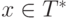 - цепочка на входной ленте,
- цепочка на входной ленте, 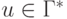 - содержимое магазина,
- содержимое магазина,  - цепочка на выходной ленте, выданная вплоть до настоящего момента.
- цепочка на выходной ленте, выданная вплоть до настоящего момента.
Если множество D(q, a, Z) содержит элемент (r, u, z), то
будем писать 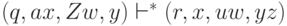 для любых
для любых 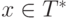 ,
, 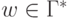 и
и  : Рефлексивно - транзитивное замыкание
отношения
: Рефлексивно - транзитивное замыкание
отношения 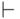 будем обозначать
будем обозначать 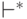 .
.
Цепочку y назовем выходом для x, если 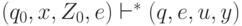 для некоторых
для некоторых 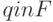 и
и 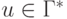 . Переводом
(или трансляцией), определяемым МП-преобразователем P
(обозначается
. Переводом
(или трансляцией), определяемым МП-преобразователем P
(обозначается 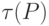 ), назовем множество
), назовем множество
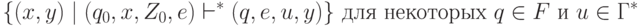
Будем говорить, что МП-преобразователь P является детерминированным (ДМП-преобразователем), если выполняются следующие условия:
- для всех
 и
и 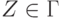 множество D(q, a, Z)
содержит не более одного элемента,
множество D(q, a, Z)
содержит не более одного элемента, - если
 , то
, то 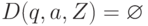 для всех
для всех  .
.
Пример 5.1. Рассмотрим перевод 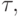 отображающий каждую
цепочку
отображающий каждую
цепочку 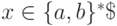 , в которой число вхождений символа a равно числу вхождений символа b, в цепочку y = (ab)n, где n - число вхождений a или b в цепочку x. Например,
, в которой число вхождений символа a равно числу вхождений символа b, в цепочку y = (ab)n, где n - число вхождений a или b в цепочку x. Например,  .
.
Этот перевод может быть реализован ДМП-преобразователем P = ({q0, qf}, {a, b, $}, {Z, a, b}, {a, b}, D, q0, Z, {qf}) c функцией переходов:
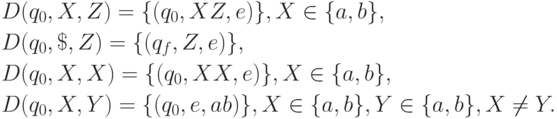
Синтаксически управляемый перевод
Другим формализмом, используемым для определения переводов, является схема синтаксически управляемого перевода. Фактически, такая схема представляет собой КС- грамматику, в которой к каждому правилу добавлен элемент перевода. Всякий раз, когда правило участвует в выводе входной цепочки, с помощью элемента перевода вычисляется часть выходной цепочки, соответствующая части входной цепочки, порожденной этим правилом.
Схемы синтаксически управляемого перевода
Определение. Cхемой синтаксически управляемого
перевода (или трансляции, сокращенно: СУ-схемой)
называется пятерка 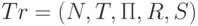 , где
, где
(1) N - конечное множество нетерминальных символов;
(2) T - конечный входной алфавит;
 - конечный выходной алфавит;
- конечный выходной алфавит;
R - конечное множество правил перевода вида
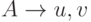
где 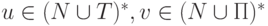 и вхождения
нетерминалов в цепочку v образуют перестановку
вхождений нетерминалов в цепочку u, так что каждому
вхождению нетерминала B в цепочку u соответствует
некоторое вхождение этого же нетерминала в цепочку v ; если нетерминал B встречается более одного
раза, для указания соответствия используются верхние
целочисленные индексы;
и вхождения
нетерминалов в цепочку v образуют перестановку
вхождений нетерминалов в цепочку u, так что каждому
вхождению нетерминала B в цепочку u соответствует
некоторое вхождение этого же нетерминала в цепочку v ; если нетерминал B встречается более одного
раза, для указания соответствия используются верхние
целочисленные индексы;
(5) S - начальный символ, выделенный нетерминал из N.
Определим выводимую пару в схеме Tr следующим образом:
(1) (S, S) - выводимая пара, в которой символы S соответствуют друг другу;
(2) если (xAy; x'Ay') - выводимая пара, в цепочках
которой вхождения A соответствуют друг другу, и A -> u, v - правило из R, то (xuy; x'vy') -
выводимая пара. Для обозначения такого вывода одной
пары из другой будем пользоваться обозначением 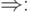 (xAy, x'Ay') => (xuy, x'vy'). Рефлексивно-транзитивное
замыкание отношение
(xAy, x'Ay') => (xuy, x'vy'). Рефлексивно-транзитивное
замыкание отношение  обозначим =>*.
обозначим =>*.
Переводом 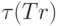 , определяемым СУ-схемой Tr, назовем
множество пар
, определяемым СУ-схемой Tr, назовем
множество пар
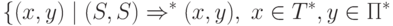
Если через P обозначить множество входных правил вывода всех правил перевода, то G = (N, T, P, S) будет входной грамматикой для Tr.
СУ-схема 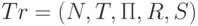 называется простой, если
для каждого правила A -> u, v из R соответствующие друг
другу вхождения нетерминалов встречаются в u и v в одном
и том же порядке.
называется простой, если
для каждого правила A -> u, v из R соответствующие друг
другу вхождения нетерминалов встречаются в u и v в одном
и том же порядке.
Перевод, определяемый простой СУ-схемой, называется простым синтаксически управляемым переводом (простым СУ-переводом).
Пример 5.2. Перевод арифметических выражений в ПОЛИЗ (польскую инверсную запись) можно осуществить простой СУ-схемой с правилами
Найдем выход схемы для входа id * (id + id). Нетрудно видеть, что существует последовательность шагов вывода
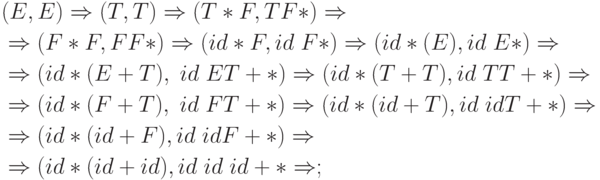
переводящая эту цепочку в цепочку id id id + *.
Рассмотрим связь между переводами, определяемыми СУ- схемами и осуществляемыми МП-преобразователями [2].
