Генерация кода
Выделение общих подвыражений
Выделение общих подвыражений относится к области оптимизации программ. В общем случае трудно (или даже невозможно) провести границу между оптимизацией и "качественной трансляцией". Оптимизация - это и есть качественная трансляция. Обычно термин "оптимизация" употребляют, когда для повышения качества программы используют ее глубокие преобразования такие, например, как перевод в графовую форму для изучения нетривиальных свойств программы.
В этом смысле выделение общих подвыражений - одна из простейших оптимизаций. Для ее осуществления требуется некоторое преобразование программы, а именно построение ориентированного ациклического графа, о котором говорилось в главе, посвященной промежуточным представлениям.
Линейный участок - это последовательность операторов, в которую управление входит в начале и выходит в конце без остановки и перехода изнутри.
Рассмотрим дерево линейного участка, в котором вершинами служат операции, а потомками - операнды. Будем говорить, что две вершины образуют общее подвыражение, если поддеревья для них совпадают, то есть имеют одинаковую структуру и, соответственно, одинаковые операции во внутренних вершинах и одинаковые операнды в листьях. Выделение общих подвыражений позволяет генерировать для них код один раз, хотя может привести и к некоторым трудностям, о чем вкратце будет сказано ниже.
Выделение общих подвыражений проводится на линейном участке и основывается на двух положениях.Выделение общих подвыражений проводится на линейном участке и основывается на двух положениях.
- Поскольку на линейном участке переменной может быть несколько присваиваний, то при выделении общих подвыражений необходимо различать вхождения переменных до и после присваивания. Для этого каждая переменная снабжается счетчиком. Вначале счетчики всех переменных устанавливаются равными 0. При каждом присваивании переменной ее счетчик увеличивается на 1.
- Выделение общих подвыражений осуществляется при обходе дерева выражения снизу вверх слева направо. При достижении очередной вершины (пусть операция, примененная в этой вершине, есть бинарная op ; в случае унарной операции рассуждения те же) просматриваем общие подвыражения, связанные с op. Если имеется выражение, связанное с op и такое, что его левый операнд есть общее подвыражение с левым операндом нового выражения, а правый операнд - общее подвыражение с правым операндом нового выражения, то объявляем новое выражение общим с найденным и в новом выражении запоминаем указатель на найденное общее выражение. Базисом построения служит переменная: если операндами обоих выражений являются одинаковые переменные с одинаковыми счетчиками, то они являются общими подвыражениями. Если выражение не выделено как общее, оно заносится в список операций, связанных с op.
Рассмотрим теперь реализацию алгоритма выделения общих подвыражений. Поддерживаются следующие глобальные переменные:
Table - таблица переменных; для каждой переменной хранится ее счетчик ( Count ) и указатель на вершину дерева выражений, в которой переменная встретилась в последний раз в правой части ( Last );
OpTable - таблица списков (типа LisType ) общих подвыражений, связанных с каждой операцией. Каждый элемент списка хранит указатель на вершину дерева (поле Addr ) и продолжение списка (поле List ).
С каждой вершиной дерева выражения связана запись типа NodeType, со следующими полями:
Left - левый потомок вершины,
Right - правый потомок вершины,
Comm - указатель на предыдущее общее подвыражение,
Flag - признак, является ли поддерево общим подвыражением,
Varbl - признак, является ли вершина переменной,
VarCount - счетчик переменной. Выделение общих подвыражений и построение дерева осуществляются приведенными ниже правилами. Атрибут Entry нетерминала Variable дает указатель на переменную в таблице Table. Атрибут Val символа Op дает код операции. Атрибут Node символов IntExpr и Assignment дает указатель на запись типа NodeType соответствующего нетерминала.
RULE
Assignment ::= Variable IntExpr
SEMANTICS
Table[Entry<1>].Count=Table[Entry<1>].Count+1.
// Увеличить счетчик присваиваний переменной
RULE
IntExpr ::= Variable
SEMANTICS
if ((Table[Entry<1>].Last!=NULL)
// Переменная уже была использована
&& (Table[Entry<1>].Last->VarCount
== Table[Entry<1>].Count ))
// С тех пор переменной не было присваивания
{Node<0>->Flag=true;
// Переменная - общее подвыражение
Node<0>->Comm= Table[Entry<1>].Last;
// Указатель на общее подвыражение
}
else Node<0>->Flag=false;
Table[Entry<1>].Last=Node<0>;
// Указатель на последнее использование переменной
Node<0>->VarCount= Table[Entry<1>].Count;
// Номер использования переменной
Node<0>->Varbl=true.
// Выражение - переменная
RULE
IntExpr ::= Op IntExpr IntExpr
SEMANTICS
LisType * L; //Тип списков операции
if ((Node<2>->Flag) && (Node<3>->Flag))
// И справа, и слева - общие подвыражения
{L=OpTable[Val<1>];
// Начало списка общих подвыражений для операции
while (L!=NULL)
if ((Node<2>==L->Left)
&& (Node<3>==L->Right))
// Левое и правое поддеревья совпадают
break;
else L=L->List;// Следующий элемент списка
}
else L=NULL; //Не общее подвыражение
Node<0>->Varbl=false; // Не переменная
Node<0>->Comm=L;
// Указатель на предыдущее общее подвыражение
// или NULL
if (L!=NULL)
{Node<0>->Flag=true; //Общее подвыражение
Node<0>->Left=Node<2>;
// Указатель на левое поддерево
Node<0>->Right=Node<3>;
// Указатель на правое поддерево
}
else {Node<0>->Flag=false;
// Данное выражение не может рассматриваться
// как общее. Если общего подвыражения с
// данным не было, включить данное в список
// для операции
L=alloc(sizeof(struct LisType));
L->Addr=Node<0>;
L->List=OpTable[Val<1>];
OpTable[Val<1>]=L;
}.
Листинг
9.4.
Рассмотрим теперь некоторые простые правила распределения регистров при наличии общих подвыражений. Если число регистров ограничено, можно выбрать один из следующих двух вариантов.
- При обнаружении общего подвыражения с подвыражением в уже просмотренной части дерева (и, значит, с уже распределенными регистрами) проверяем, расположено ли его значение на регистре. Если да, и если регистр после этого не менялся, заменяем вычисление поддерева на значение в регистре. Если регистр менялся, то вычисляем подвыражение заново.
- Вводим еще один проход. На первом проходе распределяем регистры. Если в некоторой вершине обнаруживается, что ее поддерево общее с уже вычисленным ранее, но значение регистра потеряно, то в такой вершине на втором проходе необходимо сгенерировать команду сброса регистра в рабочую память. Выигрыш в коде будет, если стоимость команды сброса регистра + доступ к памяти в повторном использовании этой памяти не превосходит стоимости заменяемого поддерева. Поскольку стоимость команды MOVE известна, можно сравнить стоимости и принять оптимальное решение: пометить предыдущую вершину для сброса либо вычислять поддерево полностью.
Трансляция объектно-ориен- тированных свойств языков программирования
В этом разделе будут рассмотрены механизмы трансляции базовых конструкций объектно-ориентированных языков программирования, а именно наследования и виртуальных функций на примере языка С++.
Виртуальные базовые классы
К описателю базового класса можно добавить ключевое слово virtual. В этом случае единственный подобъект виртуального базового класса разделяется каждым базовым классом, в котором тот, исходный, базовый класс определен как виртуальный.
Пусть мы имеем следующую иерархию наследования:
class L {. . . }
class A : public virtual L {. . . }
class B : public virtual L {. . . }
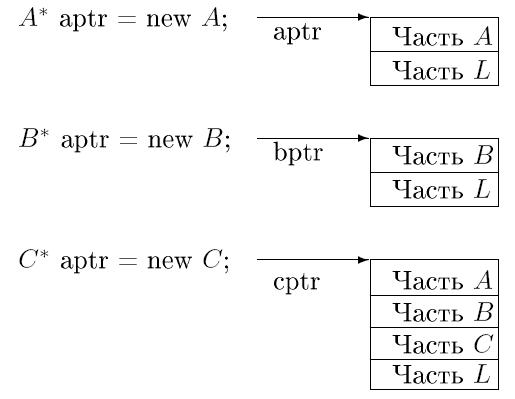
class C : public A, public B {. . . }Это можно изобразить следующей диаграммой классов:
Каждый объект A или объект B будет содержать L, но в объекте C будет существовать лишь один объект класса L. Ясно, что представление объекта виртуального базового класса L не может быть в одной и той же позиции относительно и A, и B для всех объектов. Следовательно, во всех объектах классов, которые включают класс L как виртуальный базовый класс, должен храниться указатель на L. Реализация A, B и C объектов могла бы выглядеть следующим образом:
Множественное наследование
Имея два класса
class A {. . . af (int);}
class B {. . . bf (int); }можно объявить третий класс с этими двумя в качестве базовых:
class C : public A, public B {. . . }Объект класса C может быть размещен как непрерывный объект вида:
Как и в случае с единичным наследованием, здесь не гарантируется порядок выделения памяти для базовых классов, поэтому объект класса C может выглядеть и так:
Доступ к члену класса A, B или C реализуется в точности так же, как и для единичного наследования: компилятор знает положение в объекте каждого члена и порождает соответствующий код.
Если объект размещен в памяти в соответствии с первой диаграммой: сначала часть A объекта, а затем части B и C, то вызов функции - члена класса A или C будет таким же, как вызов функции-члена при единичном наследовании. Вызов функции-члена класса B для объекта, заданного указателем на C, реализуется несколько сложнее. Рассмотрим
C* pc = new C; pc -> bf(2);
Функция B :: bf() естественно предполагает, что ее параметр this является указателем на B. Чтобы получить указатель на часть B объекта C, следует добавить к указателю pc смещение B относительно C - константу времени компиляции, которую мы будем называть delta(B). Соотношение указателя pc и указателя this, передаваемого в B::bf, показано ниже.