|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Классические шифры
6.4 Шифры замены
Шифр замены является простейшим, наиболее популярным шифром. Типичными примерами являются шифр Цезаря, "цифирная азбука" Петра Великого и "пляшущие человечки" А. Конан Дойла. Как видно из самого названия, шифр замены осуществляет преобразование замены букв или других "частей" открытого текста на аналогичные "части" шифрованного текста. Дадим математическое описание шифра замены. Пусть  и
и  - два алфавита (открытого и шифрованного текстов соответственно), состоящие из одинакового числа символов. Пусть также
- два алфавита (открытого и шифрованного текстов соответственно), состоящие из одинакового числа символов. Пусть также 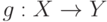 - взаимнооднозначное отображение
- взаимнооднозначное отображение  в
в  . Тогда шифр замены действует так: открытый текст
. Тогда шифр замены действует так: открытый текст  преобразуется в шифрованный текст
преобразуется в шифрованный текст 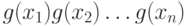 .
.
6.4.1 Математическая модель шифра замены
([1])
Определим модель  произвольного шифра замены. Будем считать, что открытые и шифрованные тексты являются словами в алфавитах
произвольного шифра замены. Будем считать, что открытые и шифрованные тексты являются словами в алфавитах  и
и  соответственно:
соответственно: 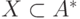 ,
,  ,
,  ,
,  . Здесь и далее
. Здесь и далее 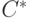 обозначает множество слов конечной длины в алфавите
обозначает множество слов конечной длины в алфавите  .
.
Перед зашифрованием открытый текст предварительно представляется в виде последовательности подслов, называемых шифрвеличинами. При зашифровании шифрвеличины заменяются некоторыми их эквивалентами в шифртексте, которые назовем шифробозначениями. Как шифрвеличины, так и шифробозначения представляют собой слова из 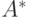 и
и 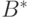 соответственно.
соответственно.
Пусть  - множество возможных шифрвеличин,
- множество возможных шифрвеличин,  - множество возможных шифробозначений. Эти множества должны быть такими, чтобы любые тексты
- множество возможных шифробозначений. Эти множества должны быть такими, чтобы любые тексты  ,
,  можно было представить словами из
можно было представить словами из 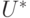 ,
,  соответственно. Требование однозначности расшифрования влечет неравенства
соответственно. Требование однозначности расшифрования влечет неравенства 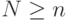 ,
,  ,
,  .
.
6.4.2 Криптоанализ шифра простой замены
Криптоанализ шифра простой замены основан на использовании статистических закономерностей языка. Приведем таблицы частот букв русского и английского языков, следуя [1].
 |
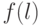 |
 |
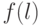 |
 |
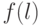 |
 |
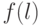 |
|---|---|---|---|---|---|---|---|
| - | 0,175 | О | 0,09 | Е, Ё | 0,72 | А | 0,062 |
| И | 0,062 | Т | 0,053 | Н | 0,053 | С | 0,045 |
| Р | 0,040 | В | 0,038 | Л | 0,035 | К | 0,028 |
| М | 0,026 | Д | 0,025 | П | 0,023 | У | 0,021 |
| Я | 0,018 | Ы | 0,016 | 3 | 0,016 | Ь,Ъ | 0,014 |
| Б | 0,014 | Г | 0,013 | Ч | 0,012 | Й | 0,010 |
| X | 0,009 | Ж | 0,007 | Ю | 0,006 | Ш | 0,006 |
| Ц | 0,004 | Щ | 0,003 | Э | 0,003 | Ф | 0,002 |
Полезной является диаграмма рис. 6.2
Для получения более точных сведений об открытых текстах можно строить и анализировать таблицы  -грамм при
-грамм при  , однако для учебных целей вполне достаточно ограничиться биграммами. Неравновероятность
, однако для учебных целей вполне достаточно ограничиться биграммами. Неравновероятность  -грамм (и даже слов) тесно связана с характерной особенностью открытого текста - наличием в нем большого числа повторений отдельных фрагментов текста: корней, окончаний, суффиксов, слов и фраз. Так, для русского языка такими привычными фрагментами являются наиболее частые биграммы и триграммы:
-грамм (и даже слов) тесно связана с характерной особенностью открытого текста - наличием в нем большого числа повторений отдельных фрагментов текста: корней, окончаний, суффиксов, слов и фраз. Так, для русского языка такими привычными фрагментами являются наиболее частые биграммы и триграммы:
СТ, НО, ЕН, ТО, НА, ОВ, НИ, РА, ВО, КО,
СТО, ЕНО, НОВ, ТОВ, ОВО, ОВА
Полезной является информация о сочетаемости букв, т. е. о предпочтительных связях букв друг с другом, которую легко извлечь из таблиц частот биграмм.
Имеется в виду таблица, в которой слева и справа от каждой буквы расположены наиболее предпочтительные "соседи" (в порядке убывания частоты соответствующих биграмм). В таких таблицах обычно указывается также доля гласных и согласных букв (в процентах), предшествующих (или следующих за) данной букве.
| А | Б | В | Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| А | 2 | 12 | 35 | 8 | 14 | 7 | 6 | 15 | 7 | 7 | 19 | 27 | 19 | 45 | 3 | 11 |
| Б | 5 | 9 | 1 | 6 | 6 | 2 | 21 | |||||||||
| В | 35 | 1 | 5 | 3 | 3 | 32 | 2 | 17 | 7 | 10 | 3 | 9 | 58 | 6 | ||
| Г | 7 | 3 | 3 | 5 | 1 | 5 | 1 | 50 | ||||||||
| Д | 25 | 3 | 1 | 1 | 29 | 1 | 1 | 13 | 1 | 5 | 1 | 13 | 22 | 3 | ||
| Е | 2 | 9 | 18 | 11 | 27 | 7 | 5 | 10 | 6 | 15 | 13 | 35 | 24 | 63 | 7 | 16 |
| Ж | 5 | 1 | 6 | 12 | 5 | 6 | ||||||||||
| 3 | 35 | 1 | 7 | 1 | 5 | 3 | 4 | 2 | 1 | 2 | 9 | 9 | 1 | |||
| И | 4 | 6 | 22 | 5 | 10 | 21 | 2 | 23 | 19 | 11 | 19 | 21 | 20 | 32 | 8 | 13 |
| И | 1 | 1 | 4 | 1 | 3 | 1 | 2 | 4 | 5 | 1 | 2 | 7 | 9 | 7 | ||
| К | 24 | 1 | 4 | 1 | 4 | 1 | 1 | 26 | 1 | 4 | 1 | 2 | 66 | 2 | ||
| Л | 25 | 1 | 1 | 1 | 1 | 33 | 2 | 1 | 36 | 1 | 2 | 1 | 8 | 30 | 2 | |
| М | 18 | 2 | 4 | 1 | 1 | 21 | 1 | 2 | 23 | 3 | 1 | 3 | 7 | 19 | 5 | |
| Н | 54 | 1 | 2 | 3 | 3 | 34 | 58 | 3 | 1 | 24 | 67 | 2 | ||||
| О | 1 | 28 | 84 | 32 | 47 | 15 | 7 | 18 | 12 | 29 | 19 | 41 | 38 | 30 | 9 | 18 |
| П | 7 | 15 | 4 | 9 | 1 | 46 | ||||||||||
| Р | 55 | 1 | 4 | 4 | 3 | 37 | 3 | 1 | 24 | 3 | 1 | 3 | 7 | 56 | 2 | |
| С | 8 | 1 | 7 | 1 | 2 | 25 | 6 | 40 | 13 | 3 | 9 | 27 | 11 | |||
| Т | 35 | 1 | 27 | 1 | 3 | 31 | 1 | 28 | 5 | 1 | 1 | 11 | 56 | 4 | ||
| У | 1 | 4 | 4 | 4 | 11 | 2 | 6 | 3 | 2 | 8 | 5 | 5 | 5 | 1 | 5 | |
| Ф | 2 | 2 | 2 | 1 | ||||||||||||
| X | 4 | 1 | 4 | 1 | 3 | 1 | 2 | 3 | 4 | 3 | 3 | 4 | 18 | 5 | ||
| Ц | 3 | 7 | 10 | 2 | 1 | |||||||||||
| Ч | 12 | 23 | 13 | 2 | 6 | |||||||||||
| Ш | 5 | 11 | 14 | 1 | 2 | 2 | 2 | |||||||||
| Щ | 3 | 8 | 6 | 1 | ||||||||||||
| Ы | 1 | 9 | 1 | 3 | 12 | 2 | 4 | 7 | 3 | 6 | 6 | 3 | 2 | 10 | ||
| Ь | 2 | 4 | 1 | 1 | 2 | 2 | 2 | 6 | 3 | 13 | 2 | 4 | ||||
| Э | 1 | 1 | ||||||||||||||
| Ю | 2 | 1 | 2 | 1 | 3 | 1 | 1 | 1 | 1 | 1 | 3 | |||||
| Я | 1 | 3 | 9 | 1 | 3 | 3 | 1 | 5 | 3 | 2 | 3 | 3 | 4 | 6 | 3 | 6 |
| Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ы | Ь | Э | Ю | Я | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| А | 26 | 31 | 27 | 3 | 1 | 10 | 6 | 7 | 10 | 1 | 2 | 6 | 9 | ||
| Б | 8 | 1 | 6 | 1 | 11 | 2 | |||||||||
| В | 6 | 19 | 6 | 7 | 1 | 1 | 2 | 4 | 1 | 18 | 1 | 2 | 3 | ||
| Г | 7 | 2 | |||||||||||||
| Д | 6 | 8 | 1 | 10 | 1 | 1 | 1 | 5 | 1 | 1 | |||||
| Е | 39 | 37 | 33 | 3 | 1 | 8 | 3 | 7 | 3 | 3 | 1 | 1 | 2 | ||
| Ж | 1 | ||||||||||||||
| 3 | 3 | 1 | 2 | 4 | 4 | ||||||||||
| И | 11 | 29 | 29 | 3 | 1 | 17 | 3 | 11 | 1 | 1 | 1 | 3 | 17 | ||
| И | 3 | 10 | 2 | 1 | 3 | 2 | |||||||||
| К | 10 | 3 | 7 | 10 | 1 | ||||||||||
| Л | 3 | 1 | 6 | 4 | 1 | 2 | 30 | 4 | 9 | ||||||
| М | 2 | 5 | 3 | 9 | 1 | 2 | 5 | 1 | 1 | 3 | |||||
| Н | 1 | 9 | 9 | 7 | 1 | 5 | 2 | 36 | 3 | 5 | |||||
| О | 43 | 50 | 39 | 3 | 2 | 5 | 2 | 12 | 4 | 3 | 2 | 3 | 2 | ||
| П | 41 | 1 | 6 | 2 | 2 | ||||||||||
| Р | 1 | 5 | 9 | 16 | 1 | 1 | 1 | 2 | 8 | 3 | 5 | ||||
| С | 4 | 11 | 82 | 6 | 1 | 1 | 2 | 2 | 1 | 8 | 17 | ||||
| Т | 26 | 18 | 2 | 10 | 1 | И | 21 | 4 | |||||||
| У | 7 | 14 | 7 | 1 | 8 | 3 | 2 | 9 | 1 | ||||||
| Ф | 1 | 1 | |||||||||||||
| X | 3 | 4 | 2 | 2 | 1 | 1 | |||||||||
| Ц | 1 | 1 | |||||||||||||
| Ч | 7 | 1 | 1 | 1 | |||||||||||
| Ш | 1 | 1 | |||||||||||||
| Щ | 1 | ||||||||||||||
| Ы | 3 | 9 | 4 | 1 | 16 | 1 | 2 | ||||||||
| Ь | 1 | 11 | 3 | 1 | 4 | 1 | 3 | 1 | |||||||
| Э | 1 | 9 | |||||||||||||
| Ю | 1 | 1 | 7 | 1 | 1 | 4 | |||||||||
| Я | 3 | 6 | 10 | 2 | 1 | 4 | 1 | 1 | 1 | 1 | 1 |
Пример 6.5 [3] Известно, что зашифровано стихотворение Р. Киплинга в переводе С.Я. Маршака. Шифрование заключалось в замене каждой буквы на двузначное число. Отдельные слова разделены несколькими пробелами, знаки препинания сохранены. Таблица частот букв русского языка приведена выше.
29 15 10 17 29 22 25 31 15 33 35 41 43 45 35 57 45 25 17 59 15 10 25 41
25 69, 59 78 29 82 25 78 25 17 15 10 88 90 78 25 62 25 22 10 57 73 79 35 67
78 90 88 29 45 35 29, 54 57 90 31 90 73 22 88 15 88 29 15 17 69 41 25 15, 70
17 90 57 43 59 15 78 15 62 22 25 17 57 25 69 88 15 82 17 25 88 29 45 35. . .
Решение. Подсчитаем частоты шифробозначений:
| Обозначение | 29 | 15 | 10 | 17 | 22 | 25 | 31 | 33 | 35 | 41 | 43 | 45 | 57 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Количество | 7 | 10 | 4 | 7 | 4 | 12 | 2 | 1 | 5 | 3 | 2 | 4 | 5 |
| Обозначение | 59 | 69 | 78 | 82 | 88 | 90 | 62 | 73 | 79 | 67 | 54 | 70 | |
| Количество | 3 | 3 | 4 | 2 | 6 | 5 | 1 | 2 | 1 | 1 | 1 | 1 |
Из таблицы частот букв русского языка видно, что чаще всего встречается буква О, на втором месте Е. В нашем шифртексте чаще всего встречается обозначение 25 (12 раз), на втором месте идет обозначение 15 (10 раз), остальные обозначения им существенно уступают. Поэтому можем выдвинуть гипотезу: 25=О, 15=Е. Однако текст у нас не очень большой, поэтому закономерности русского языка проявляются в нем не обязательно в строгом соответствии с таблицей частот букв русского языка. Поэтому возможен и вариант: 25=Е, 15=О. Но тогда последнее слово в третьей строке имеет окончание ЕО, что возможно, но все же более вероятный вариант ОЕ. Итак, будем работать с текстом, считая, что 25=О, 15=Е.
Теперь нам поможет знак препинания: "29, {\dots}". Крайне маловероятно, чтобы запятая стояла после согласной. Итак, 29 - гласная, причем вероятнее всего 29=И или 29=А, т. к. гласные Я, Ю, Э, У встречаются в осмысленных текстах на русском языке намного реже, чем И и А, что не противоречит таблице частот шифртекста.
В последней строке: 88 15, но 15=Е, следовательно, 88 - согласная, причем наиболее вероятные значения - это Н и Т. Итак, 25=О, 15=Е,  ,
,  . Теперь третье слово в третьей строке имеет 4 варианта:
. Теперь третье слово в третьей строке имеет 4 варианта:
- 29=И, 88=Н: 22 Н Е Н И Е
- 29=И, 88=Т:22 Т Е Т И Е
- 29=А, 88=Н:22 Н Е Н А Е
- 29=А, 88=Т: 22 Т Е Т А Е
Из рассмотренных вариантов лишь один является осмысленным, и он позволяет найти значение 22. Имеем: 22=М и третье слово в третье строке - М Н Е Н И Е.
Теперь рассмотрим второе слово в первой строке. Е 10 17 И, причем 10 и 17 - согласные, и это не М и не Н. Наиболее вероятное слово Е С Л И, т. е. 10=С, 17=Л. Конечно, если мы, продолжая работать с текстом, вдруг получим "нечитаемое" слово, то придется вернуться к этому этапу и рассмотреть другие варианты. Однако это маловероятно, поскольку вряд ли в стихотворении были слова наподобие Е Р Т И, Е В Л И и т. п.
Далее, первое слово второй строки: 59 78 И, причем 59 и 78 - согласные, и это не С, не Л, не М и не Н. Так что это слово П Р И, т. е. 59=П, 78=Р. Тогда шестое слово первой строки 45 О Л П Е, что дает значение 45=Т, и тогда при 57=В получаем фрагмент "... В Т О Л П Е ...". Также второе слово последней строки П Е Р Е 62 дает нам значение 62=Д.
Далее рассмотрим начало второй строки: "П Р И 82 О Р О Л Е С Н 90 Р О Д О М ...". Из него следует, что 82=К и 90=А. Зная, что 82=К, посмотрим на самое последнее слово К Л О Н И Т 35, откуда станет ясно, что 35=Ь.
Перед последней атакой выпишем текст, заменяя известные обозначения буквами.
И Е С Л И М О 31 Е 33 Ь 41 43 Т Ь В Т О Л П Е С О 41 О 69,
П Р И К О Р О Л Е С Н А Р О Д О М С В 73 79 Ь 67 Р А Н И Т Ь
И, 54 В А 31 А 73 М Н Е Н И Е Л 69 41 О Е,
70 Л А В 43 П Е Р Е Д М О Л В О 69 Н Е К Л О Н И Т Ь ...
Из последней строки: 69=Ю, тогда слова Л Ю 41 О Е и С О 41 О Ю определяют 41: 41=Б. Теперь из четвертого слова первой строки Б 43 Т Ь получаем, что 43=Ы. А первое слово из последней строки 70 Л А В Ы - это Г Л А В Ы. Слово в первой строке М О 31 Е 33 Ь угадывается из контекста: М О Ж Е Ш Ь, т. е. 31=Ж, 33=Ш. Теперь второе слово в третьей строке запишется как 54 В А Ж А 73, откуда с учетом контекста: 54=У, 73=Я. После этого окончание второй строки имеет вид "... С В Я 79 Ь 67 Р А Н И Т Ь". Легко определяются буквы 79=З, 67=Х.
Ответ:
И Е С Л И М О Ж Е Ш Ь Б Ы Т Ь В Т О Л П Е С О Б О Ю,
П Р И К О Р О Л Е С Н А Р О Д О М С В Я З Ь Х Р А Н И Т Ь
И, У В А Ж А Я М Н Е Н И Е Л Ю Б О Е,
Г Л А В Ы П Е Р Е Д М О Л В О Ю Н Е К Л О Н И Т Ь...
Пример 6.6 То же самое задание:
56 67 92 18 58 39 99 27 87 67 56 25 56 80 67 10 17 92 39 62 25 56 27 24
95 56 31 95 46 27 73 56 31 17 58 39 58 67 95 58 92 56 95 40 24 40 17 92 39
62 69 39 40 17 56 67 58 - 56 18 99 92 46 67 56 87, 69 56 69 39 36 80 17 92
67 27 39 40 87 56 17 58 73 40. 25 56 39 73 56 10 17 92, 56 43 92 80 40 10, 95
56 23 80 40 23 17 40 24 40 25 46 92 69 14 95 67 27 73 95 73 58 87 67 56 73
58. 69 39 58 69 56 95 46 27 23 25 46 92 67 10 17 56 38 58 73 95 92 58 56 38
58 46 73 40 67 92 10. 25 46 92 18 56 46 56 69 92 25 27 17 62 73 56 69 24 80
58 39 62 18 14 17 56 25 46 58 69 58 17 92 95 56 58 87 67 56 43 58 39 73 69
56, 23 17 40 24 40 46 40 24 18 58 23 40 17 92 39 62. 56 80 67 40 95 56 18 17
40 23 56 80 40 46 10 73 58 87 43 58 80 69 27 87 67 58 80 58 17 10 87 73 46
58 67 92 46 56 69 56 95 67 40 87 40 95 58 73 58 92 73 14 39 10 38 58 95 46
40 73 67 56 25 56 69 73 56 46 58 67 67 14 87 67 40 39 73 40 69 17 58 67 92
10 87 92 67 39 73 46 27 95 73 56 46 40 56 67 92 39 56 69 58 46 99 58 67 67
156 73 56 38 67 56 24 67 40 17 92, 24 40 38 58 87 25 46 92 99 17 92. 25 56 67
10 73 92 10 67 58 92 87 58 17 92, 80 17 10 38 58 23 56 95 56 67 95 46 58 73
67 56 25 46 58 80 67 40 24 67 40 38 58 67 14 69 39 58 71 73 92 99 73 27 95
92 - 67 56 56 73 67 92 82 71 73 56 23 56 92 67 58 73 46 58 18 56 69 40 17 56
39 62.
67 58 25 46 56 99 17 56 92 87 92 67 27 73 14, 95 40 95 56 67 27 69 92 80
58 17 51 58 17 62 92 82 67 58 17 58 23 95 56 23 56 92 71 95 24 56 73 92 38
58 39 95 56 23 56 25 27 73 58 99 58 39 73 69 92 10 - 73 46 92 25 27 17 62 73
40 25 56 25 46 40 69 56 87 27 18 56 46 73 27, 27 39 14 25 40 67 67 14 58 38
58 46 73 56 69 56 31 27 31 87 56 31 73 27 87 18 17 58 46 56 69, 17 40 87 25
56 38 58 95, 25 58 46 58 95 17 36 38 40 73 58 17 58 31 92 95 67 56 25 56 95.
73 46 92 69 14 25 27 95 17 14 82 71 95 46 40 67 40 69 69 92 80 58 69 58 46
73 92 95 40 17 62 67 14 82 25 46 10 87 56 27 23 56 17 62 67 92 95 56 69 - 56
67 92 39 40 87 14 58, 67 92 95 40 95 56 31 56 99 92 18 95 92. . .
18 56 80 46 56 39 73 92 46 40 80 92, 56 67 25 56 69 73 56 46 92 17 25 46
56 39 58 18 10 25 56 17 36 18 92 69 99 27 36 39 10 51 92 73 40 73 27: ѕ38
73 56 56 80 92 67 38 58 17 56 69 58 95 25 56 39 73 46 56 92 17, 80 46 27 23
56 31 24 40 69 39 58 23 80 40 46 40 24 17 56 87 40 73 62 39 87 56 43 58 73ї.
92, 25 56 82 17 56 25 40 69 25 56 25 17 58 38 27 39 73 46 40 99 92 17 27 69
24 67 40 95 73 56 23 56, 38 73 56 67 40 25 40 46 67 92 95 80 56 17 43 58 67
18 80 92 73 58 17 62 67 56 39 73 56 10 73 62 67 40 99 27 82 58 46 58, 80 56
39 73 40 17 95 92 67 43 40 17 92 24 25 46 92 99 92 73 14 82 67 40 80 95 56
17 58 67 56 87 67 56 43 58 67.
Приведем ответ без подробного решения.
Ключ:
| Буква | Число | Буква | Число | Буква | Число | Буква | Число | Буква | Число |
|---|---|---|---|---|---|---|---|---|---|
| а | 40 | ж | 43 | м | 87 | т | 73 | ы | 14 |
| б | 18 | з | 24 | н | 67 | у | 27 | ь | 92 |
| в | 69 | и | 92 | о | 56 | х | 82 | э | 71 |
| г | 23 | й | 31 | п | 25 | ц | 51 | ю | 36 |
| д | 80 | к | 95 | р | 46 | ч | 38 | я | 10 |
| е | 58 | л | 17 | с | 39 | ш | 99 |
Ответ:
О Н И Б Е С Ш У М Н О П О Д Н Я Л И С Ь П О У З К О Й К Р У
Т О Й Л Е С Е Н К Е И О К А З А Л И С Ь В С А Л О Н Е - О Б Ш И Р
Н О М, В О В С Ю Д Л И Н У С А М О Л Е Т А. П О С Т О Я Л И, О
Ж И Д А Я, К О Г Д А Г Л А З А П Р И В Ы К Н У Т К Т Е М Н О Т
Е. В С Е В О К Р У Г П Р И Н Я Л О Ч Е Т К И Е О Ч Е Р Т А Н И Я.
П Р И Б О Р О В И П У Л Ь Т О В З Д Е С Ь Б Ы Л О П Р Е В Е Л И
К О Е М Н О Ж Е С Т В О, Г Л А З А Р А З Б Е Г А Л И С Ь. О Д Н А
К О Б Л А Г О Д А Р Я Т Е М Ж Е Д В У М Н Е Д Е Л Я М Т Р Е Н И
Р О В О К Н А М А К Е Т Е И Т Ы С Я Ч Е К Р А Т Н О П О В Т О Р
Е Н Н Ы М Н А С Т А В Л Е Н И Я М И Н С Т Р У К Т О Р А О Н И С
О В Е Р Ш Е Н Н О Т О Ч Н О З Н А Л И, З А Ч Е М П Р И Ш Л И. П
О Н Я Т И Я Н Е И М Е Л И, Д Л Я Ч Е Г О К О Н К Р Е Т Н О П Р Е
Д Н А З Н А Ч Е Н Ы В С Е Э Т И Ш Т У К И - Н О О Т Н И Х Э Т О
Г О И Н Е Т Р Е Б О В А Л О С Ь.
Н Е П Р О Ш Л О И М И Н У Т Ы, К А К О Н У В И Д Е Л Ц Е Л Ь
И Х Н Е Л Е Г К О Г О И Э К З О Т И Ч Е С К О Г О П У Т Е Ш Е С Т
В И Я - Т Р И П У Л Ь Т А П О П Р А В О М У Б О Р Т У, У С Ы П А Н
Н Ы Е Ч Е Р Т О В О Й У Й М О Й Т У М Б Л Е Р О В, Л А М П О Ч Е
К, П Е Р Е К Л Ю Ч А Т Е Л Е Й И К Н О П О К. Т Р И В Ы П У К Л
Ы Х Э К Р А Н А В В И Д Е В Е Р Т И К А Л Ь Н Ы Х П Р Я М О У Г
О Л Ь Н И К О В - О Н И С А М Ы Е, Н И К А К О Й О Ш И Б К И. . .
Б О Д Р О С Т И Р А Д И, О Н П О В Т О Р И Л П Р О С Е Б Я П О
Л Ю Б И В Ш У Ю С Я Ц И Т А Т У: "Ч Т О О Д И Н Ч Е Л О В Е К
П О С Т Р О И Л, Д Р У Г О Й З А В С Е Г Д А Р А З Л О М А Т Ь С
М О Ж Е Т". И, П О Х Л О П А В П О П Л Е Ч У С Т Р А Ш И Л У В
З Н А К Т О Г О, Ч Т О Н А П А Р Н И К Д О Л Ж Е Н Б Д И Т Е Л Ь
Н О С Т О Я Т Ь Н А Ш У Х Е Р Е, Д О С Т А Л К И Н Ж А Л И З П
Р И Ш И Т Ы Х Н А Д К О Л Е Н О М Н О Ж Е Н.
Следующая задача посвящена криптоанализу текста на русском языке, зашифрованного двумя способами.
Пример 6.7 Для этой задачи образцом послужила [2, задача 6.3] шифробозначения и текст мы заменили). Первый шифртекст получен из исходного текста перестановкой букв. Второй шифртекст получен из того же исходного текста заменой каждой буквы на другую букву так, что разные буквы заменены разными, а одинаковые - одинаковыми. Восстановите исходный текст.
Первый шифртекст:
И Т Ш И Ь О К Т С О Г М А О Ф О К Е Т А П С С Е О Н С С Ы А
В М Ь Ю З Т Ы Т А Ф О Ь В В Б А С О Ж Е З Т С И Н Й А Я Р Р Р
Т О С Н М Я П Н Н О А Т Ш А О В О
Второй шифртекст:
Ф Я Р Ф Р У Ч Р Ф Ц Ы С А Б О В Я О Р Ц А Г Р Ф Ц Р Э Ц Ы Г
Ф И Г Р Х Н Р Ш Ч Д Н В Ц В Т В Н Ч В Ч И Ж Р Ч В Х Д Г В И Ц
Ф Э Ф Ц Р Л Т Р Ф Ц Ы М С А Б О В
Решение. Подсчитаем частоты букв первого шифртекста. Эти частоты будут частотами букв исходного текста, так как первый шифртекст получен перестановкой букв из исходного текста. Одновременно подсчитаем частоты шифробозначений второго текста.
| Первый шифртекст | Второй шифртекст |
|---|---|
| О - 11 | Р - 11 |
| Т, А, С - 8 | Ц, Ф, В - 8 |
| Н - 5 | Ч - 5 |
| В - 4 | Г - 4 |
| И, Ь, М, Е, Р - 3 | Ы, А, О, И, Н - 3 |
| Ш, К, Ф, П, Ы, З, Я - 2 | Я, С, Б, Э, Х, Д, Т - 2 |
| Й, Г, Ю, Б, Ж - 1 | У, Ш, Ж, Л, М - 1 |
Сразу можно сделать вывод: шифробозначению Р соответствует буква О открытого текста, Ч - соответствует Н, а Г - В.
Будем постепенно "проявлять" текст. Запишем второй шифртекст (в нем порядок следования букв не менялся), заменяя уже известные нам шифробозначения их значениями (прописные буквы - это буквы открытого текста, строчные - шифробозначения):
фяОфОуНОфцысабов ...
Далее, шифробозначение Ф скрывает одну из букв: Т, А, С. Шифробозначение Я скрывает либо букву Я, либо согласную. Предположим, что Я Я, пробуем читать начало:
Я, пробуем читать начало:
Не читается. Вывод: Я скрывает согласную, причем одну из следующих: Ш, К, Ф, П, З (вариант Я Ы мы отбросили сразу). Но если Ф
Ы мы отбросили сразу). Но если Ф Т, то слово не читается. Проверим вариант Ф
Т, то слово не читается. Проверим вариант Ф С. Пробуем читать: СяОСОуНОСцы..., и из всех возможных замен для Я подходит только П, тогда начало текста: СПОСОБНОСТЬ, и мы знаем теперь, что Я
С. Пробуем читать: СяОСОуНОСцы..., и из всех возможных замен для Я подходит только П, тогда начало текста: СПОСОБНОСТЬ, и мы знаем теперь, что Я П, У
П, У Б, Ц
Б, Ц Т, Ы
Т, Ы Ь.
Ь.
Обратим внимание на фрагмент ...яорцагрфцрэцы... С учетом наших знаний это: ПоОТаВОСТОэТЬ, и мы находим еще соответствия: О Р, А
Р, А И, Э
И, Э Я. Кроме того, так как Ф
Я. Кроме того, так как Ф С, Ц
С, Ц Т, то из таблицы: В
Т, то из таблицы: В А.
А.
Теперь исследуем последний фрагмент текста: ...фцрлтрфцымсабов. Заменим обозначения их значениями: ...СТОлтОСТЬм... Обратимся к таблице. Обозначению Л соответствует одна из букв Й, Г, Ю, Б, Ж. Пробуем читать, получаем: Л Й, и из таблицы: Т
Й, и из таблицы: Т К. Но тогда М
К. Но тогда М Ю, и слово получилось СТОЙКОСТЬЮ.
Ю, и слово получилось СТОЙКОСТЬЮ.
Теперь начало второй строки: ...АТАКАнНА..., ясно, что Н М. Далее, записываем вторую строку:
М. Далее, записываем вторую строку:
...АТАКАМНАНижОНАхдВАиТСЯСТОЙКОСТЬЮ...
И мы знаем: И Е, Ж
Е, Ж Г, Х
Г, Х З, Д
З, Д Ы.
Ы.
Текст: "Способность шифра противостоять всевозможным атакам на него называется стойкостью шифра".


