Классические шифры

6.8 Комбинированный (композиционный) шифр

Наряду с шифрами перестановки и шифрами замены применяются и шифры, являющиеся комбинацией этих преобразований. Мы представим два варианта комбинированного шифра: поточный шифр и шифр с переменной длиной блока.

Первый алгоритм

Открытый текст, сохраняя пробелы между словами, записывается в таблицу. Начало - в первой строке, текст записывается слева направо, переходя со строки на следующую строку, после чего осуществляется перестановка столбцов. Теперь к каждому столбцу применяется простая замена: каждая буква первого столбца сдвигается циклически вправо на позиций в алфавите, буква второго столбца - на 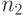позиций, третьего - на 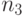позиций, и так дале. Такая замена одну и ту же букву, стоящую в разных столбцах, переводит в разные буквы.

Описанный алгоритм является комбинацией перестановки и замены.

Пример 6.12 Открытый текст записан в таблицу, после чего столбцы переставили в соответствии с ключом зашифрования . На втором этапе буквы первого столбца сдвинули на 1 позицию в алфавите (а б, б в, ...), второго - на 2 позиции, третьего - на 3 позиции, четвертого - на 4 позиции, пятого - на 5 позиций. Расшифровать полученный таким образом шифртекст:

_впфнубжкйцбфёйебххшгжхсу

Решение.

Запишем шифртекст в таблицу:

Зная величины сдвигов на втором этапе зашифрования, для расшифровки выполняем сдвиг -го влево по алфавиту: 1-й столбец - на 1 позицию (а_, ба, и т.д.), 2-й столбец - на 2 позиции, ... . Получаем:

Зная ключ первого этапа зашифрования, осуществляем окончательное расшифрование, применяя обратную подстановку столбцов: . Это даёт нам открытый текст:

армия\_ждет\_всех\_студентов.

6.8.1 Второй алгоритм: комбинированный шифр с переменным размером блока

Блок текста обладает своей структурой, в большей или меньшей степени наследует особенности текстов на естественном языке. Поэтому для рассеяния таковых особенностей по шифртексту и для повышения качества итогового криптопреобразования приходится либо усложнять раундовые операции с блоками либо увеличивать количество раундов.

Можно, однако, для получения хороших показателей диффузии применить и несколько иную идею: работать с блоками переменной длины, менять размер блока от раунда к раунду. Эта идея реализована, например, в [5]. Кратко опишем схему шифрования.

Выбирается достаточно большое составное число . В каждом раунде выполняются преобразования блоков длины 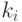, числа 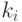-делители . Чередование уменьшения и увеличения длины блока в комбинации с перестановками позволяет добиться сокрытия статистических закономерностей текста за небольшое количество раундов. Здесь мы проиллюстрируем общую схему учебным алгоритмом шифрования с переменной длиной блока, применив замены и перестановку.

• Первое преобразование. Разбиваем текст на биграммы, шифруем каждую биграмму аффинным преобразованием.
• Второе преобразование. Перестановка букв.
• Третье преобразование. Разбиваем текст на триграммы, шифруя каждую с помощью матрицы, проводя вычисления по модулю 33.

Пример 6.13 Первое преобразование: , где - числовой эквивалент шифруемой биграммы. Биграмма АТ имеет эквивалент 0x33+19=19, биграмма ЛА имеет эквивалент 12x33+0=396, биграмма НТ - 14x33+19=481, биграмма ТА - 627. Вычисления дают: Вычисления дают: АТ->17x19+19=342=10x33+12->ЙЛ, ЛА->17x396+19(mod 33²) =6751 (mod 33²)=217=6x33+19->ЁТ, НТ->17x481+19=8196=573=17x33+12->РЛ, ТА->17x627+19=10678=877=26x33+19->ЩТ и после первого преобразования получили тексты: ЙЛЁТРЛ и ЩТЁТРЛ. Второе преобразование: перестановка (462513), получаем: ТЛЛРЙЁ и ТЛТРЩЁ.

Третье преобразование: разбиваем текст на триграммы и шифруем с помощью матрицы . Триграмме ТЛЛ соответствует вектор , результат зашифрования: -> УДЬ, триграмме РЙЁ соответствует вектор , результат зашифрования: -> ДЖР и результатом зашифрования слова АТЛАНТ является шифртекст УДЬДЖР. Проведя вычисления аналогично, получим результат зашифрования слова ТАЛАНТ, это шифртекст ЪШГТЁА.

Итак, АТЛАНТ->УДЬДЖР, ТАЛАНТ->ЪШГТЁА и мы видим, что между результатами зашифрования первого и второго слова нет связи, несмотря на совпадение букв с 3 по 6 в исходных словах. Применение разных типов преобразований к блокам разной длины (в первом преобразовании длина блока 2, во втором 1, в третьем 3) дало хороший результат.