|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Классические шифры
6.10 Разные задачи
Как отмечалось ранее, при решении задач криптоанализа часто бывает необходимо учитывать особенности языка, на котором составлен открытый текст. Полезным является и знание способа перевода буквенного открытого текста в цифровую форму перед шифрованием. Следующие задачи, на наш взгляд, помогут развитию криптоаналитической интуиции.
6.10.1 Задачи, которые условно можно назвать лингвистическими
Пример 6.16 (Составлена по образцу задач 11.3, 12.2, 16.3 из [2) Используется русский алфавит, Е и Ё не различаются. Буквы алфавита кодируются следующим образом: каждой букве ставится в соответствие двоичная запись её номера, начиная с нуля. Таким образом, А соответствует 00000, Б соответствует 00001, В соответствует  . Для передачи используется пять проводов. По каждому передается соответствующий разряд пятизначного двоичного числа. При монтаже 5 проводов были перепутаны, и теперь мы не знаем, по какому проводу приходит цифра старшего разряда и т. д. Перед вами полученный текст. Известно, что исходный текст был осмысленным. Восстановите его. Полученный текст: ЫАДАФЭС
. Для передачи используется пять проводов. По каждому передается соответствующий разряд пятизначного двоичного числа. При монтаже 5 проводов были перепутаны, и теперь мы не знаем, по какому проводу приходит цифра старшего разряда и т. д. Перед вами полученный текст. Известно, что исходный текст был осмысленным. Восстановите его. Полученный текст: ЫАДАФЭС
Решение. Перепутывание проводов не могло изменить количество единиц в двоичной записи буквы. Поэтому вторая и четвертая буквы исходного текста находятся сразу, это буквы А, так как А кодируется как 00000. Первая буква полученного текста Ы. Её код 11011, количество единиц четыре. Запишем буквы с четырьмя единицами в двоичной записи: П, Ч, Э, Ю. Варианты начала слова: ЫА, ПА, ЧА, ЭА, ЮА. Третья буква полученного текста - Д. Её двоичная запись 00100, найдём буквы, имеющие, как и Д, одну единицу в двоичной записи. Это буквы: Б, В, И, Р. Вариант начала ЫА отбросим как невозможный, имеем следующие варианты для первых четырех букв:

Шестая буква полученного текста Э, её код 11101, и есть следующие буквы, коды которых содержат те же четыре единицы: П, Ч, Ы, Ю. Учёт осмысленности исходного текста вариантов для 5 и 7 букв позволяют прочитать: ПАРАШЮТ.
Пример 6.17 Ниже записаны в зашифрованном виде: слева английские слова, справа - их переводы (иногда несколько переводов, но не обязательно все) на русский язык. Английские слова зашифрованы таким образом, что одной и той же букве латинского алфавита соответствует одно и то же число, записанное арабскими цифрами, разным буквам - разные числа. Аналогичным образом, но совершенно независимо, русские слова зашифрованы при помощи последовательности чисел, записанных римскими цифрами.
Буквы одного и того же слова отделены друг от друга запятыми, слова в заданиях - точками с запятой, фразы в заданиях - точками.
Надстрочные знаки и апострофы не учитываются, но и и й считаются разными буквами, а е и ё - не различаются.
| 1 - I |
| 2, 3 - II, III, IV или II, III, I или II, III, V |
| 4, 5, 6 - V, V |
| 7, 8, 9 - VI или VII |
| 8,10 - VIII, V, IX |
| 3, 10, 11 - IX, X или XI, X |
| 7, 12 - XII |
| 2, 10, 12, 4, 5, 6 - II, VII, IX, XIII |
| 13, 6, 1, 5, 8, 9, 14 - XIV, XV, XII, XVI, XIII, I |
Переведите следующие зашифрованные русские слова и фразы в английские:
- XI, III, IX; XIV, XI, V, XV, XIII; XIV, III, II, VII;
- VI, XVI; II, III, XV, I;
- XIV, V, XV, V, XI, XIII, I;
- II, V, VIII, I; XVI, III, XI, XII, IX; IX, III, II.
Решение. Единственное английское слово, состоящее из одной буквы, которое переводится русским словом тоже из одной буквы, - это "я" (1=I; I=я). Единственное русское слово из двух идентичных букв - это ее (её) (4=h, 5=e, 6=r; V=е). Единственное английское слово из трёх букв, переводящееся одним из двух русских слов, каждое из которых состоит из одной буквы, - это and (7=a, 8=n, 9=d; VI=(а или и), VII=(и или а)). Последнее английское слово: 13, r, i, e, n, d, 14, переведённое как XIV, XV, XII, XVI, XIII, я, должно быть friends "друзья" (13=f, 14=s; XII=у, XIII=ь, XIV=д, XV=р, XVI=з). Слово a, 12, переведённое как у, должно быть тогда at (12=t). Слово 2, 10, t, h, e, r, переведённое как II, и/а, IX, ь, - это мать (2=m, 10=o; II=м, VI=и, VII=а, IX=т).
Слова м, III, IV; м, III, я; м, III, е являются переводами одного и того же слова m, 3, которое, очевидно, является словом my (3=y; III=о, IV=й). И, наконец, 8, 10=no, а 3, 10, 11=you (11=u; VIII=н, X=ы, XI=в). Русские слова и фразы, которые нужно перевести, - это:
- Вот дверь дома
- из моря
- деревья
- Меня зовут Том.
6.10.2 Разные задачи
Пример 6.18 ([6]) Алфавит состоит из  букв. Какова максимальная длина слова, если выполнены два условия: а) в нем две рядом стоящие буквы всегда различны; б) из него нельзя получить вычеркиванием букв слова вида
букв. Какова максимальная длина слова, если выполнены два условия: а) в нем две рядом стоящие буквы всегда различны; б) из него нельзя получить вычеркиванием букв слова вида  , где
, где  и
и  - различные буквы?
- различные буквы?
Решение. Если буква встречается только один раз, назовем ее буквой первого рода. В противном случае - буквой второго рода. Буквы, стоящие рядом с буквой второго рода, различны, это следует из свойства "б".
Если слово содержит хотя бы два вида букв, то оно содержит хотя бы одну букву первого рода. В противном случае мы можем получить из него слово вида  , что противоречит условию. Вычеркнув все буквы второго рода, совпадающие с некоторой, получим слово из
, что противоречит условию. Вычеркнув все буквы второго рода, совпадающие с некоторой, получим слово из 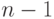 различных букв. Вычеркивая буквы второго рода и далее, придем к слову, состоящему только из букв первого рода.
различных букв. Вычеркивая буквы второго рода и далее, придем к слову, состоящему только из букв первого рода.
Докажем методом математической индукции, что слово имеет длину не более 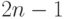 буквы. Для
буквы. Для 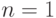 утверждение верно. Предположим теперь, что оно верно для
утверждение верно. Предположим теперь, что оно верно для 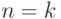 букв и докажем его для
букв и докажем его для  .
.
Пусть слово содержит  различную букву,
различную букву,  - буква первого рода, а
- буква первого рода, а  - соседняя с ней буква. Если
- соседняя с ней буква. Если  - первого рода, то при вычеркивании
- первого рода, то при вычеркивании  возникает слово из
возникает слово из  различных букв, максимальная длина которого не превышает
различных букв, максимальная длина которого не превышает 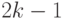 букв (по предположению индукции), а само исходное слово имеет длину не более
букв (по предположению индукции), а само исходное слово имеет длину не более 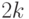 . Если
. Если  - второго рода, то обе соседние буквы пары
- второго рода, то обе соседние буквы пары  ,
,  или различны, или имеется только одна соседняя буква, т. е. пара
или различны, или имеется только одна соседняя буква, т. е. пара 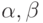 стоит с краю. Поэтому пару
стоит с краю. Поэтому пару 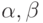 можно вычеркнуть, оставшееся слово удовлетворяет условию "а" задачи. Длина оставшегося слова
можно вычеркнуть, оставшееся слово удовлетворяет условию "а" задачи. Длина оставшегося слова 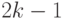 букв, а первоначального -
букв, а первоначального -  .
.
Утверждение доказано. Итак, слово имеет длину не более 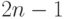 букв.
букв.
Приведем пример слова, имеющего длину в точности 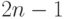 букв. Из алфавита
букв. Из алфавита  можно составить слово
можно составить слово  .
.
Пример 6.19 ([7]) Даны пять правил подстановки:
 ;
; ;
; ;
; ;
;
Правила означают следующее: если в какой-либо последовательности букв можно отыскать левую часть какого-либо из пяти правил, то её разрешается заменить правой частью этого правила и переписать последовательность в новом виде, не меняя остальных букв. После этого можно опять постараться применить какое-либо правило и т. д.
| а) Какие из следующих последовательностей можно получить из буквы D применением какого-либо числа раз правил 1-5: bb, bbc, bbcd, bbcdd, bd, cbd, bdc, b, cdb, cb, cc, ccd, ccdbb, ccccd? |
| б) Охарактеризуйте все последовательности строчных букв, которые могут получиться из буквы D путём применения правил 1-5 и к которым уже нельзя применить ни одного из этих правил. |
Решение. Если применить каждое из пяти правил по одному разу, то получится последовательность cdb. Но вместо того, чтобы использовать правило 5, мы всегда можем снова использовать правило 1, и тогда вместо d появится опять cdb. Это означает, что мы можем получать только следующие циклические последовательности: cdb, ccdbb, cccdbbb и т. д.; каждая такая последовательность описывается следующим образом: c может повторяться сколько угодно раз, потом идёт одно d и столько же раз b, сколько было c.
Пример 6.20 Будем рассматривать последовательности, состоящие только из букв A и B (например, AABABB, AA, B и т. п.). Разрешается преобразовывать каждую из последовательностей следующим образом:
- если в последовательности есть группа BA (подряд и именно в этом порядке), то её можно заменить на ABBB;
- ABBB можно заменить (при тех же условиях) на BA;
- можно вычеркнуть подряд идущую группу AA или BBBB;
- между любыми двумя стоящими рядом буквами последовательности, или левее всех букв, или правее всех букв можно написать группу AA или BBBB.
К каждой последовательности можно применить любое из этих преобразований, к полученной последовательности - снова любое из этих преобразований и т. д.
| а) Какую цепочку преобразований нужно применить к последовательности AB, чтобы получить из неё последовательность BBBA (известно, что это можно сделать)? |
| б) Какую цепочку преобразований нужно применить к последовательностиAB, чтобы получить последовательностьABABAB? |
| в)\textbf{ }Можно ли путём указанных преобразований из последовательности AB получить последовательность ABAB? |
| г)\textbf{ }Докажите, что нельзя путём разрешённых преобразований получить из последовательности AB последовательность BA. |
Решение.
а) AB  BBBBAB BBBBAB  BBBABBBB BBBABBBB  BBBA (сначала слева приписана последовательность BBBB, затем образовавшийся фрагмент BA заменён на ABBB, затем фрагмент ВВВВ в конце образовавшейся последовательности вычеркнут); BBBA (сначала слева приписана последовательность BBBB, затем образовавшийся фрагмент BA заменён на ABBB, затем фрагмент ВВВВ в конце образовавшейся последовательности вычеркнут); |
б) AB  ABAA ABAA  ABAABBBB ABAABBBB  ABABAB (справа приписана последовательность AA, затем справа приписана последовательность BBBB, затем фрагмент ABBB заменён на BA); ABABAB (справа приписана последовательность AA, затем справа приписана последовательность BBBB, затем фрагмент ABBB заменён на BA); |
| в) Нельзя, так как преобразования сохраняют чётность количества A (а также В) в группе букв; |
г) Рассмотрим пару произвольных чисел (x; y), причём  и и  . . |
Придадим буквам A и B смысл операций с парами чисел: A - "заменить знак первого числа на противоположный, второе число оставить без изменений", т. е.  ; B - "поменять числа местами, после чего у числа, оказавшегося на втором месте, поменять знак на противоположный", т. е.
; B - "поменять числа местами, после чего у числа, оказавшегося на втором месте, поменять знак на противоположный", т. е.  .
.
Последовательность из букв A и B будем рассматривать как последовательность выполнения заданных этими буквами операций (в том порядке, как эти буквы записаны).
Очевидно, что последовательности операций AA и BBBB не меняют исходную пару чисел.
Поэтому их можно добавлять или вычёркивать в любом месте последовательности операций, результат от этого не поменяется. Также легко убедиться, что BA и ABBB всегда приводят к одному и тому же результату, т. е. являются взаимозаменяемыми.
То есть, выполняя только разрешённые в условии задачи замены в любой последовательности букв A и B, мы всегда будем получать последовательности операций, в итоге приводящих к одному и тому же результату.
А последовательности операций AB и BA приводят к различным результатам.
Поэтому с помощью разрешённых в условии замен получить из последовательности AB последовательность BA невозможно.
Дополнение. Пару чисел  можно рассматривать как координаты некоторой точки в декартовой прямоугольной системе координат. В этом случае операция A - это осевая симметрия относительно координатной оси Oy, а операция B - это поворот относительно начала координат на
можно рассматривать как координаты некоторой точки в декартовой прямоугольной системе координат. В этом случае операция A - это осевая симметрия относительно координатной оси Oy, а операция B - это поворот относительно начала координат на  по часовой стрелке.
по часовой стрелке.
Тогда A, B порождают группу из 8 элементов: 4 поворотов на углы, кратные прямому, и 4 отражения относительно осей Ox, Oy и биссектрис четвертей, а условия 1)-4) задачи называются порождающими соотношениями этой группы. Каждое из этих преобразований можно ассоциировать с классом эквивалентных слов в алфавите  , где эквивалентными называются слова, получаемые одно из другого применением несколько раз правил 1)-4). В каждом классе можно выбрать представитель. Например, в качестве представителей можно взять: пустое слово (нейтральный элемент группы),
, где эквивалентными называются слова, получаемые одно из другого применением несколько раз правил 1)-4). В каждом классе можно выбрать представитель. Например, в качестве представителей можно взять: пустое слово (нейтральный элемент группы),  ,
,  ,
,  ,
, 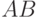 ,
,  ,
,  .
.
Вопрос 4) можно переформулировать на языке теории групп следующим образом: является ли группа 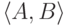 коммутативной? Или, по-другому, лежит ли
коммутативной? Или, по-другому, лежит ли  в классе
в классе 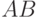 ? Видно, что
? Видно, что  лежит в классе
лежит в классе  .
.
Пример 6.21 (составлен по аналогии с задачей 6.4 из [2]) На каждой из трех осей установлено по одной вращающейся шестеренке и неподвижной стрелке. Шестеренки соединены последовательно. На первой шестеренке 33 зубца, на второй - 10, на третьей - 7. На каждом зубце первой шестеренки по часовой стрелке написано по одной букве русского языка в алфавитном порядке:
А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я.
На зубцах второй и третьей шестеренки в порядке возрастания по часовой стрелке написаны цифры от 0 до 9 и от 0 до 6 соответственно. Когда стрелка первой оси указывает на букву, стрелки двух других осей указывают на цифры. Буквы сообщения шифруются последовательно.
Зашифровывание производится вращением первой шестеренки против часовой стрелки до первого попадания шифруемой буквы под стрелку. В этот момент последовательно выписываются цифры, на которые указывают вторая и третья стрелки. В начале шифрования стрелка 1-го колеса указывала на букву А, а стрелки 2-го и 3-го колес - на цифру 0.
Расшифруйте сообщение 948593312255334486.
Решение. Очевидно, что если начать вращение первой шестерёнки ПРОТИВ часовой стрелки, то вторая начнёт вращаться ПО часовой стрелке, а третья ПРОТИВ часовой стрелки. Шифровалась первая буква. При этом цифра 0 на второй шестерёнке заменена на 9. Замена 0 на 9 могла произойти при повороте второй шестерёнки на 1 позицию или на 11 или на 21, 31. На третьей шестерёнке цифра 0 оказалась заменена на 4. Это могло произойти при повороте на 4 позиции или на 11 или 18 или 25 позиций. Из возможных вариантов для сдвига шестерёнок лишь число 11 является общим. Итак, при шифровании первой буквы произошёл сдвиг на 11 позиций на каждой шестерёнке, в том числе на первой. Таким образом, место под стрелкой заняла буква, отстоящая от А на 11 позиций. Сдвиг на одну позицию заменяет А на Б, сдвиг на две позиции заменит А на В, и т. д. Сдвиг на 11 позиций заменит А на К. Следовательно, первая буква открытого текста - это буква К.
Далее, пара цифр 94 при шифровании второй буквы перешла в 85. Цифра 9 на второй шестерёнке переходит в 8 при повороте на 1 позицию, а также на 11, 21, 31. А цифра 4 на третьей шестерёнке переходит в 5 при повороте на 1, 8, 15, 22, 29. Мы видим, что общим для вариантов сдвига на двух шестерёнках является число 1, и только оно. Вывод: при шифровании второй буквы первая шестерёнка вращалась так, что буква К была заменена на отстоящую от неё на ОДНУ ПОЗИЦИЮ, а это буква Л. И мы знаем первые две буквы открытого текста: КЛ, продолжая рассуждать описанным способом, находим (вычисляем!) все буквы.
Ответ: КЛЮЧШИФРА.







