Классические шифры

6.1 Математические модели открытого текста

([1], §2.5])

Потребность в математических моделях открытого текста продиктована, прежде всего, следующими соображениями. Во-первых, даже при отсутствии ограничений на временные и материальные затраты по выявлению закономерностей, имеющих место в открытых текстах, нельзя гарантировать того, что такие свойства указаны с достаточной полнотой. Например, хорошо известно, что частотные свойства текстов в значительной степени зависят от их характера. Поэтому при математических исследованиях свойств шифров прибегают к упрощающему моделированию, в частности, реальный открытый текст заменяется его моделью, отражающей наиболее важные его свойства. Во-вторых, при автоматизации методов криптоанализа, связанных с перебором ключей, требуется "научить" ЭВМ отличать открытый текст от случайной последовательности знаков. Ясно, что соответствующий критерий может выявить лишь адекватность последовательности знаков некоторой модели открытого текста.

Один из естественных подходов к моделированию открытых текстов связан с учетом их частотных характеристик, приближения для которых можно вычислить с нужной точностью, исследуя тексты достаточной длины. Основанием для такого подхода является устойчивость частот -грамм или целых словоформ реальных языков человеческого общения (то есть отдельных букв, слогов, слов и некоторых словосочетаний). Основанием для построения модели может служить также и теоретико-информационный подход, развитый в работах К. Шеннона.

Учет частот -грамм приводит к следующей модели открытого текста. Пусть 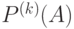представляет собой массив, состоящий из приближений для вероятностей 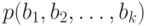появления -грамм 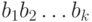в открытом тексте, 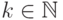, 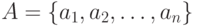- алфавит открытого текста, .

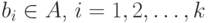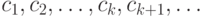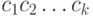Тогда в последовательности знаков алфавита , генерируемой источником "открытого текста", -грамма появляется с вероятностью 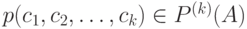, -грамма появляется с вероятность 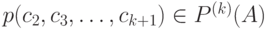. и т. д. Назовем построенную модель открытого текста вероятностной моделью -го приближения.

Таким образом, простейшая модель открытого текста - вероятностная модель первого приближения - представляет собой последовательность знаков 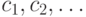, в которой каждый знак , 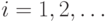появляется с вероятностью , независимо от других знаков. Будем называть также эту модель позначной моделью открытого текста. В такой модели открытый текст 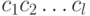имеет вероятность

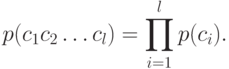
В вероятностной модели второго приближения первый знак 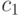имеет вероятность 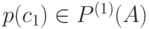, а каждый следующий знак зависит от предыдущего и появляется с вероятностью

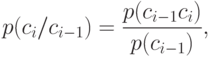
где , , .

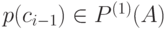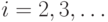Другими словами, модель открытого текста второго приближения представляет собой простую однородную цепь Маркова. В такой модели открытый текст 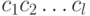имеет вероятность

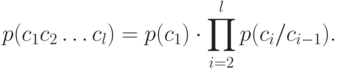
Модели открытого текста более высоких приближений учитывают зависимость каждого знака от большего числа предыдущих знаков. Ясно, что чем выше степень приближения, тем более "читаемыми" являются соответствующие модели.

Отметим, что с более общих позиций открытый текст может рассматриваться как реализация стационарного эргодического случайного процесса с дискретным временем и конечным числом состояний.

6.1.1 Критерии распознавания открытого текста

Заменив реальный открытый текст его моделью, мы можем теперь построить критерий распознавания открытого текста. При этом можно воспользоваться либо стандартными методами различения статистических гипотез, либо наличием в открытых текстах некоторых запретов, таких, например, как биграмма ЪЪ в русском тексте. Проиллюстрируем первый подход при распознавании позначной модели открытого текста.

Итак, согласно нашей договоренности, открытый текст представляет собой реализацию независимых испытаний случайной величины, значениями которой являются буквы алфавита 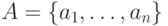, появляющиеся в соответствии с распределением вероятностей 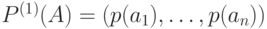. Требуется определить, является ли случайная последовательность 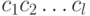букв алфавита открытым текстом, или нет.

Пусть - гипотеза, состоящая в том, что данная последовательность - открытый текст, - альтернативная гипотеза. В простейшем случае последовательность 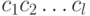можно рассматривать при гипотезе как случайную и равновероятную. Эта альтернатива отвечает субъективному представлению о том, что при расшифровании криптограммы с помощью ложного ключа получается "бессмысленная" последовательность знаков. В более общем случае можно считать, что при гипотезе последовательность 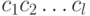представляет собой реализацию независимых испытаний некоторой случайной величины, значениями которой являются буквы алфавита , появляющиеся в соответствии с распределением вероятностей . При таких договоренностях можно применить, например, наиболее мощный критерий различения двух простых гипотез, который дает лемма Неймана-Пирсона.

В силу своего вероятностного характера такой критерий может совершать ошибки двух родов. Критерий может принять открытый текст за случайный набор знаков. Такая ошибка обычно называется ошибкой первого рода, ее вероятность равна 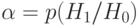. Аналогично вводится ошибка второго рода и ее вероятность . Эти ошибки определяют качество работы критерия. В криптографических исследованиях естественно минимизировать вероятность ошибки первого рода, чтобы не "пропустить" открытый текст. Лемма Неймана-Пирсона при заданной вероятности первого рода минимизирует также вероятность ошибки второго рода.

Критерии на открытый текст, использующие запретные сочетания знаков, например -граммы подряд идущих букв, будем называть критериями запретных -грамм. Они устроены чрезвычайно просто. Отбирается некоторое число редких -грамм, которые объявляются запретными. Теперь, просматривая последовательно -грамму за -граммой анализируемой последовательности 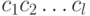, мы объявляем ее случайной, как только в ней встретится одна из запретных -грамм, и открытым текстом в противном случае. Такие критерии также могут совершать ошибки в принятии решения. В простейших случаях их можно рассчитать. Несмотря на свою простоту, критерии запретных -грамм являются весьма эффективными.