|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Инспектор
Вы можете этот курс.
Опубликован: 02.03.2017 | Уровень: для всех | Доступ: платный
Лекция 6:
Классические шифры
6.2 Классификация шифров
(см. также [1, Глава 3])
Большое влияние на развитие криптографии оказали появившиеся в середине XX века работы американского математика Клода Шеннона. В этих работах были заложены основы теории информации, а также был разработан математический аппарат для исследований во многих областях науки, связанных с информацией. Более того, принято считать, что теория информации как наука родилась в 1948 году после публикации работы К. Шеннона "Математическая теория связи".
В своей работе "Теория связи в секретных системах" Клод Шеннон обобщил накопленный до него опыт разработки шифров. Оказалось, что даже в очень сложных шифрах в качестве типичных компонентов можно выделить такие простые шифры как шифры замены, шифры перестановки или их сочетания.
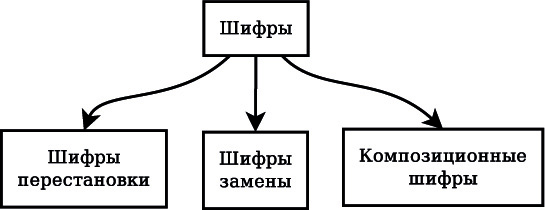
В качестве первичного признака, по которому проводится классификация шифров, используется тип преобразования, осуществляемого с открытым текстом при шифровании. Если фрагменты открытого текста (отдельные буквы или группы букв) заменяются некоторыми их эквивалентами в шифртексте, то соответствующий шифр относится к классу шифров замены. Если буквы открытого текста при шифровании лишь меняются местами друг с другом, то мы имеем дело с шифром перестановки. С целью повышения надежности шифрования шифрованный текст, полученный применением некоторого шифра, может быть еще раз зашифрован с помощью другого шифра.
Всевозможные такие композиции различных шифров приводят к третьему классу шифров, которые обычно называют композиционными шифрами. Заметим, что композиционный шифр может не входить ни в класс шифров замены, ни в класс шифров перестановки ( рис. 6.1 ).
6.3 Шифры перестановки
Шифр перестановки, как видно из названия, осуществляет преобразование перестановки букв в открытом тексте. Типичным примером шифра перестановки является шифр "Сцитала". Обычно открытый текст разбивается на отрезки равной длины и каждый отрезок шифруется независимо. Пусть, например, длина отрезков равна 
и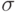 
- взаимнооднозначное отображение множества 
в себя. Тогда шифр перестановки действует так: отрезок открытого текста 
преобразуется в отрезок шифрованного текста.
Классическим примером такого шифра является система, использующая карточку с отверстиями - решетку, которая при наложении на лист бумаги оставляет открытыми лишь некоторые его части. При зашифровке буквы сообщения вписываются в эти отверстия. При расшифровке сообщение вписывается в диаграмму нужных размеров, затем накладывается решетка, после чего на виду оказываются только буквы открытого текста.
Также возможны и другие варианты шифра перестановки, например, шифры столбцовой и двойной перестановки.
6.3.1 Шифр столбцовой перестановки
При расшифровывании буквы шифртекста записываются по столбцам в соответствии с последовательностью чисел ключа, после чего исходный текст считывается по строкам. Для удобства запоминания ключа применяют перестановку столбцов таблицы по ключевому слову или фразе, всем символам которых ставятся в соответствие номера, определяемые порядком соответствующих букв в алфавите.
При решении заданий на криптоанализ шифров перестановки необходимо восстановить начальный порядок следования букв текста. Для этого используется анализ совместимости символов, в чем может помочь таблица сочетаемости (см. [1]).
| Г | С | Слева | Справа | Г | С | |
|---|---|---|---|---|---|---|
| 3 | 97 | л, д, к, т, в, р, н | А | л, н, с, т, р, в, к, м | 12 | 88 |
| 80 | 20 | я, е, у, и, а, о | Б | о, ы, е, а, р, у | 81 | 19 |
| 68 | 32 | я, т, а, е, и, о | В | о, а, и, ы, с, н, л, р | 60 | 40 |
| 78 | 22 | р, у, а, и, е, о | Г | о, а, р, л, и, в | 69 | 31 |
| 72 | 28 | р, я, у, а, и, е, о | Д | е, а, и, о, н, у, р, в | 68 | 32 |
| 19 | 81 | м, и, л, д, т, р, н | Е | н, т, р, с, л, в, м, и | 12 | 88 |
| 83 | 17 | р, е, и, а, у, о | Ж | е, и, д, а, н | 71 | 29 |
| 89 | 11 | о, е, а, и | 3 | а, н, в, о, м, д | 51 | 49 |
| 27 | 73 | р, т, м, и, о, л, н | И | с, н, в, и, е, м, к, з | 25 | 75 |
| 55 | 45 | ь, в, е, о, а, и, с | К | о, а, и, р, у, т, л, е | 73 | 27 |
| 77 | 23 | г, в, ы, и, е, о, а | Л | и, е, о, а, ь, я, ю, у | 75 | 25 |
| 80 | 20 | я, ы, а, и, е, о | М | и, е, о, у, а, н, п, ы | 73 | 27 |
| 55 | 45 | д, ь, н, о, а, и, е | Н | о, а, и, е, ы, н, у | 80 | 20 |
| 11 | 89 | р, п, к, в, т, н | О | в, с, т, р, и, д, н, м | 15 | 85 |
| 65 | 35 | в, с, у, а, и, е, о | П | о, р, е, а, у, и, л | 68 | 32 |
| 55 | 45 | и, к, т, а, п, о, е | Р | а, е, о, и, у, я ,ы, н | 80 | 20 |
| 69 | 31 | с, т, в, а, е, и, о | С | т, к, о, я, е, ь, с, н | 32 | 68 |
| 57 | 43 | ч, у, и, а, е, о, с | Т | о, а, е, и, ь, в, р, с | 63 | 37 |
| 15 | 85 | п, т, к, д, н, м, р | У | т, п, с, д, н, ю, ж | 16 | 84 |
| 70 | 30 | н, а, е, о, и | Ф | и, е, о, а, е, о, а | 81 | 19 |
| 90 | 10 | у, е, о, а, ы, и | X | о, и, с, н, в, п, р | 43 | 57 |
| 69 | 31 | е, ю, н, а, и | Ц | и, е, а, ы | 93 | 7 |
| 82 | 18 | е, а, у, и, о | Ч | е, и, т, н | 66 | 34 |
| 67 | 33 | ь, у, ы, е, о, а, и, в | Ш | е, и, н, а, о, л | 68 | 32 |
| 84 | 16 | е, б, а, я, ю | Щ | е, и, а | 97 | 3 |
| 0 | 100 | м, р, т, с, б, в, н | Ы | Л, х, е, м, и, в, с, н | 56 | 44 |
| 0 | 100 | н, с, т, л | Ь | н, к, в, п, с, е, о, и | 24 | 76 |
| 14 | 86 | с, ы, м, л, д, т, р, н | Э | н, т, р, с, к | 0 | 100 |
| 58 | 42 | ь, о, а, и, л, у | Ю | д, т, щ, ц, н, п | 11 | 89 |
| 43 | 57 | о, н, р, л, а, и, с | Я | в, с, т, п, д, к, м, л | 16 | 84 |
При анализе сочетаемости букв друг с другом следует иметь в виду зависимость появления букв в открытом тексте от значительного числа предшествующих букв. Для анализа этих закономерностей используют понятие условной вероятности.
Систематически вопрос о зависимости букв алфавита в открытом тексте от предыдущих букв исследовался известным русским математиком А.А. Марковым (1856-1922). Он доказал, что появления букв в открытом тексте нельзя считать независимыми друг от друга. В связи с этим А.А. Марковым отмечена еще одна устойчивая закономерность открытых текстов, связанная с чередованием гласных и согласных букв. Им были подсчитаны частоты встречаемости биграмм вида гласная-гласная (г, г), гласная-согласная (г, с), согласная-гласная (с, г), согласная-согласная (с, с) в русском тексте длиной в 
знаков. Результаты подсчета отражены в следующей таблице:
Пример 6.2 [3] Открытый текст, сохраняя пробелы между словами, записали в таблицу. Начало было в первой строке, текст записывали слева направо, переходя со строки на следующую, шифрование заключалось в перестановке столбцов. Найдите открытый текст.
Шифрованный текст:
Решение. Присвоим столбцам номера в порядке их следования. Наша задача - найти такой порядок столбцов, при котором текст будет осмысленным.
Составим таблицу:
Клетка (
, 
) в этой таблице означает, что столбец с номером следует за столбцом с номером . Знаком "Х" отметим невозможные случаи.
Сочетания столбцов 1, 2 и 5, 2 невозможны, так как гласная не может находиться перед мягким знаком. Невозможны и следования столбцов 2, 1 и 2, 5. Теперь из третьей строки следует, что 1, 5 и 5, 1 невозможны, так как УУ - нехарактерная для русского языка биграмма. Далее, два пробела подряд не могут быть в тексте, значит, ставим "Х" в клетках 3, 4 и 4, 3. Снова обратимся к третьей строке. Если бы столбец 2 следовал за столбцом 4, то слово начиналось бы с мягкого знака. Ставим "Х" в клетке 4, 2. Из первой строки: невозможна комбинация 4, 5, невозможна и 3, 5. Итог наших рассуждений представлен в таблице:
Итак, после столбца 6 обязательно следует столбец 5. Но тогда поставим "Х" в клетке 6, 2 и получим: столбец 2 следует за столбцом 3. Далее, мы вычеркнули 5, 1 и 2, 1, следовательно, надо проверить варианты: ...6532... и ...65432... . Но (4, 3) вычеркнуто ранее. Итак, остались варианты расположения столбцов:
- 1, 6, 5, 3, 2, 4
- 6, 5, 3, 2, 4, 1
- 4, 1, 6, 5, 3, 2
- 1, 4, 6, 5, 3, 2
Запишем 6, 5, 3, 2 столбцы подряд:
Попытка поставить столбец 1 перед столбцом 6 приведет к биграмме МП в последней строке и сочетанию ДТЫ в первой. Остались варианты: 653241, 146532.
Ответ: 653241 - ключ, открытый текст: ты\_в\_дороге\_будь\_упрямым (строка из популярной в 1970-е годы песни).
Приведем еще один пример криптоанализа шифра столбцовой перестановки.
Пример 6.3 [1] Расшифровать: СВПООЗЛУЙЬСТЬ\_ЕДПСОКОКАЙЗО
Решение. Текст содержит 25 символов, что позволяет записать его в квадратную матрицу 5х5. Известно, что шифрование производилось по столбцам, следовательно, расшифровывание следует проводить, меняя порядок столбцов.
Необходимо произвести анализ совместимости символов (Таблица сочетаемости букв русского и английского алфавита, а также таблицы частот биграмм представлена выше). В первом и третьем столбце сочетание СП является крайне маловероятным для русского языка. Рассмотрим другие запрещенные и маловероятные сочетания букв: ВП (2,3 столбцы), ПС (3,1 столбцы), ПВ (3,2 столбцы). Перебрав их все, получаем наиболее вероятные сочетания биграмм по столбцам:
Получаем осмысленный текст: ВОСПОЛЬЗУЙТЕСЬ_ПОДСКАЗКОЙ
6.3.2 Шифр двойной перестановки
Пример 6.4 [1] Дан шифртекст: ЫОЕЧТТОУ_СНСОРЧТРНАИДЬН_Е. Известно, что шифрование производилось сначала по столбцам, а затем по строкам.
Решение. Запишем текст в квадратную матрицу 5х5. Расшифровывание следует проводить тем же способом, что и зашифровывание.
Производим анализ совместимости символов. Если в примере столбцовой перестановки можно было легко подобрать нужную комбинацию путем перебора, то здесь лучше воспользоваться таблицей частот букв русского языка (см. приложение). Для оптимизации скорости выполнения задания можно проверить все комбинации букв только в первой строке. Получаем ОЕ-15, ОЧ-12, ЕТ-33, ТЕ-31, ЧО-х, ЕО-7, ЧЫ-х, ОЫ-х, ТЫ-11, ТЧ-1, ЧЕ-23 (где х - запрещенная комбинация).
Теперь необходимо переставить строки в нужном порядке: 3, 2, 4, 5, 1:
Получаем осмысленный текст: СРОЧНО_УСТРАНИТЬ_НЕДОЧЕТЫ
