Самоорганизация (самообучение) нейронных сетей

В простейшем случае пространство ядер совпадает с , а 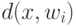- положительно определенная квадратичная форма от , например, квадрат евклидова расстояния. Тогда ядро 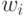, минимизирущее 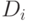, есть центр масс класса :

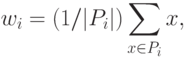
где 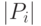- число элементов в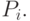

Пусть векторы пространства нормированы. Тогда

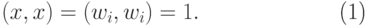( 2)

Так как , то с учетом (2) упрощается решающее правило, разделяющее классы:

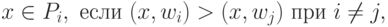
поскольку минимум 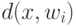достигается при максимуме 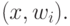Такое решающее правило реализуется с помощью сумматоров, вычисляющих 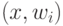, и интерпретатора, выбирающего сумматор с максимальным выходным сигналом. Номер этого сумматора и есть номер класса, к которому относится

Задача поиска ядра 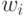для класса превращается в поиск вектора , максимизирующего

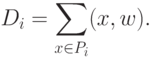
Этот максимум достигается в точке

где - евклидова норма.

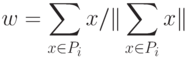
В тех простейших случаях, когда ядро класса точно определяется как среднее арифметическое (или нормированное среднее арифметическое) элементов класса, а решающее правило основано на сравнении выходных сигналов линейных адаптивных сумматоров, нейронную сеть, реализующую метод динамических ядер, называют сетью Кохонена. В определение ядра 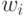для сетей Кохонена входят суммы Это позволит накапливать новые динамические ядра, обрабатывая по одному примеру и пересчитывая 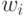после получения в нового примера.

Если число классов заранее не определено, то полезен критерий слияния классов: классы 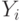и 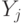сливаются, если расстояние между их ядрами меньше, чем среднее расстояние от элемента класса до ядра в одном из них:

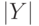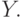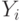где - число элементов в Использовать критерий слияния классов можно так: сначала принимаем гипотезу о достаточном числе классов, строим их, минимизируя , затем некоторые объединяем, повторяем минимизацию с новым числом классов и т.д.