Решение задач комбинаторной оптимизации рекуррентными сетями

Максимизация консенсуса

Переход МБ из одного состояния в другое с максимизацией консенсуса происходит путем выполнения пошаговой процедуры. На каждом ее шаге выполняется испытание, состоящее из двух частей:

1. для данного состояния 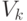генерируется соседнее ,
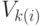2. оценивается, может ли быть принято состояние 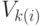, если может, то результат испытания - 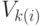, иначе .

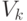Состояние 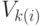принимается с вероятностью

( 4)

где 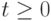- управляющий параметр ("температура").

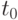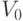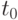Процесс максимизации консенсуса начинается с высокого значения параметра и случайно выбранного начального состояния . В течение процесса параметр уменьшается от до 0. По мере того как приближается к нулю, нейроны все реже изменяют свои состояния, и наконец, МБ стабилизируется в финальном состоянии. Практически, МБ стабилизируется в состоянии, соответствующем локальному максимуму консенсуса, который близок (или равен) глобальному. Сходимостью МБ управляют следующие параметры:

1. Начальное значение параметра для каждого нейрона

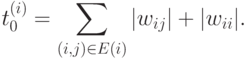
2. Правило понижения

где - положительное число, меньшее единицы, но близкое к ней.

3. Число испытаний, которые проводятся без изменения ( — функция от ).

4. Число последовательных испытаний, не приводящих к изменению состояния машин ( - функция от ), как критерий завершения процесса.

Синхронное и асинхронное функционирование машины Больцмана

Для выполнения синхронного процесса все множество нейронов разбивается на непересекающиеся подмножества , такие, что нейроны, попавшие в одно подмножество, не связаны друг с другом. Тогда на каждом такте синхронизации элементы случайно выбранного подмножества могут одновременно изменять свои состояния в соответствии с заданной вероятностью.

В асинхронном параллельном процессе все нейроны могут изменять свои состояния только в зависимости от величины вероятности. Практически асинхронный параллелизм может быть выполнен следующим образом. Случайно выбирается подмножество , содержащее 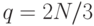нейронов. Для каждого нейрона из этого подмножества устанавливается состояние в соответствии с . Получившееся в результате состояние есть результат одного асинхронного шага.