| Россия, Москва |
Многослойные сети сигмоидального типа
Одномерная оптимизация
Все пошаговые методы оптимизации состоят из двух важнейших частей:
- выбора направления,
- выбора шага в данном направлении (подбор коэффициента обучения).
Методы одномерной оптимизации дают эффективный способ для выбора шага.
В простейшем случае коэффициент обучения фиксируется на весь период оптимизации. Этот способ практически используется только совместно с методом наискорейшего спуска. Величина подбирается раздельно для каждого слоя сети по формуле

где 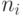 обозначает количество входов
обозначает количество входов  -го нейрона в
слое.
-го нейрона в
слое.
Более эффективный метод основан на адаптивном подборе коэффициента  с учетом фактической
динамики величины целевой функции. Стратегия изменения значения
с учетом фактической
динамики величины целевой функции. Стратегия изменения значения  определяется путем
сравнения суммарной погрешности
определяется путем
сравнения суммарной погрешности  на
на  -й
итерации с ее предыдущим значением,
причем рассчитывается по формуле
-й
итерации с ее предыдущим значением,
причем рассчитывается по формуле
![\varepsilon = [ \sum_{i=1}^M (y_i - d_i)^2]^{1/2}.](/sites/default/files/tex_cache/f5b7e20177308ec84277e91266cc41d6.png)
Для ускорения процесса обучения следует стремиться к непрерывному
увеличению  при
одновременном контроле прироста погрешности
при
одновременном контроле прироста погрешности  по
сравнению с ее значением на
предыдущем шаге. Незначительный рост погрешности считается допустимым.
по
сравнению с ее значением на
предыдущем шаге. Незначительный рост погрешности считается допустимым.
Если погрешности на  -1-й и
-1-й и  -й итерациях
обозначить соответственно
-й итерациях
обозначить соответственно 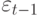 и
и  ,
а коэффициенты обучения на этих же итерациях —
,
а коэффициенты обучения на этих же итерациях — 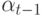 и
и 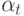 , то значение
, то значение 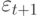 следует рассчитывать по формуле
следует рассчитывать по формуле


где 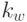 - коэффициент допустимого прироста погрешности,
- коэффициент допустимого прироста погрешности, 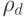 - коэффициент уменьшения
- коэффициент уменьшения  - коэффициент увеличения
- коэффициент увеличения 
Наиболее эффективный, хотя и наиболее сложный, метод подбора коэффициентов
обучения связан с
направленной минимизацией целевой функции в выбранном направлении 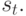 Необходимо так подобрать
значение
Необходимо так подобрать
значение 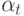 , чтобы новое решение
, чтобы новое решение 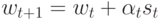 соответствовало минимуму
целевой функции в данном направлении
соответствовало минимуму
целевой функции в данном направлении 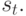
Поиск минимума основан на полиномиальной аппроксимации целевой функции. Выберем для аппроксимации многочлен второго порядка
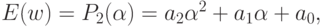
где  ,
,  и
и 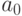 —
коэффициенты, определяемые в цикле оптимизации. Для расчета этих коэффициентов
используем три произвольные точки
—
коэффициенты, определяемые в цикле оптимизации. Для расчета этих коэффициентов
используем три произвольные точки 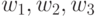 , лежащие в
направлении
, лежащие в
направлении  , т.е.
, т.е.
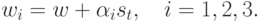
Соответствующие этим точкам значения целевой функции 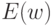 обозначим как
обозначим как
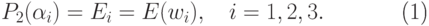 |
( 5) |
Коэффициенты  ,
,  и
и 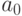 рассчитываются в соответствии с решением системы уравнений (5).
Для определения минимума многочлена
рассчитываются в соответствии с решением системы уравнений (5).
Для определения минимума многочлена 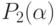 его производная
его производная 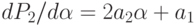 приравнивается к нулю, что
позволяет получить
приравнивается к нулю, что
позволяет получить  . После подстановки выражений для
. После подстановки выражений для 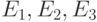 в формулу для
в формулу для  получаем
получаем

![- (\alpha_2 -
\alpha_3)^2(E_2-E_1)]/2[(\alpha_2 - \alpha_1)(E_2-E_3)-(\alpha_2 -
\alpha_3)(E_2-E_1)].](/sites/default/files/tex_cache/f614d3f9b34843dc11fc9ee6db214e1e.png)
