| Россия, Москва |
Задача линейного разделения двух классов
Обучение по всему задачнику
Построим обучающую выборку

В обучающей выборке выделяются все 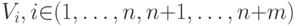 ,
для которых не выполняется неравенство
,
для которых не выполняется неравенство 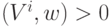 , где
, где  — вектор весовых
коэффициентов нейрона. Обозначим это множество через Err. Вектор
— вектор весовых
коэффициентов нейрона. Обозначим это множество через Err. Вектор  модифицируется только после проверки всей обучающей выборки:
модифицируется только после проверки всей обучающей выборки:
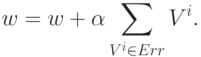
Не требуется хранить все множество Err - достаточно накапливать сумму тех 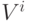 ,
на которых персептрон ошибается:
,
на которых персептрон ошибается:

Как показывают испытания, обучение по всему задачнику, как правило, сходится быстрее, чем обучение по отдельным примерам.
Промежуточный вариант: обучение по страницам
Обучающее множество разбивается на подмножества (страницы) и задается
последовательность прохождения страниц: столько-то циклов по первой странице,
потом
столько-то по второй и т. д. Коррекция вектора  проводится после
прохождения
страницы. Задачник разбивается на страницы по различным эвристическим правилам,
например, по правилу "от простого к сложному". Как показывает
практика, чаще всего
наилучшим является обучение по всему задачнику, иногда (при большом задачнике)
-
обучение по страницам, размеры которых определяются объемом доступной
оперативной
памяти.
проводится после
прохождения
страницы. Задачник разбивается на страницы по различным эвристическим правилам,
например, по правилу "от простого к сложному". Как показывает
практика, чаще всего
наилучшим является обучение по всему задачнику, иногда (при большом задачнике)
-
обучение по страницам, размеры которых определяются объемом доступной
оперативной
памяти.
Геометрическая интерпретация линейного разделения классов
Пусть в нейроне в качестве функции активации используется ступенчатая функция (см. формулу (1) Лекции 2). Линейное разделяющее правило делит входное пространство на две части гиперплоскостью, классифицируя входные векторы как относящиеся к 1-му классу (выходной сигнал - 1) или 2-му классу (выходной сигнал - 0). Критическое условие классификации (уравнение разделяющей гиперплоскости)
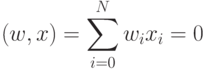
В {  }-мерном пространстве (пространстве входных сигналов)
разделяющая
гиперплоскость перпендикулярна вектору
}-мерном пространстве (пространстве входных сигналов)
разделяющая
гиперплоскость перпендикулярна вектору 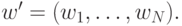 Вектор входных сигналов
Вектор входных сигналов 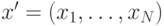 дает выход
дает выход  , если его проекция
, если его проекция 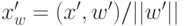 на вектор
на вектор 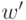 больше, чем расстояние
больше, чем расстояние 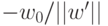 от
нуля до гиперплоскости.
В
от
нуля до гиперплоскости.
В 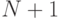 -мерном (расширенном) пространстве гиперплоскость,
описываемая
уравнением
-мерном (расширенном) пространстве гиперплоскость,
описываемая
уравнением 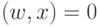 , ортогональна вектору
, ортогональна вектору  и
проходит через начало координат
пространства признаков (образов).
и
проходит через начало координат
пространства признаков (образов).
Пример
В двухмерном пространстве входных сигналов уравнение гиперплоскости имеет вид
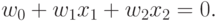
При  и
и 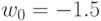 получаем уравнение
получаем уравнение  гиперплоскости, которая представлена на рис.1 пунктирной линией, пересекающей
оси
координат в точках (1.5, 0) и (0, 1.5) соответственно. Здесь:
гиперплоскости, которая представлена на рис.1 пунктирной линией, пересекающей
оси
координат в точках (1.5, 0) и (0, 1.5) соответственно. Здесь: 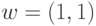 — нормаль к
разделяющей гиперплоскости;
— нормаль к
разделяющей гиперплоскости;  — вектор, относящийся к
первому классу, поскольку
проекция
— вектор, относящийся к
первому классу, поскольку
проекция  вектора
вектора  на нормаль
на нормаль  больше
больше 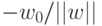 ;
;  — вектор,
относящийся ко второму классу, поскольку
— вектор,
относящийся ко второму классу, поскольку