|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Регрессионная идентификация линейных непрерывных систем управления
Практическая часть
В практической части лабораторной работы будут использовать модели стационарных систем управления. Сигналы входа и выхода будут определяться для известной системы, при этом будем считать, что матрицы  ,
,  уравнения (12.1) и матрицы
уравнения (12.1) и матрицы 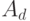 ,
, 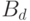 уравнения (12.2) известны. Но для оценки этих матриц будут использоваться только входные воздействия и значения векторов состояния.
уравнения (12.2) известны. Но для оценки этих матриц будут использоваться только входные воздействия и значения векторов состояния.
Пример 1. Произведите регрессионную оценку матриц  ,
,  системы управления, состоящую из последовательного соединения трех инерционных звеньев с параметрами
системы управления, состоящую из последовательного соединения трех инерционных звеньев с параметрами 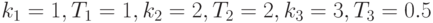 . Входное воздействие на систему примите в виде
. Входное воздействие на систему примите в виде  . Начальное состояние системы примите нулевым по всем переменным состояния.
. Начальное состояние системы примите нулевым по всем переменным состояния.
Изобразим схему объекта управления, представленного через передаточные функции. Схема показана на рис. 12.1.
Связь между входом и выходом, например, первого звена определяется соотношением, выраженным через изображение по Лапласу:
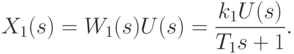
Передаточные функции определены для нулевых начальных условий. Поэтому комплексную переменную s формально можно заменить на производную, т. е.
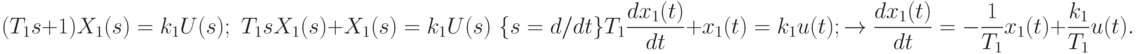
Аналогичные преобразования можно провести для других звеньев. В итоге получим следующую систему дифференциальных уравнений:
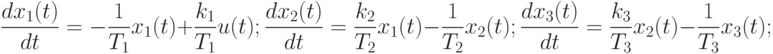 |
( 12.21) |
Систему (12.21) можно представить в матричном виде. Тогда матрицы системы управления будут иметь следующий вид:
![A=
\left[\begin{array}{cccc}
-\frac{1}{T_1}&0&0\\
\frac{k_2}{T_2}&-\frac{1}{T_2}&0\\
0&\frac{k_3}{T_3}&-\frac{1}{T_3}
\end{array}\right],
B=
\left[\begin{array}{cccc}
\frac{k_1}{T_1}\\
0\\
0
\end{array}\right],
C=[0,0,1],D=0.\\](/sites/default/files/tex_cache/36ab2558ec4b74d20fa1e40e8bd0863a.png) |
( 12.22) |
С учетом числовых значений параметров инерционных звеньев будем иметь
![A=
\left[\begin{array}{cccc}
-1&0&0\\
1&-0.5&0\\
0&6&2
\end{array}\right],
B=
\left[\begin{array}{cccc}
1\\
0\\
0
\end{array}\right],
C=[0,0,1],D=0.](/sites/default/files/tex_cache/4abfc263ee7cb19f7abf1ae06cde272e.png) |
( 12.23) |
Программный код решения примера:
function LAB12;
clc,close all
%% Параметры инерционных звеньев
k1 = 1; T1 = 1;
k2 = 2; T2 = 2;
k3 = 3; T3 = 0.5;
%%%------------------------------
%% Матрицы непрерывной системы
global A B
A = [-1/T1, 0, 0;
k2/T2, -1/T2, 0;
0, k3/T3, -1/T3]
B = [k1/T1; 0; 0]
C = [0, 0, 1]
D = 0
%%%------------------------------
%% Размерность системы управления
n = length(A);
%% Размерность управления
r = size(B, 2);
%% Преобразование к дискретной системе
Ts = 0.01; % шаг квантования
%% Расчет матрицы Ad
Ad = expm(A*Ts)
%% Расчет матрицы Bd
if abs(det(A)) < 1e-10
Bd = inv(A)*(Ad - eye(size(A)))*B
else
syms tau
Bd2 = int(expm(-A*tau)*B, tau, 0, Ts);
Bd = double(Bd2)
end
%%%------------------------------
%% Время наблюдений дискретной системы
Kend = 100; %% число шагов квантования
%% Вид входного воздействия
% % U(t) = exp(-0.5*t).*cos(2*t);
%% Решение разностного уравнения
X0 = zeros(length(Ad),1);
Xk = zeros(length(Ad),Kend);
for k = 1 : Kend
sm = zeros(length(Ad), 1);
for J = 0 : k-1
sm = sm + Ad^(k-1-J)*Bd*exp(-0.5*J*Ts)*cos(2*J*Ts);
end
Xk(:,k) = (Ad^k)*X0 + sm;
Uk(1:r,k) = exp(-0.5*k*Ts)*cos(2*k*Ts);
end
%% Хранение массива KSI
KSI = [Xk(:, 2 : end)]';
%% Хранение массива Wk
Wk = [(Xk(:, 1 : end-1))',(Uk(1 : end-1))'];
%% Регрессионная оценка параметров дискретной системы
if abs(det(Wk'*Wk)) < 1e-10
F = (pinv(Wk'*Wk)*Wk'*KSI)';
else
F = (inv(Wk'*Wk)*Wk'*KSI)' ;
end
%% Идентифицированные матрицы
Adr = F(:, 1 : n)
Bdr = F(:, n+1 : end)
%% Обратное преобразование - оценка матриц А, В
global Areg Breg
Areg = logm(Adr)/Ts
if Ts <= 1e-1
Breg = Bdr/Ts
elseif Ts > 1e-1 & abs(det(Areg)) <= 1e-10
Breg = inv(inv(Areg)*(Adr - eye(size(Adr))))*Bdr
else
sd2 = ss(Adr, Bdr, C, D, Ts);
if abs(min(eig(Adr)) ) < 1e-3
sreg = d2c(sd2,'tustin');
else
sreg = d2c(sd2,'zox');
end
[Areg, Breg, C, D] = ssdata(sreg)
end
%%% Верификация модели
%%% Анализ систем при ступенчатом воздействии
global Um
Um = 12;
Xreg0 = zeros(length(Areg), 1);
X0 = zeros(length(A), 1);
T = [0, 12];
[treg, Xreg] = ode23(@fun, T, Xreg0);
[t, X] = ode23(@fun0, T, X0);
h12 = figure(1);
set(h12, 'name','Верификация при ступенчатом воздействии');
line(treg, Xreg, 'linew', 2);
line(t, X,'marker', 'o');
grid on
N = 2*length(Areg);
MN = [ [1:N/2],[1:N/2]]';
str1 = '\bf\it\fontname{times} x\rm\bf_';
str2 = num2str(MN);
str3 = '(\itt\rm\bf)';
legend(strcat(str1, str2, str3), 'location','best');
title('\bf\fontsize{10}\fontname{times}Результат верификации двух моделей систем управления');
xlabel('\bf\fontsize{12}\fontname{times}\it - - - - - - - t - - - - - - -');
ylabel('\bf\fontsize{12}\fontname{times}\it X\rm\bf(\itt\rm\bf) ');
%%%------------------------------
function f = fun0(t,X)
global A B Um
f = A*X + B*Um;
function f = fun(tr, Xr)
global Areg Breg Um
f = Areg*Xr + Breg*Um;В программе преобразование матриц дискретной системы к непрерывной системе может выполняться при ряде условий, в частности, с помощью специализированных функций 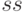 (создание класса объекта – дискретной модели),
(создание класса объекта – дискретной модели),  (преобразование дискретной модели к непрерывной) и
(преобразование дискретной модели к непрерывной) и 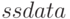 (извлечение матриц системы). В функции
(извлечение матриц системы). В функции  используются методы преобразования
используются методы преобразования  – экстаполятор нулевого порядка,
– экстаполятор нулевого порядка,  – экстраполятор на основе билинейной аппроксимации Тастина [11, 14]. Метод
– экстраполятор на основе билинейной аппроксимации Тастина [11, 14]. Метод  применяется, когда собственные числа матрицы состояния дискретной системы не лежат вблизи нуля комплексной плоскости.
применяется, когда собственные числа матрицы состояния дискретной системы не лежат вблизи нуля комплексной плоскости.
Результат выполнения программы
A =
-1.0000 0 0
1.0000 -0.5000 0
0 6.0000 -2.0000
B =
1
0
0
C =
0 0 1
D =
0
Ad =
0.9900 0 0
0.0099 0.9950 0
0.0003 0.0593 0.9802
Bd =
0.0101
-0.0001
0.0000
Adr =
0.9900 0.0000 -0.0000
0.0099 0.9950 0.0000
0.0003 0.0593 0.9802
Bdr =
0.0101
-0.0001
0.0000
Areg =
-1.0000 0.0000 -0.0000
1.0000 -0.5000 0.0000
0.0000 6.0000 -2.0000
Breg =
1.0050
-0.0050
0.0001
