НОУ ИНТУИТ | Моделирование систем. Лекция 6: Построение интервальных оценок параметров вероятностных распределений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 30.11.2010 | Уровень: специалист | Доступ: платный | ВУЗ: Мордовский государственный университет имени Н.П. Огарева

|

Вам нравится? Нравится 31 студенту

| Поделиться |

Поддержать программу

Аннотация: Цель работы: практически освоить методы построения интервальных оценок для параметров часто используемых вероятностных распределений. Среда программирования — MATLAB.

Ключевые слова: случайная выборка, значение, интервал, равенство, интервальная оценка, коэффициент доверия, доверительная интервальноая оценка, нижняя грница, верхняя граница, случайная величина, длина, доверительный интервал, доверительная вероятность, уровень доверия, функция, место, статистика, оценка математического ожидания

Теоретическая часть

При оценивании неизвестных параметров часто используются интервальные оценки, которые позволяют получить вероятностную характеристику точности оценивания неизвестного параметра. Метод интервальных оценок применяется в случае небольшого числа наблюдений, по которым необходимо произвести оценку параметра [6].

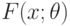Пусть $\vec X_n$ — случайная выборка объема из генеральной совокупности с функцией распределения $F(x;\theta)$ , зависящей от параметра $\theta$ , значение которого неизвестно. Предположим, что для параметра $\theta$ построен интервал $(\theta_i(\vec X_n),\theta_{\hat a}(\vec X_n))$ , где $\theta_i(\vec X_n)$ и $\theta_{\hat a}(\vec X_n)$ являются функциями случайной выборки $\vec X_n$ , такими, что выполняется равенство

$P\{\theta_i(\vec X_n)<\theta <\theta_{\hat a}(\vec X_n)\}=\gamma,$

( 6.1)

В этом случае интервал $(\theta_i(\vec X_n),\theta_{\hat a}(\vec X_n)), где \theta_i(\vec X_n)$ называют интервальной оценкой для параметра $\theta$ с коэффициентом доверия $\gamma$ (или, сокращенно, $\gamma$ - доверительной интервальной оценкой ), а $\theta_i(\vec X_n)$ и $\theta_{\hat a}(\vec X_n)$ , соответственно, нижней и верхней границами интервальной оценки [13].

Интервальная оценка $(\theta_i(\vec X_n),\theta_{\hat a}(\vec X_n)), где \theta_i(\vec X_n)$ представляет собой интервал со случайными границами, который с заданной вероятностью $\gamma$ накрывает неизвестное истинное значение параметра $\theta$ . Таким образом, для различных реализаций случайной выборки $\vec X_n$ статистики $\theta_i(\vec X_n)$ и $\theta_{\hat a}(\vec X_n)$ могут принимать различные значения. При этом вероятностной характеристикой точности оценивания параметра $\theta$ является случайная величина

$\ell(\vec X_n)=\theta_{\hat a}(\vec X_n)-\theta_i(\vec X_n)$

( 6.2)

которая для любой реализации $\vec x_n$ случайной выборки $\vec X_n$ есть длина интервала $(\theta_i(\vec X_n),\theta_{\hat a}(\vec X_n))$ , где $\theta_i(\vec X_n)$ .

Интервал $(\theta_i(\vec X_n),\theta_{\hat a}(\vec X_n)), где \theta_i(\vec X_n)$ называют доверительным интервалом для параметра $\theta$ с коэффициентом доверия $\gamma$ или $\gamma$ - доверительным интервалом.

Наряду с термином "коэффициент доверия" широко используют термины " доверительная вероятность " и " уровень доверия ". При этом коэффициент доверия $\gamma$ чаще всего выбирают равным 0.9, 0.95 или 0.99, т. е. близким к 1.

Построение интервальных оценок осуществляется на основе какой-либо центральной статистики, т. е. такой статистики $T(\vec X_n,\theta)$ , функция распределения которой

$F_T(t)=P\{T(\vec X_n,\theta)<t\}$

( 6.3)

не зависит от параметра $\theta$ [13]. При этом принимаются во внимание следующие предположения:

Функция распределения является непрерывной и возрастающей;
Заданы такие положительные числа $\alpha$ и $\beta$ , что коэффициент доверия $\gamma=1-\alpha-\beta$ ;
Для любой конкретной выборки $\vec x_n$ из генеральной совокупности функция $T(\vec X_n,\theta)$ является непрерывной и возрастающей (убывающей) функцией параметра $\theta$ .

Согласно предположению (допущению) 1, для любого числа $q\in (0,1)$ существует единственный корень h_q уравнения F_T(t)=q , который называют квантилью q функции распределения F_T(t) случайной величины $T(\vec X_n,\theta)$ . Тогда, согласно допущению 2, имеют место равенства

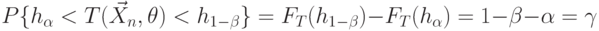
$P\{h_{\alpha}<T(\vec X_n,\theta)< h_{1-\beta}\}=F_T(h_{1-\beta})-F_T(h_{\alpha})=1-\beta-\alpha=\gamma$

которые справедливы для любых возможных значений параметра $\theta$ , т. к. $T(\vec X_n,\theta)$ — центральная статистика и ее функция распределения F_T(t) не зависит от $\theta$ .

Этапы построения доверительного интервала

Построение центральной статистики $T(\vec X_n,\theta)$ с известной функцией распределения.
Представление заданного коэффициента доверия $\gamma$ в виде $\gamma=1-\alpha-\beta$ , т. е. задание уровней значимости (малых величин) $\alpha$ и $\beta$ ;
Нахождение квантилей 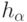$h_{\alpha}$ и $h_{1-\beta}$ уровней $\alpha$ и $\beta$ функции распределения .
Нахождение значений нижней $\theta_i(\vec x_n)$ и верхней $\theta_{\hat a}(\vec x_n)$ границ искомой интервальной оценки путем решения уравнений

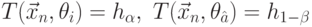
$T(\vec x_n,\theta_i)= h_{\alpha},\mbox{ }T(\vec x_n,\theta_{\hat a})=h_{1-\beta}$

соответственно в случае, когда $T(\vec x_n,\theta)$ — возрастающая функция параметра $\theta$ . Если же $T(\vec x_n,\theta)$ — убывающая функция параметра $\theta$ , то границы интервалов получают путем решения уравнений

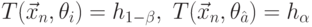
$T(\vec x_n,\theta_i)= h_{1-\beta},\mbox{ }T(\vec x_n,\theta_{\hat a})=h_{\alpha}$

соответственно.

Практическая часть

1. Интервальная оценка параметра экспоненциального распределения

Определение. Случайная непрерывная величина имеет экспоненциальный (показательный) закон распределения с параметром $\lambda$ , если ее плотность вероятности имеет вид

$f(x)=\begin{cases} \lambda e^{-\lambda x},&x\ge0,\\ 0,&x<0. \end{cases}$

( 6.4)

Характеристики экспоненциального распределения

Математическое ожидание:

$M[X]=\frac{1}{\lambda},$

дисперсия:

$D[X]=\frac{1}{\lambda^2},$

Для интервальной оценки параметра экспоненциального распределения вводится центральная статистика вида

$T(\vec X_n,\lambda)=2\lambda n\bar x,$

( 6.5)

где $\bar x =\frac{1}{n}\sum\limits_{i=1}^{n}x_i$ – выборочное среднее реализации $\vec X_n$ .

Статистика (6.5) имеет 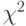$\chi^2$ распределение с степенями свободы. По функции распределения находим квантили для уровней $\alpha$ и $\beta$ , таких, что $\gamma=1-\alpha-\beta$ где $\gamma$ — уровень доверия или доверительная вероятность. Границы доверительного интервала определяются из уравнений (с учетом того, что введенная центральная статистика является возрастающей функцией искомого параметра $\lambda$ ):

$2\lambda_i n \bar x=\chi_{\alpha}^2(2n), \qquad 2\lambda_{\hat a} n \bar x=\chi_{1-\beta}^2(2n),$

( 6.6)

откуда получаем границы доверительного интервала

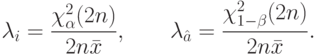
$\lambda_i=\frac{\chi_{\alpha}^2(2n)}{2n \bar x}, \qquad \lambda_{\hat a}=\frac{\chi_{1-\beta}^2(2n)}{2n \bar x}.$

Для моделирования процесса оценки границ доверительного интервала сгенерируем массив случайных чисел , распределенных по экспоненциальному закону с помощью функции exprnd системы MATLAB с заданным параметром — истинным параметром $\lambda$ ( в программе). Для заданного объема выборки случайных чисел рассчитаем среднее выборочное . Для вычисления квантилей применим функцию chi2inv системы MATLAB с степенями свободы. Ввод данных для решения задачи осуществляется интерактивно с помощью диалогового окна inputdlg .

Возможная программная реализация интервальной оценки параметра экспоненциального распределения:

clear,clc,close all
options.Resize = 'on';
options.WindowStyle ='normal';
options.Interpreter = 'tex';  

D = inputdlg({'\bf Введите параметр экспоненциального распределения .......',...
'\bf Введите количество испытаний: ', ...
'\bf введите уровень вероятности a: ',...
'\bf введите уровень вероятности  b: '},...
'Данные задачи по умолчанию',1,...
{' 1.25',' 1000',' 0.01',' 0.04'}, options);
L = str2num(char(D(1)));
n = str2num(char(D(2)));
a = str2num(char(D(3)));
b = str2num(char(D(4)));
pause(0.5)
y = 1-a-b;
x = exprnd(1/L,n,1); %% 1/L - математическое ожидание
m = mean(x); %% среднее значение
a1 = chi2inv(a,2*n); %% обратная функция хи-квадрат
b1 = chi2inv(1-b,2*n);
Ln = a1/(2*n*m);
Lv = b1/(2*n*m);
LL = [Lv Ln];
Dlina = max(LL)- min(LL);
d = 'Доверительная вероятность';
fprintf('\n\tИстинное значение параметра: %g\n ',L)
fprintf('\t%s: %g\n',d,y)
fprintf('\tГраницы доверительного интервала:\n')
fprintf('\t\t\t%s: %g\n', 'нижняя граница', Ln)
fprintf('\t\t\t%s: %g\n', 'верхняя граница',Lv)
fprintf('\tДлина доверительного интервала: %g\n',Dlina)
if L < Ln | L > Lv
fprintf('\n\tИстинное значение параметра не входит в доверительный интервал!\n')
end
%%----------------------- Диаграмма ---------------------
xL = [Ln L];
xLv = [L,Lv];
line([min(xL)-0.2*min(xL) max(xLv)+0.1*max(xLv)],[0 0],'linew',2,'color','k')
line([Ln Ln],[0 1],'linew',2,'linestyle',':')
line([Lv Lv],[0 1],'linew',2,'linestyle',':')
line([L L],[0 1],'color','r','linew',1.5)
 
text(Ln,-0.05,sprintf('%s', '\bf\fontsize{12}\lambda\fontsize{10}_н'))
text(Lv,-0.05, sprintf('%s', '\bf\fontsize{12}\lambda\fontsize{10}_в'))
 text((Ln+Lv)/2,-0.25, sprintf('%s%g', '\bf\fontsize{12}\lambda\fontsize{10}_н = ', Ln))
text((Ln+Lv)/2,-0.35, sprintf('%s%g', '\bf\fontsize{12}\lambda\fontsize{10}_и_c_т = ', L), 'color','r')
text((Ln+Lv)/2,-0.45, sprintf('%s%g', '\bf\fontsize{12}\lambda\fontsize{10}_в = ', Lv))
 
text(min(Ln, Lv),1.1,sprintf('\\bf Интервальная оценка параметра '))
text(min(Ln,Lv),1.03,sprintf('\\bf экспоненциального распределения'))
 
set(gca,'visible','off')
ylim([-0.5 1])
set(gcf,'color','w')

Результат выполнения программы в командном окне MATLAB

Истинное значение параметра: 1.25
 	Доверительная вероятность: 0.95
	Границы доверительного интервала:
			нижняя граница: 1.12687
			верхняя граница: 1.28248
	Длина доверительного интервала: 0.15561

На рис. 6.1 приводится диалоговое окно с параметрами задачи.

Рис. 6.1. Диалоговое окно ввода данных задачи

На рис. 6.2 приведена диаграмма доверительного интервала.

Рис. 6.2. Диаграмма доверительного интервала

Задание 1

Для фиксированных значений входных данных выше приведенной программы рассчитайте частоту попадания истинного значения параметра в доверительный интервал при следующих объемах выборок (в соответствии с номером компьютера):
```
№ 1: n = 100; № 2: n = 200; № 3: n = 300; № 4: n = 400; № 5: n = 500;
№ 6: n = 600; № 7: n = 700; № 8: n = 800;  № 9: n = 900; № 10: n = 1100.
```
Значение $\lambda$ выбрать из интервалов по равномерному закону (в соответствии с номером компьютера):
```
№ 1: (1-1.9); № 2: (0.2-0.29); № 3: (1.3-1.39); № 4: (1.4-1.49); № 5 (1.5-1.59);
№ 6 (1.6-1.69); № 7: (1.7-1.79); № 8: (1.8-1.89); № 9: (1.9-1.99); № 10 (0.35-0.80).
```
Доверительную вероятность $\gamma$ принять равной (в зависимости от номера компьютера):

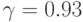№ 1: $\gamma=0.91$ ; № 2: $\gamma=0.92$ ; № 3: $\gamma=0.93$ ; № 4: $\gamma=0.94$ ; № 5: $\gamma=0.95$ ;

№ 6: $\gamma=0.96$ ; № 7: $\gamma=0.97$ ; № 8: $\gamma=0.98$ ; № 9: $\gamma=0.99$ ; № 10: $\gamma=0.995$ .
В графической части обозначения нижней и верхней границ довери-тельного интервала "привяжите" в процентном отношении к этим границам, чтобы исключить возможное наложение надписи с истинным значением параметра $\lambda$ .