|
Добрый день. Я приступила сегодня к самостоятельному изучению курса "Моделирование систем". Хочу понять - необходимо ли отсылать мои решения практических заданий на сайт, (и если да - то где найти волшебную кнопку "Загрузить...") или практические задания остаются полностью на моей совести? (никто не проверяет, и отчётности по ним я предоставлять не обязана?) P.S.: тьютора я не брала |
Оценивание параметров линейной модели по наблюдениям неполного ранга
Теоретическая часть
Пусть линейная модель наблюдений имеет следующий вид в векторно-матричной форме:
 |
( 11.1) |
где:
 — матрица известных коэффициентов порядка
— матрица известных коэффициентов порядка  (матрица регрессоров);
(матрица регрессоров);
 —
—  -мерный вектор неизвестных параметров, подлежащих определению;
-мерный вектор неизвестных параметров, подлежащих определению;
 —
—  -мерный случайный вектор (помехи);
-мерный случайный вектор (помехи);
 — операторы взятия математического ожидания и дисперсии [1].
— операторы взятия математического ожидания и дисперсии [1].
В случае применения метода наименьших квадратов для оценки параметров модели (11.1) приходим к нормальному уравнению
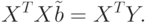 |
( 11.2) |
Если 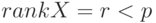 , то информационная матрица
, то информационная матрица  является вырожденной (т. е. ее детерминант равен нулю) и множество решений нормального уравнения (11.2) будет бесконечным [1]. В этом случае модель наблюдений (11.1) называют моделью наблюдений неполного ранга.
является вырожденной (т. е. ее детерминант равен нулю) и множество решений нормального уравнения (11.2) будет бесконечным [1]. В этом случае модель наблюдений (11.1) называют моделью наблюдений неполного ранга.
Оценка общего решения нормального уравнения с вырожденной информационной матрицей может быть получена с помощью обобщенной обратной матрицы, которую обозначают как 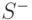 и называют
и называют  -обратной матрицей. Обобщенная обратная матрица всегда существует и не обязательно единственная [1, 17].
-обратной матрицей. Обобщенная обратная матрица всегда существует и не обязательно единственная [1, 17].
Определение. Пусть 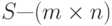 -матрица произвольного ранга. Обобщенной обратной (или
-матрица произвольного ранга. Обобщенной обратной (или  -обратной) матрицей для
-обратной) матрицей для  называется матрица
называется матрица 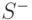 порядка
порядка 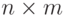 , такая, что
, такая, что
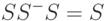 |
( 11.3) |
Нормальное уравнение (11.2) запишем в виде
 |
( 11.4) |
где:
 — квадратная матрица порядка
— квадратная матрица порядка  ;
;
Если 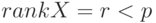 , то матрица
, то матрица  — вырожденная.
— вырожденная.
Общее решение неоднородного уравнения (11.4) есть сумма любого частного решения этого уравнения и общего решения однородного уравнения
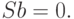 |
( 11.5) |
Известно, что если 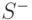 — обобщенная матрица для матрицы
— обобщенная матрица для матрицы  , то частное решение уравнения (11.4) имеет вид
, то частное решение уравнения (11.4) имеет вид
 |
( 11.6) |
Общее решение однородного уравнения (11.5) имеет вид
 |
( 11.7) |
где:
 — произвольный вещественный вектор порядка
— произвольный вещественный вектор порядка  , в том числе и равный тождественно нулю [1].
, в том числе и равный тождественно нулю [1].
Общее решение уравнения (11.4) есть сумма частного решения (11.6) и решения однородного уравнения (11.7), т. е.
 |
( 11.8) |
Алгоритм построения общего решения нормального уравнения и обобщенной обратной матрицы S
- В матрице неполного ранга
 определяют линейно независимые столбцы. Пусть это будут первые
определяют линейно независимые столбцы. Пусть это будут первые  -столбцов.
-столбцов. - Матрицу
 представляют в виде блочной матрицы с подматрицами
представляют в виде блочной матрицы с подматрицами 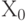 и
и 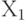 , т. е.
, т. е. ![X = [X_{0}, X_{1}]](/sites/default/files/tex_cache/3a15e2a2cdabb85de5e7da277fdf0a56.png) , где
, где 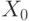 — матрица размера
— матрица размера  .
. - Матрицу
 представляют в виде
представляют в виде![S=X^TX=
\left[\begin{array}{ccc}
X^T_0\\
X^T_1
\end{array}\right]
[X_0,X_1]=
\left[\begin{array}{ccc}
X^T_0X_0 &X^T_0X_1\\
X^T_1X_0 &X^T_1X_1
\end{array}\right].](/sites/default/files/tex_cache/ee6fd2300247d9418c06a8c45caeedf0.png)
- Обобщенную обратную матрицу
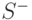 определяют в виде
определяют в виде![S^{-}=
\left[\begin{array}{ccc}
(X^T_0X_0)^{-1}&0\\
0&0
\end{array}\right].](/sites/default/files/tex_cache/c3214745c0e1c7d8a0c60634918b3b20.png)
- Общее решение нормального уравнения — оценку вектора параметров определяют по формуле (11.8) или в следующем виде:
![\hat b=
\left[\begin{array}{ccc}
(X^T_0X_0)^{-1}X^T_0Y\\
0
\end{array}\right]
+
\left[\begin{array}{ccc}
0&(X^T_0X_0)^{-1}X^T_0X_1\\
0&-E_{p-k}
\end{array}\right]z.](/sites/default/files/tex_cache/0c25fbb35b8cea44b2d72bb75339d1e6.png)
- Вычисляют остаточную сумму квадратов RSS (Residual Sum of Squares):


 —
—  — неизвестный
— неизвестный  —
—  —
—  — идемпотентная
— идемпотентная  );
);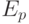 —
— 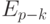 —
—  .
.