НОУ ИНТУИТ | Моделирование систем. Лекция 8: Введение в дисперсионный анализ

Опубликован: 30.11.2010 | Уровень: специалист | Доступ: платный | ВУЗ: Мордовский государственный университет имени Н.П. Огарева

Вам нравится? Нравится 31 студенту

| Поделиться |

Поддержать программу

3. Двухфакторный дисперсионный анализ

Пример 3. В таблице 8.6 представлены результаты наблюдений над откликом на пяти уровнях фактора и четырех уровнях фактора [13]. Требуется проверить на уровне значимости $\alpha = 0.01$ гипотезы:

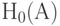$Н_{0}(А)$ — отсутствие влияния фактора на величину отклика ;

$Н_{0}(В)$ — отсутствие влияния фактора на величину отклика .

Предполагается, что взаимосвязь между факторами отсутствует.

В данном примере повторные опыты или наблюдения отсутствуют, по-этому дисперсионный анализ проводится проще, чем это было проведено для общего случая в теоретической части лабораторной работы № 8.

Таблица 8.6.
Данные двухфакторного эксперимента
Уровни фактора	Уровни фактора
Уровни фактора	1	2	3	4	5
1	4	18	26	38	44
2	3	19	25	35	43
3	6	18	24	28	39
4	7	13	21	31	38

Обозначим:

Ар = 5 — число уровней фактора ;

Вр = 4 — число уровней фактора ;

n = 20 — общее число наблюдений (опытов) в эксперименте;

М = [4,18,26,38,44;3,19,25,35,43;6,18,24,28,39;7,13,21,31,38] — матрица эксперимента.

Программный код решения примера:

clear,clc,pause(0.5)
% ВВОД ИСХОДНЫХ ДАННЫХ ЭКСПЕРИМЕНТА
Ap = 5; % ЧИСЛО УРОВНЕЙ ФАКТОРА А
Bp = 4; % ЧИСЛО УРОВНЕЙ ФАКТОРА В
% УРОВЕНЬ ЗНАЧИМОСТИ ПРОВЕРКИ ГИПОТЕЗ
a = 0.01;
% ОБЩЕЕ ЧИСЛО ОПЫТОВ В ЭКСПЕРИМЕНТЕ
n = Ap*Bp;
% МАТРИЦА ЭКСПЕРИМЕНТА
M = [4,18,26,38,44;3,19,25,35,43;6,18,24,28,39;7,13,21,31,38]; 
fprintf('\n\t\t\t ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ\n')
fprintf('\t---------------------------------------------------------\n'); fprintf('\t Число уровней фактора А: Ap = %d\n',Ap)
fprintf('\t Число уровней фактора B: Bp = %d\n',Bp)
fprintf('\t Число опытов в эксперименте: n = %d\n',n)
fprintf('\t Уровень значимости проверки гипотез: a = %1.2f\n',a)
fprintf('\t---------------------------------------------------------\n')
fprintf('\t| Уровни \t\t|\t\t Уровни фактора А(i)\t\t\t|\n')
fprintf('\t| фактора B(j)\t|---------------------------------------|\n')
fprintf('\t|%*s|', 16,''),fprintf('\t%d\t|',1:Ap)
fprintf('\n\t---------------------------------------------------------\n')
Mp = [(1:Bp)',M];
fprintf('\t|\t\t%d\t\t|\t%d\t|\t%d\t|\t%d\t|\t%d\t|\t%d\t|\n',Mp')
fprintf('\t---------------------------------------------------------\n')
% СРЕДНЕЕ ВСЕГО ЭКСПЕРИМЕНТА
Xcp = mean(mean(M));
fprintf('\t Среднее всего эксперимента: Xcp = %g\n',Xcp)
% СРЕДНЕЕ ПО СТРОКАМ МАТРИЦЫ ЭКСПЕРИМЕНТА
Xcmp = mean(M,2);
fprintf('\t---------------------------------------------------------\n')
fprintf('\t Среднее по строкам матрицы эксперимента X.j:\n')
fprintf('\t\t %g',Xcmp)
fprintf('\n')
fprintf('\t---------------------------------------------------------\n')
% СРЕДНЕЕ ПО СТОЛБЦАМ МАТРИЦЫ ЭКСПЕРИМЕНТА
Xcmb = mean(M);

fprintf('\t Среднее по столбцам матрицы эксперимента Xi.:\n')
fprintf('\t\t %g',Xcmb)
fprintf('\n')
fprintf('\t---------------------------------------------------------\n')
% СУММА КВАДРАТОВ ОТКЛОНЕНИЙ ПО ФАКТОРУ А
QA2 = Bp*sum((Xcmb - Xcp).^2);
Na = Ap - 1;
SA2 = QA2/Na;
fprintf('\t Сумма квадратов отклонений по фактору А: QA2 = %g\n',QA2)
fprintf('\t Число степеней свободы фактора А: Na = %g\n',Na)
fprintf('\t Средняя сумма квадратов по числу степеней свободы: SA2 = %g\n',SA2)
fprintf('\t---------------------------------------------------------\n')
% СУММА КВАДРАТОВ ОТКЛОНЕНИЙ ПО ФАКТОРУ В
QB2 = Ap*sum((Xcmp - Xcp).^2);
Nb = Bp - 1;
SB2 = QB2/Nb;
fprintf('\t Сумма квадратов отклонений по фактору В: QB2 = %g\n',QB2)

fprintf('\t Число степеней свободы по фактору В: Nb = %g\n',Nb)
fprintf('\t Средняя сумма квадратов по числу степеней свободы: SB2 = %g\n',SB2)
fprintf('\t---------------------------------------------------------\n')
fprintf('\t\t\t ОШИБКИ\n')
Qo = 0;
for I = 1:Ap
    for J = 1:Bp
        Qo = Qo + (M(J,I) - Xcmb(I) - Xcmp(J) + Xcp)^2;
    end
end
fprintf('\t Ошибка суммы квадратов: Qo = %g\n',Qo)
Nab = Na*Nb;
fprintf('\t Число степеней свободы: Nab = %d\n',Nab)
So2 = Qo/Nab;
fprintf('\t Средняя сумма квадратов ошибки: So2 = %g\n',So2)
fprintf('\t---------------------------------------------------------\n')
Q = 0;
for I = 1:Ap
    for J = 1:Bp
        Q = Q + (M(J,I) - Xcp)^2;
    end
end
fprintf('\t Общая сумма квадратов отклонений: Q = %g\n', Q)
Nq = Ap*Bp - 1;

fprintf('\t Число степеней свободы: Nq = %d\n', Nq)
fprintf('\t--------------------------------------------------\n')
% РАСЧЕТНЫЕ СТАТИСТИКИ ФИШЕРА
fprintf('\t\t РАСЧЕТНЫЕ СТАТИСТИКИ ФИШЕРА\n')
Fa = SA2/So2;
fprintf('\t Статистика по фактору А: Fa = %g\n', Fa)
Fb = SB2/So2;
fprintf('\t Статистика по фактору B: Fb = %g\n', Fb)
fprintf('\t--------------------------------------------------\n')
% КРИТИЧЕСКИЕ ТОЧКИ КРИТЕРИЯ ФИШЕРА
fprintf('\t\t КРИТИЧЕСКИЕ ТОЧКИ КРИТЕРИЯ ФИШЕРА\n')
Ffa = finv(1 - a,Na,Nab);
fprintf('\t Критическая точка по фактору А: Ffa = %g\n', Ffa)
Ffb = finv(1 - a,Nb,Nab);
fprintf('\t Критическая точка по фактору B: Ffb = %g\n', Ffb)
fprintf('\t--------------------------------------------------\n')
% РЕЗУЛЬТАТЫ ДИСПЕРСИОННОГО АНАЛИЗА ПО ПРОВЕРКЕ ГИПОТЕЗ ВЛИЯНИЯ ФАКТОРОВ
fprintf('\n\t РЕЗУЛЬТАТЫ ДИСПЕРСИОННОГО АНАЛИЗА\n')
fprintf('\t ПО ПРОВЕРКЕ ГИПОТЕЗ ВЛИЯНИЯ ФАКТОРОВ\n')
fprintf('\t НА УРОВНЕ ЗНАЧИМОСТИ a = %1.2f\n',a)
% ПРОВЕРКА ФАКТОРА А
if Fa > Ffa
    fprintf('\n\t 1) Гипотезу о влиянии фактора А на отклик следует отвергнуть,\n')
    fprintf('\t\tтак как Fa = %g > Ffa = %g\n', Fa, Ffa)
elseif Fa < Ffa
    fprintf('\n\t 1) Гипотезу о влиянии фактора А на отклик следует принять,\n')
    fprintf('\t\tтак как Fa = %g < Ffa = %g\n', Fa, Ffa)
else
    fprintf('\n\t 1) Гипотезу о влиянии фактора А на отклик следует принять,\n')
    fprintf('\t\tтак как Fa = %g = Ffa = %g\n', Fa, Ffa)
end
% ПРОВЕРКА ФАКТОРА В
if Fb > Ffb
    fprintf('\t 2) Гипотезу о влиянии фактора B на отклик следует отвергнуть,\n')
    fprintf('\t\tтак как Fb = %g > Ffb = %g\n', Fb, Ffb)
elseif Fb < Ffb
    fprintf('\t 2) Гипотезу о влиянии фактора B на отклик следует принять,\n')
    fprintf('\t\tтак как Fb = %g < Ffb = %g\n', Fb, Ffb)
else
    fprintf('\t 2) Гипотезу о влиянии фактора B на отклик следует принять,\n')
    fprintf('\t\tтак как Fb = %g = Ffb = %g\n', Fb, Ffb)
end

Результаты выполнения программы без матрицы данных эксперимента

ДВУХФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
	---------------------------------------------------------
	 Число уровней фактора А: Ap = 5
	 Число уровней фактора B: Bp = 4
	 Число опытов в эксперименте: n = 20
	 Уровень значимости проверки гипотез: a = 0.01
   ………………………………………………………………………………………
	
	 Среднее всего эксперимента: Xcp = 24
	---------------------------------------------------------
	 Среднее по строкам матрицы эксперимента X.j:
		 26		 25		 23		 22
	---------------------------------------------------------
	 Среднее по столбцам матрицы эксперимента Xi.:
		 5		 17		 24		 33		 41
	---------------------------------------------------------
	 Сумма квадратов отклонений по фактору А: QA2 = 3120
	 Число степеней свободы фактора А: Na = 4
	 Средняя сумма квадратов по числу степеней свободы: SA2 = 780
	---------------------------------------------------------
	 Сумма квадратов отклонений по фактору В: QB2 = 50
	 Число степеней свободы по фактору В: Nb = 3
	 Средняя сумма квадратов по числу степеней свободы: 
      SB2 = 16.6667
	---------------------------------------------------------
			 ОШИБКИ
	 Ошибка суммы квадратов: Qo = 80
	 Число степеней свободы: Nab = 12
	 Средняя сумма квадратов ошибки: So2 = 6.66667
	---------------------------------------------------------
	 Общая сумма квадратов отклонений: Q = 3250
	 Число степеней свободы: Nq = 19
	---------------------------------------------------------
		 РАСЧЕТНЫЕ СТАТИСТИКИ ФИШЕРА
	 Статистика по фактору А: Fa = 117
	 Статистика по фактору B: Fb = 2.5
	---------------------------------------------------------
		 КРИТИЧЕСКИЕ ТОЧКИ КРИТЕРИЯ ФИШЕРА
	 Критическая точка по фактору А: Ffa = 5.41195
	 Критическая точка по фактору B: Ffb = 5.95254
	---------------------------------------------------------
	 РЕЗУЛЬТАТЫ ДИСПЕРСИОННОГО АНАЛИЗА
	 ПО ПРОВЕРКЕ ГИПОТЕЗ ВЛИЯНИЯ ФАКТОРОВ
	 НА УРОВНЕ ЗНАЧИМОСТИ a = 0.01

	 1) Гипотезу о влиянии фактора А на отклик следует отверг-нуть,
		так как Fa = 117 > Ffa = 5.41195
	 2) Гипотезу о влиянии фактора B на отклик следует принять,
		так как Fb = 2.5 < Ffb = 5.95254

Задание 3

В соответствии с номером компьютера (1, 2, 3, ...) напишите программы в MATLAB по решению приводимых ниже примеров, когда требуется проверить гипотезы о влиянии фактора и фактора на отклик , а также гипотезы, когда влияние взаимодействия факторов будет значимым.

Компьютер № 1: при уровне значимости $\alpha = 0.1$

x11=abs(11*normrnd(1,1,4,5));x12=abs(11*normrnd(1,1,4,5));x13=abs(11*normrnd(1,1,4,5));
% Матрица данных эксперимента при m = 3 повторных опытах
M = cat(3,x11,x12,x13)

Компьютер № 2: при уровне значимости 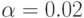$\alpha = 0.02$

x11=abs(12*normrnd(2,1,5,6));x12=abs(12*normrnd(3,1,5,6));x13=abs(12*normrnd(4,1,5,6));
% Матрица данных эксперимента при m = 3 повторных опытах
M = cat(3,x11,x12,x13)

Компьютер № 3: при уровне значимости $\alpha = 0.03$

x11=abs(13*normrnd(3,1,6,7));x12=abs(13*normrnd(4,1,6,7));x13=abs(13*normrnd(5,1,6,7));
% Матрица данных эксперимента при m = 3 повторных опытах
M = cat(3,x11,x12,x13)

Компьютер № 4: при уровне значимости 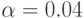$\alpha = 0.04$

x11=abs(14*normrnd(4,.1,8,6));x12=abs(13*normrnd(5,.4,8,6));x13=abs(13*normrnd(6,.8,8,6));
% Матрица данных эксперимента при m = 3 повторных опытах
M = cat(3,x11,x12,x13)

Компьютер № 5: при уровне значимости 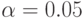$\alpha = 0.05$

x11=abs(15*normrnd(1,.5,5,4));x12=abs(15*normrnd(1,.6,5,4));
x13=abs(15*normrnd(1,.7,5,4)); x14=abs(15*normrnd(1,.8,5,4));  
% Матрица данных эксперимента при m = 4 повторных опытах
M = cat(4,x11,x12,x13,x14)

Компьютер № 6: при уровне значимости 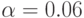$\alpha = 0.06$

x11=abs(16*normrnd(2,1,6,4));x12=abs(16*normrnd(3,1,6,4));
x13=abs(16*normrnd(4,1,6,4)); x14=abs(16*normrnd(1,.8,6,4));  
% Матрица данных эксперимента при m = 4 повторных опытах
M = cat(4,x11,x12,x13,x14)

Компьютер № 7: при уровне значимости $\alpha = 0.07$

x1=abs(17*normrnd(7,.7,7,5));x2=abs(17*normrnd(8,.72,7,5));
x3=abs(17*normrnd(9,.73,7,5)); x4=abs(17*normrnd(10,2,7,5));
x5=abs(17*normrnd(11,1,7,5));  
% Матрица данных эксперимента при m = 4 повторных опытах
M = cat(4,x1,x2,x3,x4,x5)

Компьютер № 8: при уровне значимости $\alpha = 0.08$

x1=abs(18*normrnd(8,1,8,6));x2=abs(18*normrnd(9,1,8,6));
x3=abs(18*normrnd(10,1,8 ,6));x4=abs(18*normrnd(11,1,8,6)); 
x5=abs(18*normrnd(12,1,8,6));  x6=abs(18*normrnd(13,1,8,6));
% Матрица данных эксперимента при m = 4 повторных опытах
M = cat(4,x1,x2,x3,x4,x5,x6)

Компьютер № 9: при уровне значимости $\alpha = 0.09$

x11=abs(9*normrnd(1,1,4,5));x12=abs(9*normrnd(1,1,4,5));x13=abs(9*normrnd(1,1,4,5));
% Матрица данных эксперимента при m = 3 повторных опытах
M = cat(3,x11,x12,x13)

Компьютер № 10: при уровне значимости $\alpha = 0.01$

x11=abs(10*normrnd(2,1,5,6));x12=abs(10*normrnd(3,1,5,6));x13=abs(10*normrnd(4,1,5,6));
% Матрица данных эксперимента при m = 3 повторных опытах
M = cat(3,x11,x12,x13)

Примечание. Матрица данных эксперимента — многомерная матрица, которая представляет собой данные повторных опытов или наблюдений.

Контрольные вопросы

Что такое факторы в дисперсионном анализе?
С какой целью применяют дисперсионный анализ?
Что такое многофакторный дисперсионный анализ?
Что называется факторной дисперсией в дисперсионном анализе?
Что такое остаточная дисперсия в дисперсионном анализе?
Как производится проверка значимости влияния фактора?
В каком случае влияние качественного фактора на выходную переменную отсутствует?
Как рассчитывается несмещенная оценка выборочной дисперсии?

Дальше >>

Моделирование систем

Моделирование систем

Введение в дисперсионный анализ

3. Двухфакторный дисперсионный анализ

Контрольные вопросы

Вопросы и ответы

Студенты

Авторизоваться

Моделирование систем

Моделирование систем

Введение в дисперсионный анализ

3. Двухфакторный дисперсионный анализ

Контрольные вопросы

Вопросы и ответы

Студенты