Функция байесовского риска
Введем обозначение ci для возможных в модели
испытаний (17.7), (17.8) значений отношения правдоподобия:
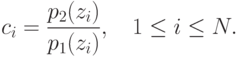 |
(
18.10)
|
Дополним эти значения величинами
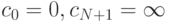 |
(
18.11)
|
и условимся, что
нумерация чисел (18.10), (18.11)
выполнена в порядке возрастания их значений, т.е.
 |
(
18.12)
|
Поскольку при такой нумерации из включения  вытекает выполнение неравенств
вытекает выполнение неравенств
то проверке по
отношению правдоподобия с константой сравнения
c
соответствует
критическая область Q1(i), содержащая
первые
i исходов из
множества (17.7). Т.е.
 |
(
18.13)
|
Таким образом,
класс всех проверок по
отношению правдоподобия
(и, следовательно,
класс всех
байесовских решающих функций) определяется
набором, содержащим
N+1 критическую область:
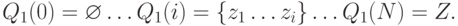 |
(
18.14)
|
Теперь для конкретного значения w, определяющего функцию потерь
из (18.1), вычислим вероятности 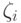 из (18.2), при которых
величина
из (18.2), при которых
величина  из (18.3) совпадает с числом ci из
(18.10), т.е.
из (18.3) совпадает с числом ci из
(18.10), т.е.
Отсюда
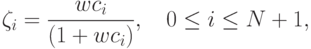 |
(
18.15)
|
причем, в силу (18.11), (18.12),
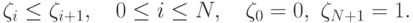 |
(
18.16)
|
Таким образом, интервал [0,1) возможных значений априорной
вероятности 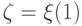 появления первого состояния природы разбивается
значениями из набора (18.15), (18.16) на N+1
подынтервал
появления первого состояния природы разбивается
значениями из набора (18.15), (18.16) на N+1
подынтервал 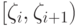 ,
,  . При
этом из включения
. При
этом из включения  вытекает справедливость неравенств
вытекает справедливость неравенств
и, следовательно,
критическая область 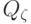
байесовского
критерия
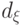
совпадает с
критической областью Q1(i)
из (18.13), т.е.
 |
(
18.17)
|
Согласно (18.1), потери статистика происходят лишь в случае ошибочных решений.
Следовательно, математическое ожидание потерь, соответствующих критерию d,
характеризуемому критической областью Q1 и вероятностями
ошибок (18.6), (18.7), определяется величиной
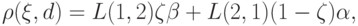 |
(
18.18)
|
где

из (18.2).
Согласно (18.6) и (18.7), критической области (18.17)
соответствуют вероятности ошибок первого и второго рода,
представляющие собой следующие суммы:
 |
(
18.19)
|
 |
(
18.20)
|
Теперь из (18.18)-(18.20) следует, что величина
 |
(
18.21)
|
соответствует ожидаемым потерям для байесовского критерия.
Согласно (18.21), байесовский риск 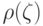 является
кусочно-линейной функцией параметра
является
кусочно-линейной функцией параметра  ,
поскольку значения коэффициентов
,
поскольку значения коэффициентов 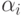 и
и 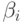 из (18.19) и (18.20)
остаются неизменными при вариации
из (18.19) и (18.20)
остаются неизменными при вариации  в подынтервале
в подынтервале  .
Непосредственной проверкой можно
убедиться, что функция
.
Непосредственной проверкой можно
убедиться, что функция 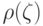 является непрерывной,
поскольку линейные дуги (18.21)
пересекаются в точках
является непрерывной,
поскольку линейные дуги (18.21)
пересекаются в точках 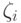 ,
, 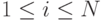 .
Действительно, положим
.
Действительно, положим
и подставим в это
выражение значения вероятностей ошибок
из (18.19), (18.20). В результате получим равенство
совпадающее, согласно (18.10), с определением (18.15)
2.
Отметим также, что из (18.14) и (18.19)-(18.21) можно получить оценки
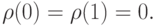 |
(
18.22)
|
Продолжим изучение свойств
байесовского риска.
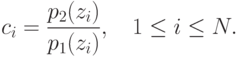
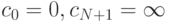

 вытекает выполнение неравенств
вытекает выполнение неравенств

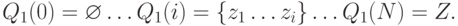
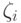 из (18.2), при которых
величина
из (18.2), при которых
величина  из (18.3) совпадает с числом ci из
(18.10), т.е.
из (18.3) совпадает с числом ci из
(18.10), т.е.
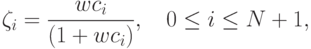
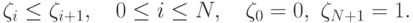
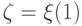 появления первого состояния природы разбивается
значениями из набора (18.15), (18.16) на N+1
подынтервал
появления первого состояния природы разбивается
значениями из набора (18.15), (18.16) на N+1
подынтервал 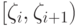 ,
,  . При
этом из включения
. При
этом из включения  вытекает справедливость неравенств
вытекает справедливость неравенств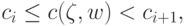
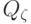 байесовского
критерия
байесовского
критерия 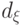 совпадает с критической областью Q1(i)
из (18.13), т.е.
совпадает с критической областью Q1(i)
из (18.13), т.е.
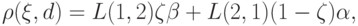
 из (18.2).
из (18.2).


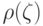 является
кусочно-линейной функцией параметра
является
кусочно-линейной функцией параметра  ,
поскольку значения коэффициентов
,
поскольку значения коэффициентов 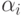 и
и 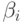 из (18.19) и (18.20)
остаются неизменными при вариации
из (18.19) и (18.20)
остаются неизменными при вариации  в подынтервале
в подынтервале  .
Непосредственной проверкой можно
убедиться, что функция
.
Непосредственной проверкой можно
убедиться, что функция 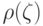 является непрерывной,
поскольку линейные дуги (18.21)
пересекаются в точках
является непрерывной,
поскольку линейные дуги (18.21)
пересекаются в точках 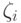 ,
, 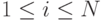 .
Действительно, положим
.
Действительно, положим
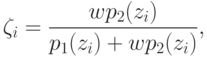
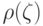 является вогнутой, из чего автоматически
следует ее непрерывность. Тем не менее, небольшое упражнение
по непосредственной проверке непрерывности риска
является вогнутой, из чего автоматически
следует ее непрерывность. Тем не менее, небольшое упражнение
по непосредственной проверке непрерывности риска 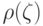 представляется уместным с методической точки зрения..
Отметим также, что из (18.14) и (18.19)-(18.21) можно получить оценки
представляется уместным с методической точки зрения..
Отметим также, что из (18.14) и (18.19)-(18.21) можно получить оценки