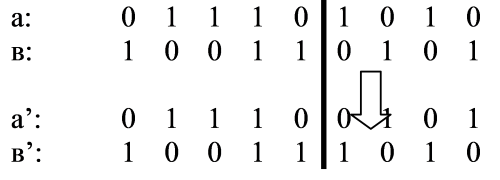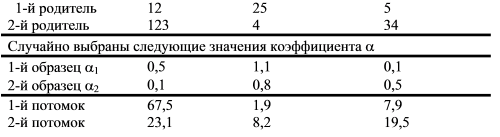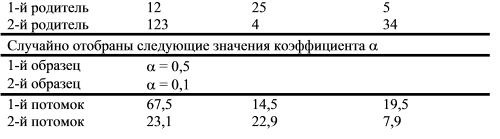НОУ ИНТУИТ | Эволюционные вычисления. Лекция 3: Модификации генетических алгоритмов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 10.10.2014 | Уровень: для всех | Доступ: платный | ВУЗ: Московский государственный университет путей сообщения

|

Вам нравится? Нравится 18 студентам

| Поделиться |

Поддержать программу

3.3. Операторы рекомбинации (скрещивания, кроссинговера)

Различают операторы двоичной и вещественной рекомбинации (скрещивания). Рассмотрим сначала более привычную (и уже знакомую нам), применяемую в простом ГА двоичную рекомбинацию.

3.3.1. Двоичная рекомбинация

3.3.1.1. Одноточечный кроссинговер

Здесь случайным образом выбирается точка скрещивания с вероятностью 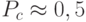$P_c\approx 0,5$ и производится обмен фрагментами хромосом после точки скрещивания. Пример показан на рис.3.8.

Рис. 3.8. Одноточечный кроссинговер

3.3.1.2. Многоточечный кроссинговер

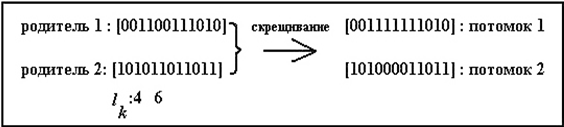
Разработаны различные обобщения классического одноточечного кроссинговера, которые наиболее полно представлены в [2,4].При двухточечном кроссинговере потомки наследуют фрагменты хромосом родителей между двумя случайно выбранными точками скрещивания, как это, например, показано на рис. 3.9

Рис. 3.9. Пример двухточечного кроссинговера

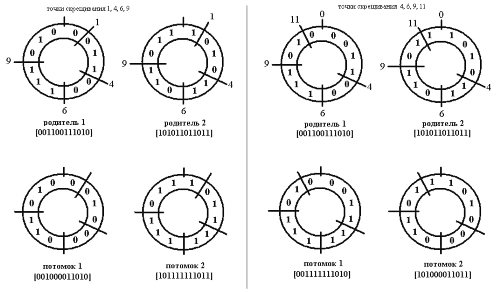
Графически это пример удобно представить в виде, показанном на рис. 3.10. Многоточечный кроссинговер является обобщением предыдущих операторов на случай большего числа точек скрещивания. Например, трехточечный кроссинговер представлен на рис. 3.11.

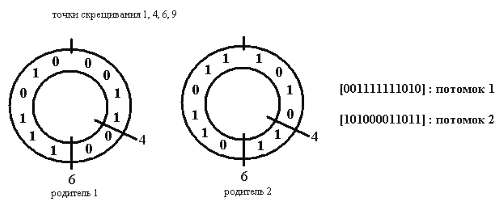
Многоточечный кроссинговер с большим четным количеством точек скрещивания графически удобно представить для хромосом в виде "колец", что показано на рис. 3.12 [1,4]. При этом хромосома рассматривается как замкнутое кольцо, а точки скрещивания выбираются с равной вероятностью по всей его окружности. Например, на рис. 3.10 обмен производится фрагментами между 4-й и 6-й точек скрещивания родительских особей, что также иллюстрируется на рис. 3.11.

Рис. 3.10. Пример двухточечного кроссинговера

Рис. 3.11. Пример трехточечного кроссинговера

Рис. 3.12. Пример четырехточечного кроссинговера

Кроссинговер с нечетным количеством точек скрещивания можно представить таким же способом, если добавить дополнительную точку скрещивания в нулевой позиции.

3.3.1.3. Однородный кроссинговер

Этот вид скрещивания радикально отличается от предыдущих видов. Здесь каждый ген потомка создается путем копирования соответствующего гена из первого или второго родителя, то есть каждая позиция потенциально является точкой кроссинговера.

Для этого случайным образом генерируется двоичная маска кроссинговера той же длины (с тем же числом бит), что у хромосом родителей. Четность бита маски показывает родителя, из которого копируется ген потомка. Для определенности допустим, что 1 соответствует первому родителю, а 0 – второму. На рис. 3.13 показана схема выполнения этого типа кроссинговера на конкретном примере. Каждый бит потомка копируется из 1-го или 2-го родителя в соответствии со значением этого бита маски.

Рис. 3.13. Однородный кроссинговер

Таким образом, потомок содержит смесь генов из каждого родителя.

3.3.1.4. Ограниченный кроссинговер

В этом виде скрещивания точки кроссинговера могут выбираться только там, где значения генов у родителей различны.

3.3.2. Рекомбинация действительных значений

При этом хромосома представляется действительными (вещественными) числами.

3.3.2.1. Дискретная рекомбинация

Этот вид скрещивания определен над векторами, компонентами которых являются вещественные числа. Рассмотрим это на примере двух особей, соответствующие вектора которых имеют три целых значения. Для каждой переменной (позиции) значение переменной выбирается из первого или второго родителя с равной вероятностью. Пример выполнения этого оператора показан на рис. 3.14. Здесь образцы (маски) показывают принадлежность данной компоненты потомка определенному родителю. Отметим, что этот тип рекомбинации применим к значениям любого типа.

3.3.2.2. Промежуточная рекомбинация

Этот метод применим только для особей, представленных только вещественными значениями. Здесь значения потомков строятся в окрестности или между значениями родителей.

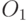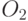В случае промежуточной рекомбинации потомки O_1 и O_2 формируется следующим образом:

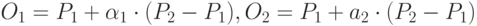$O_1=P_1+\alpha_1\cdot(P_2-P_1),O_2=P_1+a_2\cdot(P_2-P_1)$

( 3.5)

Рис. 3.14. Дискретная рекомбинация

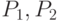где P_1,P_2 – вещественные значения, представляющие первого и второго родителя;

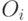O_i – вещественное значение, представляющее потомка;

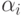$\alpha_i$ - масштабирующий множитель, который выбирается случайным образом из отрезка [-d, 1+d] .

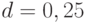При обычной промежуточной рекомбинации d=1 и $\alpha_i\in[0,1]$ . Для обобщенной промежуточной рекомбинации d>0 , обычно полагают d=0,25 . Значение каждой переменной, в том числе и для векторов, формируется по приведенному выражению. Отметим, что здесь используются чисто арифметические операции (сложение и умножение). Заметим, что при 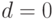d=0 потомки принадлежат отрезку [P_1,P_2] . Эти операторы совершенно не похожи на классический кроссинговер. Фактически, этот оператор заимствован из другого направления эволюционных вычислений - "эволюционных стратегий". На рис. 3.15 показан пример выполнения этого оператора для тех же данных, которые использовались в предыдущем примере.

Рис. 3.15. Промежуточная рекомбинация

Для примера подробно приведем выполнение оператора для 1-ой компоненты

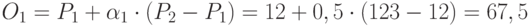$O_1=P_1+\alpha_1\cdot(P_2-P_1)=12+0,5\cdot (123-12)=67,5$

( 3.6)

3.3.2.3 Линейная рекомбинация

Этот вид оператора аналогичен предыдущему, за исключением того, что значение масштабирующего множителя $\alpha$ одинаково для всех переменных (компонент) векторов. Пример выполнения этого оператора представлен на рис.3.16

Рис. 3.16. Линейная рекомбинация

Дальше >>

Эволюционные вычисления

Эволюционные вычисления

Модификации генетических алгоритмов