| Россия, Волгоградская область |
Модификации генетических алгоритмов
3.11.3. Адаптация на основе нечетких контроллеров
Недавно в [21] предложен новый метод адаптации параметров ГА на основе нечетких контроллеров, где баланс между расширением пространства поиска решений и его эксплуатацией реализуется на основе изменения средних значений фитнесс-функции двух последних популяций. В отличие от традиционных методов адаптации в этом методе применяются следующие компоненты:
- Используются три генетических оператора: кроссинговер, иммиграция (разновидность случайного поиска), эвристическая мутация (разновидность эвристического поиска).
- Адаптация значений вероятностей
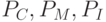 указанных трех генетических операторов
указанных трех генетических операторов 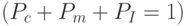 .
.
Эвристическая мутация является разновидностью эвристического поиска. Для этого часто используется LS-техника, которая позволяет генерировать новых потомков из отобранных родителей. Следует отметить, что этот оператор может сдвигать потомков в сторону локального оптимума. Число потомков зависит от вероятности мутации 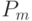 . Фактически значение вероятности мутации определяет вес процесса исследования новых областей в пространстве поиска.
. Фактически значение вероятности мутации определяет вес процесса исследования новых областей в пространстве поиска.
Оператор иммиграции, предложенный в [22], позволяет для некоторых видов функций расширить пространство поиска решений при сохранении того же уровня эксплуатации для популяции данной мощности. Алгоритм модифицируется следующим образом: для каждого поколения включается программа иммиграции особей; генерируются и оцениваются 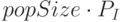 случайных особей; замещаются
случайных особей; замещаются 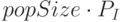 худших особей популяции случайными
худших особей популяции случайными 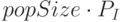 особями, где параметр
особями, где параметр  определяет мощность популяции в процессе эволюции.
определяет мощность популяции в процессе эволюции.
Значения вероятностей иммиграции и кроссинговера определяют вес процесса эксплуатации в пространстве поиска решений. В основной схеме используются два нечетких контроллера: 1) ![T[P_M\wedge(P_C\vee P_M)]](/sites/default/files/tex_cache/4be909e2fa2f9ab7d5a310dccffed90c.png) для адаптивной настройки параметров в процессе расширения и эксплуатации в пространстве поиска 2)
для адаптивной настройки параметров в процессе расширения и эксплуатации в пространстве поиска 2) ![T[P_C\wedge P_I]](/sites/default/files/tex_cache/2bccea20d1f1e770e35c22dfcbde6de9.png) для адаптивного регулирования процесса генетического расширения и случайной эксплуатации, которые реализуются независимо для адаптивного регулирования значений параметров в течение генетического поиска. Для этого используются изменения средних значений фитнесс-функции популяций родителей и потомков в течение u поколений ГА. При этом увеличивается значение
для адаптивного регулирования процесса генетического расширения и случайной эксплуатации, которые реализуются независимо для адаптивного регулирования значений параметров в течение генетического поиска. Для этого используются изменения средних значений фитнесс-функции популяций родителей и потомков в течение u поколений ГА. При этом увеличивается значение  и уменьшается
и уменьшается 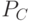 и
и 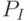 , если происходит улучшение значения фитнесс-функции. И наоборот, уменьшается
, если происходит улучшение значения фитнесс-функции. И наоборот, уменьшается  и увеличивается
и увеличивается 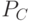 и
и 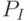 , если у потомков наблюдается ухудшение значения фитнесс-функции. Например, в случае минимизации, мы можем определить изменение среднего значения фитнесс-функции
, если у потомков наблюдается ухудшение значения фитнесс-функции. Например, в случае минимизации, мы можем определить изменение среднего значения фитнесс-функции 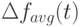 поколения
поколения  следующим образом:
следующим образом:

где  и
и 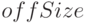 – означают соответственно значения мощности популяций родителей и потомков, удовлетворяющие заданным ограничениям. Регулирование
– означают соответственно значения мощности популяций родителей и потомков, удовлетворяющие заданным ограничениям. Регулирование  определяется с использованием значений
определяется с использованием значений 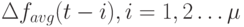 и регулирование
и регулирование 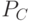 и
и 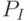 выполняется на основе значений коэффициента корреляции особей текущей популяции следующим образом:
выполняется на основе значений коэффициента корреляции особей текущей популяции следующим образом:
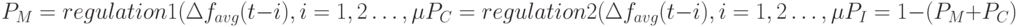
где процедуры regulation 1 и regulation 2 представлены ниже в виде псевдокода.
Функции принадлежности для 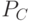 и
и  показаны на рис.3.24 и рис.3.25 соответственно.
показаны на рис.3.24 и рис.3.25 соответственно.
Кроме этого, значения  определяются следующим образом:
определяются следующим образом:
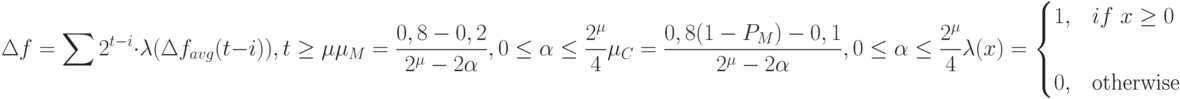
Пусть  и
и 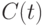 обозначают популяции родителей и потомков соответственно, тогда укрупненный алгоритм адаптивного ГА с нечеткими контроллерами можно представить следующим образом:
обозначают популяции родителей и потомков соответственно, тогда укрупненный алгоритм адаптивного ГА с нечеткими контроллерами можно представить следующим образом: