НОУ ИНТУИТ | Эволюционные вычисления. Лекция 3: Модификации генетических алгоритмов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 10.10.2014 | Уровень: для всех | Доступ: платный | ВУЗ: Московский государственный университет путей сообщения

|

Вам нравится? Нравится 18 студентам

| Поделиться |

Поддержать программу

Контрольные вопросы

Какие методы применяются для генерации начальной популяции?
Какая информация используется при отборе родителей?
Какие недостатки имеет "метод рулетки"?
Чем отличается ранжирование от пропорционального отбора?
Что такое локальный отбор?
Опишите метод турнирного отбора.
Как используется метод Больцмана при отборе особей?
Опишите методы отбора пар для скрещивания.
Что такое неявные методы отбора?
Опишите двоичную рекомбинацию.
Чем отличается многоточечный кроссинговер от классического?
Что такое однородный кроссинговер?
Чем отличается рекомбинация действительных чисел от классического кроссинговера?
Что такое дискретная рекомбинация?
Опишите промежуточную рекомбинацию.
Чем отличается линейная рекомбинация от промежуточной?
Что такое инверсия?
Как выполняется мутация над вещественными числами?
Чем отличается неоднородная мутация от обычной?
Какие существуют методы сокращения популяции?
В каких случаях целесообразно применять генетический микроалгоритм?
Опишите нестационарный ГА.
Чем заменяется отбор родителей в нестационарном ГА?
Какие методы определения сроков жизни вы знаете?
Что такое ниши в ГА?
Чем эволюция Ламарка отличается от эволюции Дарвина?
Опишите гибридный ГА на основе эволюции Ламарка.
В чем заключается адаптация в ГА?
Как изменяются вероятности кроссинговера и мутации при адаптации?
Какие виды адаптации ГА вы знаете?
Как можно выполнить адаптацию числа особей популяции?
Как можно выполнить адаптацию значений вероятностей кроссинговера и мутации.
Опишите адаптивный ГА на основе нечетких контроллеров.

Упражнения

Разработать программу, использующую ГА для нахождения экстремумов (минимумов) функции, согласно таблице вариантов, приведенной в табл.3.2 Программу выполнить на встроенном языке пакета Matlab.
Для функций с числом переменных 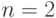вывести на экран график данной функции с указанием найденного экстремума, точек популяции. Для вывода графиков использовать стандартные возможности пакета Matlab. Предусмотреть возможность пошагового просмотра процесса поиска решения.
Повторить нахождение решения с использованием стандартного Genetic Algorithm toolbox. Сравнить полученные результаты.
Исследовать зависимость времени поиска, числа поколений (генераций), точности нахождения решения от основных параметров генетического алгоритма:
- число особей в популяции
- вероятность кроссинговера, мутации.
Критерий остановки вычислений – повторение лучшего результата заданное количество раз или достижение популяцией определенного возраста (например, 100 эпох).
Повторить процесс поиска решения для 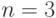, сравнить результаты, скорость работы программы.

Таблица 3.2.
№ вв.	Название	Оптимум	Вид функции
1	De Jong's function 1	global minimum $f(x)=0; x_i=0,\\ I=1:n.$	$f_1(x)=\sum_{i=1}^n x_i^2,\qquad -5,12\le x_i\le 5,12$
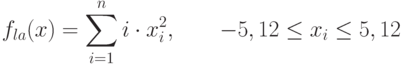2	Axis parallel hyper-ellipsoid function	global minimum $f(x)=0; x_i=0,\\ I=1:n.$	$f_{la}(x)=\sum_{i=1}^n i\cdot x_i^2,\qquad -5,12\le x_i\le 5,12$
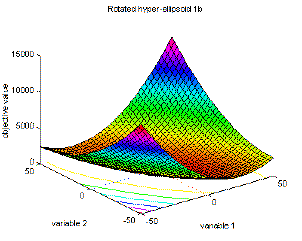
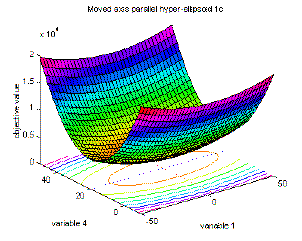
3	Rotated hyper-ellipsoid function	global minimum $f(x)=0; x_i=0,\\ I=1:n.$	$f_{1b}(x)=\sum_{i=1}^n\left(\sum_{j=1}^i x_j\right)^2,\qquad -65,536\le x_i\le 65,536$
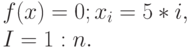
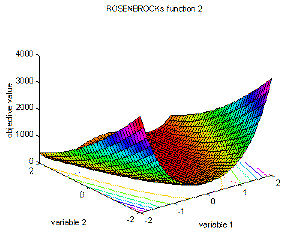
4	Moved axis parallel hyper-ellipsoid function	global minimum $f(x)=0; x_i=5*i,\\ I=1:n.$	$f_{1c}(x)=\sum_{i=1}^n 5i\cdot x_i^2,\qquad -5,12\le x_i\le 5,12$
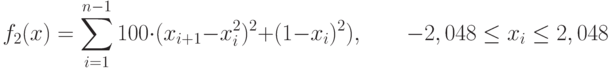5	Rosenbrock's valley (De Jong's function 2)	global minimum $f(x)=0; x_i=0,\\ I=1:n.$	$f_2(x)=\sum_{i=1}^{n-1} 100\cdot (x_{i+1}-x_i^2)^2+(1-x_i)^2),\qquad -2,048\le x_i\le 2,048$
6	Rastrigin's function 6	global minimum $f(x)=0; x_i=0,\\ I=1:n.$	$f_6(x)=10\cdot n+\sum_{i=1}^n(x_i^2-10\cdot \cos(2\cdot\pi\cdot x_i)),\qquad -5,12\le x_i\le 5,12$
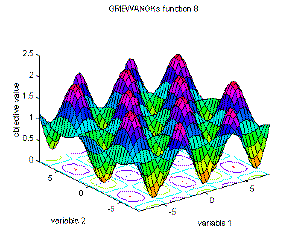
7	Schwefel's function 7	global minimum $f(x)=n\cdot 418.9829; x_i=420.9687,\\i=1:n.$	$f_7(x)=\sum_{i=1}^n -x_i\cdot \sin(\sqrt{\|x_i\|}),\qquad -500\le x_i\le 500$
8	Griewangk's function 8	global minimum $f(x)=0; x_i=0,\\ I=1:n.$	$f_8(x)=\sum_{i=1}^n \frac{x_i^2}{4000}-\prod_{i=1}^n\cos\left(\frac{x_i}{\sqrt{i}\right)+1,\qquad -600\le x_i\le 600$
9	Sum of different power function 9	global minimum $f(x)=0; x_i=0,\\ I=1:n.$	$f_9(x)=\sum_{i=1}^n\|x_i\|^{(i+1)},\qquad -1\le x_i\le 1$
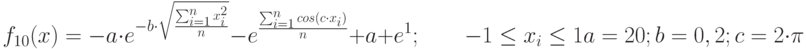10	Ackley's Path function 10	global minimum $f(x)=0; x_i_=0,\\ I=1:n.$	$f_{10}(x)=-a\cdot e^{-b\cdot \sqrt{\frac{\sum_{i=1}^n x_i^2}{n}}}-e^{\frac{\sum_{i=1}^n cos(c\cdot x_i)}{n}}+a+e^1;\qquad -1\le x_i\le 1\\a=20;b=0,2;c=2\cdot \pi$
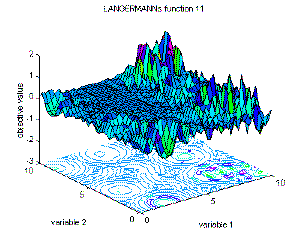
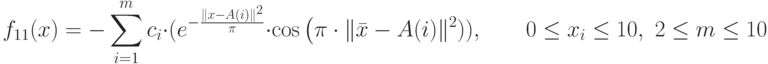11	Langermann's function 11	global minimum $f(x)=-1.4 (for\ m=5); x_i=???,\\i=1:n.$	$f_{11}(x)=-\sum_{i=1}^m c_i\cdot(e^{-\frac{\\|x-A(i)\\|^2}{\pi}}\cdot\cos\left(\pi\cdot\\|\bar x-A(i)\\|^2)),\qquad 0\le x_i\le 10,\ 2\le m\le10$
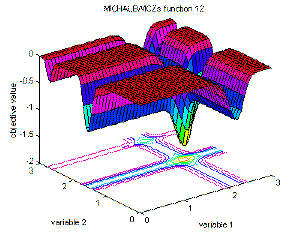
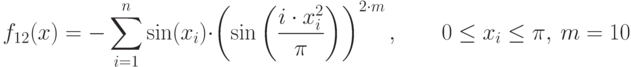12	Michalewicz's function 12	global minimum $f(x)=-4.687 (n=5); x_i=???,\\i=1:n.\\f(x)=-9.66 (n=10); x_i=???,\\i=1:n.$	$f_{12}(x)=-\sum_{i=1}^n \sin(x_i)\cdot\left(\sin\left(\frac{i\cdot x_i^2}{\pi} \right ) \right)^{2\cdot m},\qquad 0\le x_i\le \pi,\ m=10$
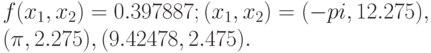
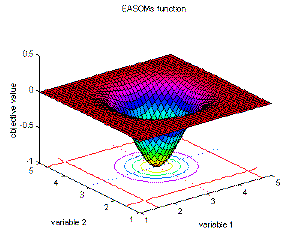
13	Branins's rcos function	global minimum $f(x_1,x_2)=0.397887;(x_1,x_2)=(-pi,12.275),\\ (\pi,2.275), (9.42478,2.475).$	$f_{Bran}(x_1,x_2)=a\cdot(x_2-b\cdot x_1^2+c\cdotx_1-d)^2+e\cdot(1-f)\cdot(x_1)+e,\\ -5\le x_1\le 10,\ 0\le x_2\le \15\\a=1,b=\frac{5,1}{4\cdot \pi^2},c=\frac{5}{\pi},d=6,e=10,f=\frac{1}{8\cdot\pi}$
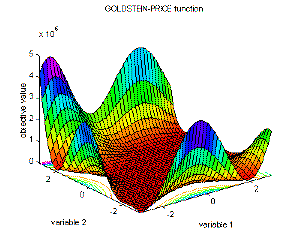
14	Easom's function	global minimum $f(x_1,x_2)=-1;\\(x_1,x_2)=(\pi,\pi).$	$f_{Easo}(x_1,x_2)=-\cos(x_1)\cdot\cos(x_2)\cdot e^{-((x_1-\pi)^2+(x_2-\pi)^2)},\qquad -100\le x_i\le 100$
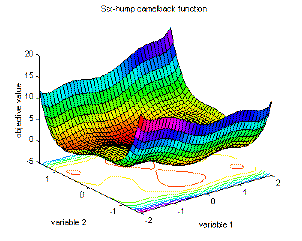
15	Goldstein-Price's function	global minimum $f(x_1,x_2)=3;\\(x_1,x_2)=(0,-1).$	$f_{Gold}(x_1,x_2)=(1+(x_1+x_2+1)^2\cdot(19-14x_1+3x_1^2-14x_2+6x_1x_2+3x_2^2))\\\cdot(30+(2x_1-3x_2)^2\cdot(18-32x_1+12x_1^2+48x_2-36x_1x_2+27x_2^2)),\\ -2\le x_i\le 2$
16	Six-hump camel back function	global minimum $f(x_1,x_2)=-1.0316;\\(x_1,x_2)=(-0.0898,0.7126), (0.0898,-0.7126).$	$f_{Sixh}(x_1,x_2)=(4-2.1\cdot x_1^2+x_1^{4/3})\cdot x_1^2+x1\cdot x_2+(-4+4\cdot x_2^2)\cdot x_2^2;\\ -3\le x_1\le 3,-2\le x_2\le2$

Краткие итоги:

рассмотрены различные модификации и обобщения ГА;
описаны различные виды отбора родительских особей;
показаны разные виды кодирования потенциальных решений;
представлено множество генетических операторов кроссинговера и мутации;
рассмотрены динамические ГА, где в процессе поиска изменяется мощность популяции;
определены ГА на основе ниш для мультимодальных функций;
описаны меметические ГА;
рассмотрены гибридные ГА;
представлены ГА на основе моделирования эволюции Ламарка;
описаны различные виды адаптивных ГА, где при поиске решений изменяются параметры ГА

Дальше >>

Эволюционные вычисления

Эволюционные вычисления