Модификации генетических алгоритмов

3.5. Сокращение промежуточной популяции

Необходимой компонентой является устранение плохих решений, полученных в процессе формирования новой популяции.

3.5.1. Глобальная редукция

Промежуточную популяцию (репродукционную группу) составляют все особи -го поколения и новые особи, полученные в результате скрещивания и мутации. Численность этой популяции можно определить следующим образом

( 3.12)

где: - число особей предыдущей популяции;

– численность особей, полученных путем скрещивания;

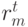– число "мутантов".

Обычно в стационарных ГА мощность популяции поддерживается постоянной . Поскольку , то необходимо устранить неудачные решения. Для этого существуют различные методы редукции.

3.5.1.1. Чистая замена

В простейшем случае с помощью скрещивания и мутации генерируются столько потомков, сколько было родителей. Далее родители устраняются, а потомки формируют следующее поколение . При этом каждая особь живет лишь одно поколение. Такая схема часто используется в простом ГА. Однако при этом очевидно не исключено, что некоторые очень хорошие решения могут быть заменены худшими, и лучшее решение будет потеряно.

3.5.1.2. Элитарная схема

В ней потомков генерируется меньше, чем было родителей. Далее вновь построенные потомки заменяют худших родителей согласно значениям фитнесс-функции. Для этой схемы возможна преждевременная сходимость к локальным экстремумам.

3.5.1.3. Равномерная случайная замена

При таком подходе потомков также генерируется меньше, чем было родителей, далее случайным образом удаляется необходимое число родителей, которые заменяются новыми потомками.

3.5.1.4. Пропорциональная редукция

Здесь потомков генерируется больше, чем необходимо для замены. Далее заменяют заданное число родителей только лучшими потомками согласно значениям фитнесс-функции

3.5.1.5. Селекционная схема

Здесь родители и потомки выступают на равных правах - они помещаются в одну репродукционную группу. В ней все особи этой группы ранжируются и в следующее поколение включаются только лучшие особей. Иногда применяется следующая модификация этого метода. Сначала вычисляется среднее значение ЦФ группы и в следующее поколение включаются те особи, у которых значение ЦФ больше среднего значения группы.

В общем случае к репродукционной группе может быть применен любой метод отбора родителей, которые были рассмотрены в разделе 3.2.

3.5.2. Локальная замена

При локальном отборе особи выбираются из ограниченного окружения множества соседей. Замена особей потомками выполняется по такой же схеме. Таким образом сохраняется локальность информации. При этом используются те же структуры и отношения соседства, что и в разделе 3.2.4.

Родитель особи определяются первым родителем из локального окружения (множества соседей). Для выбора удаляемых родителей и отбора потомков для замены применяются следующие схемы:

• Ввести в новое поколение каждого потомка и заменить случайным образом особи из их окружения;
• Ввести каждого потомка и заменить худшей особью соответственного окружения;
• Ввести потомка лучше, чем худшая особь в окружении, и заменить худшие особи.

3.6. Асинхронные генетические алгоритмы

До сих пор мы рассматривали стационарные синхронные эволюционные алгоритмы, где мощность популяции поддерживается постоянной и переход к следующему поколению "синхронизирован". Здесь обрабатываются все потомки предыдущего поколения, а затем следует переход на следующую итерацию (поколение).

Иногда на практике применяется и асинхронный эволюционный алгоритм, где нет явного разбиения эволюции на поколения, а процесс развития реализуется "по событию" в виде непрерывного потока событий отбора, кроссинговера, мутации и т.п. Здесь вновь порожденные потомки сразу замещают (в некотором смысле худшие) особи (не дожидаясь остальных родительских пар своего поколения). Ниже представлен один из возможных вариантов асинхронного алгоритма реализации ГА с применением турнирного отбора родителей.

0. установка параметров эволюции;
1. инициализация начальной популяции;
2. случайный выбор подмножества особей популяции – участников турнира;
3. оценка фитнесс-значений каждого участника турнира;
4. отбор победителей турнира;
5. выполнение генетических операторов кроссинговера и мутации для победителей;
6. замена проигравших особей потомками победителей;
7. если критерий окончания не выполнен, то переход к п.2;
8. выбор лучшего решения в конечной популяции.

Следует отметить, что такой метод, как правило, проще в реализации (особенно аппаратной) и имеет некоторые преимущества.