|
Пожалуйста, проясните ситуацию. Был выбран курс " Компьютерная алгебра" для самостоятельного изучения. Как теперь записаться на этот курс с целью получения диплома о повышении квалификации? На данный момент он имеет статус " изучаю". Если я пройду экзаменационный тест в таком статусе без оформления документов и оплаты диплома, придется ли еще раз регистрироваться на этот курс и заново проходить тестирование? |
Интегрирование полиномов и рациональных функций. Некоторые сведения из дифференциальной алгебры. Структурная теорема
24.5. ПРИМЕР.
![\int f\,dx = \int \left[ 2xe^{x^2 }\log x +\frac{e^{x^2 }}x+\frac {\log x
-2}{(\log^2 x+x)^2 }
+\frac{\frac 2x\log x +\frac 1x +1}{\log^2 x+x}\right]\,dx.](/sites/default/files/tex_cache/926c80a4e727a748e7c7181cac1e288e.png)
Положим 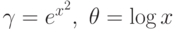 . Структурная теорема
дает возможность проверить,
что
. Структурная теорема
дает возможность проверить,
что  и
и  являются регулярными мономами
над
являются регулярными мономами
над 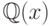 и
и 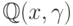 соответственно.
соответственно.
В терминах  ,
,  и
и  подынтегральная функция принимает вид:
подынтегральная функция принимает вид:
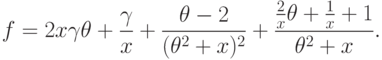
Рассматривая  как рациональную функцию от
как рациональную функцию от  с коэффициентами в поле
с коэффициентами в поле 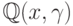 видим, что первые два слагаемых являются полиномами
от
видим, что первые два слагаемых являются полиномами
от  , а последние
два - рациональными функциями. Учитывая, что полином
, а последние
два - рациональными функциями. Учитывая, что полином  абсолютно неприводим
(т. е. неприводим при любом расширением поля констант), будем искать решение в
виде
абсолютно неприводим
(т. е. неприводим при любом расширением поля констант), будем искать решение в
виде
![f=\frac d{dx}\left[ B_2\theta ^2 +B_1\theta +B_0+\frac {B_{11}}{\theta ^2
+x}+c_1\log(\theta ^2 +x)\right],](/sites/default/files/tex_cache/c4f497827a779f9a8a8891c1adddd74c.png)
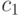 - константа,
- константа, 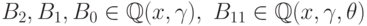 и
линеен по
и
линеен по  . (Это согласуется с теоремой Лиувилля.)
. (Это согласуется с теоремой Лиувилля.)Дифференцируя это соотношение, получим
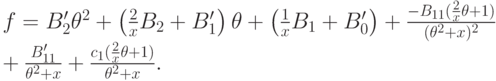
Приравниваем коэффициенты при степенях  , начиная со
старшей. Для полиномиальной части получаем следующие соотношения.
, начиная со
старшей. Для полиномиальной части получаем следующие соотношения.
Приравнивая коэффициенты при 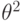 , получаем
, получаем 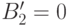 , следовательно,
, следовательно, 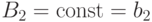 .
.
Приравнивая коэффициенты при  , имеем
, имеем 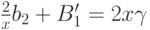 , следовательно,
, следовательно, 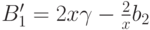 . Интегрируя это
выражение в поле
. Интегрируя это
выражение в поле 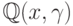 , получаем
, получаем 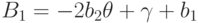 , следовательно,
, следовательно, 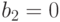 и
и  .
.
Приравнивая слагаемые, не зависящие от  , убеждаемся, что
, убеждаемся, что 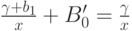 . Следовательно,
. Следовательно, 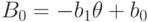 , значит
, значит 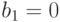 и
и 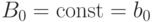 .
.
Разбор рациональной части начинаем со слагаемых с максимальной степенью
знаменателя.
Чтобы избавиться от слагаемых со знаменателем  нужно решить сравнение
нужно решить сравнение
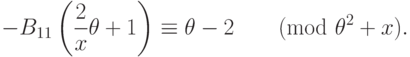
Для нахождения коэффициента 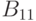 нам нужно в поле
нам нужно в поле 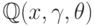 решить уравнение
решить уравнение
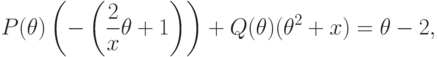
 - линейный относительно
- линейный относительно  полином,
полином,  .
.Получаем 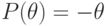 ,
,  , следовательно,
, следовательно,  и
и
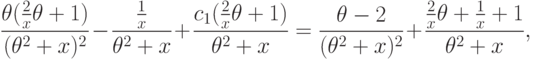
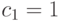 .
.После подстановки всех неизвестных, окончательный результат принимает вид
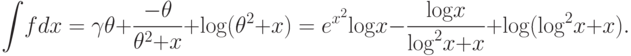
Отметим следующие моменты в рассмотренном примере.
- Мы пользовались абсолютной неприводимостью полинома
 (т. е. его неприводимостью при
произвольном расширении поля констант). Если
знаменатель разлагается на множители (возможно, после расширения поля
констант), то рациональная часть принимает более сложный вид.
(т. е. его неприводимостью при
произвольном расширении поля констант). Если
знаменатель разлагается на множители (возможно, после расширения поля
констант), то рациональная часть принимает более сложный вид. - Возможную форму интеграла мы получали из теоремы Лиувилля.
- Вычисление неопределенных коэффициентов в формуле для интеграла сводилось путем дифференцирования к решению некоторого линейного дифференциального уравнения первого порядка над меньшим полем.
- Подынтегральная функция в меньшем поле зависела от параметров, и
интегрировать ее было возможно только при некоторых ограничениях на параметры
(например,
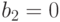 ).
).
В разобранных выше примерах мы видели, что применение метода неопределенных
коэффициентов приводит к задаче нахождения рациональных решений уравнений
более общего вида, чем 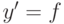 , а именно,
, а именно,

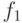 и
и  - известные элементарные функции.
Уравнение (24.1) носит
название уравнения Риша.
- известные элементарные функции.
Уравнение (24.1) носит
название уравнения Риша.