НОУ ИНТУИТ | Введение в компьютерную алгебру. Лекция 11: Интегрирование полиномов и рациональных функций. Некоторые сведения из дифференциальной алгебры. Структурная теорема

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 04.03.2008 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 28 студентам

| Поделиться |

Поддержать программу

23.10. ОПРЕДЕЛЕНИЕ.

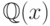$\mathbb Q (x)$ -дифференциальное поле элементарных функций с дифференцированием $\frac d{dx}$ .
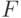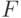Если -дифференциальное поле элементарных функций и $\EuScript F$ -его алгебраическое расширение, то $\EuScript F$ -также дифференциальное поле элементарных функций.
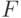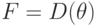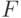Если $\EuScript F$ -дифференциальное расширение дифференциального поля элементарных функций и $\EuScript F =D(\theta )$ , где $\theta$ -либо логарифм, либо экспонента над , то $\EuScript F$ -дифференциальное поле элементарных функций.

Хотя кажется, что это определение накладывает очень сильные ограничения на функции, называемые элементарными, в действительности элементарными является большинство функций, рассматриваемых в курсе математического анализа, в частности, тригонометрические, обратные тригонометрические, гиперболические, обратные гиперболические, как показывают следующие соотношения.

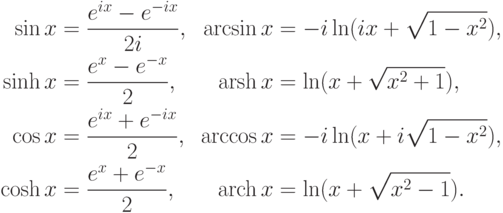
$\begin{align*} \sin x&=\frac {e^{ix}-e^{-ix}}{2i},& \arcsin x&=-i\ln (ix+\sqrt{1-x^2 }),\\ \sinh x&=\frac {e^x-e^{-x}}2,& \arsh x&=\ln (x+\sqrt{x^2 +1}),\\ \cos x&=\frac {e^{ix}+e^{-ix}}2,& \arccos x&=-i\ln (x+i\sqrt{1-x^2 }),\\ \cosh x&=\frac {e^x+e^{-x}}{2},& \arch x&=\ln (x+\sqrt{x^2 -1}). \end{align*}$

Теперь мы можем сформулировать задачу интегрирования в конечном виде.

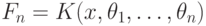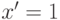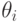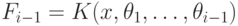
23.11. ЗАДАЧА. Пусть $\EuScript F _n=K(x,\theta_1,\dots,\theta_n)$ -дифференциальное поле, где -конструктивное поле констант (т. е. 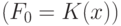предполагается, что мы можем реализовать вычисления в поле на компьютере), - переменная, для которой x'=1 , и для любого от 1 до элемент $\theta_i$ является либо алгебраическим элементом, либо логарифмом, либо экспонентой над полем $\EuScript F _{i-1}= K(x,\theta_1,\dots,\theta _{i-1})$ $(\EuScript F _0 =K(x))$ . 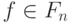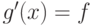Построить алгоритм, позволяющий для произвольной элементарной функции $f\in \EuScript F _n$ найти элементарную функцию g(x) , для которой g'(x)=f , если только такая функция существует.

Естественно возникает вопрос о существовании универсального алгоритма, применимого к любой элементарной функции f(x) .

Как правило, подынтегральная функция зависит не только от переменной интегрирования, но и от некоторых других переменных, которые мы будем называть параметрами. Мы будем предполагать, что на параметры не наложено никаких соотношений. Вычисление неопределенных интегралов от функции, содержащей параметры, можно понимать двумя способами: нахождение формулы, которая представляет собой неопределенный интеграл данной функции при всех значениях параметров, или нахождение множества значений параметров, при которых функция интегрируема и вычисление интеграла для значений параметров из этого множества. Мы будем рассматривать задачу в первой постановке. Вторая постановка чаще всего приводит к неразрешимым задачам. Приведем пример, когда простое подынтегральное выражение во второй постановке задачи интегрирования приводит к очень сложным вопросам.

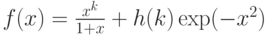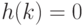23.12. ПРИМЕР. Пусть $f(x)=\frac {x^k}{1+x} + h(k)\exp(-x^2 )$ , где -действительный параметр, а -некоторая функция с действительными значениями. Можно показать, что первое слагаемое интегрируемо тогда и только тогда, когда -рациональное число, а второе -когда h(k)=0 . Кроме того между интегралами слагаемых в этой сумме нет взаимодействия, т. е. сумма интегрируема тогда и только тогда, когда интегрируемо каждое слагаемое. Значит интегрируемость нашего выражения зависит от того, является ли рациональное число корнем уравнения h(y)=0 .

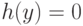Ключевым результатом для обоснования алгоритмов интегрирования в конечном виде является теорема Лиувилля, которую мы приводим без доказательства.

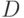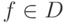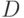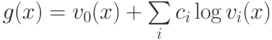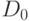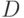23.13. ТЕОРЕМА. Пусть $\EuScript D$ -некоторое дифференциальное поле, - его поле констант и $f\in\EuScript D$ . Пусть g(x) -элементарная над $\EuScript D$ функция, удовлетворяющая уравнению g'(x)=f(x) . 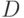Тогда g(x) можно представить в виде $g(x)=v_0(x)+\sum\limits_i c_i \log v_i(x)$ , где c_i -константы из алгебраического замыкания поля , $v_0(x)\in\EuScript D$ , $v_i(x)\in\EuScript D _0$ , где $\EuScript D _0$ - некоторое расширение поля $\EuScript D$ , получающееся присоединением к нему конечного числа констант, алгебраических над $\EuScript D$ .

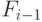Алгоритмы интегрирования имеют рекурсивный характер, когда от задачи, сформулированной в терминах поля $\EuScript F _i$ , нужно перейти к одной или нескольким задачам над полем $\EuScript F _{i-1}$ . При этом существенно различаются методы, используемые для трансцендентных и алгебраических расширений. В данном курсе мы рассмотрим только случай трансцендентных расширений, алгебраические расширения требуют значительно более сложной техники, основанной на фундаментальных результатах алгебраической геометрии.

Прежде чем излагать алгоритм интегрирования трансцендентных функций, рассмотрим несколько примеров.

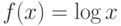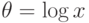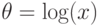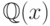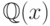23.14. ПРИМЕР. Рассмотрим уравнение g'(x)= f(x) , где $f(x)= \log x$ . Введем обозначение $\theta =\log x$ . Тогда $\theta '=\frac 1x$ , т. е. $\theta =\log (x)$ в наших терминах. Легко видеть, что элемент $\theta$ трансцендентен не только над $\mathbb Q (x)$ , но даже над $\C(x)$ . Будем рассматривать $\theta$ как независимую переменную над основным полем функций $\mathbb Q (x)$ .

Предположим, что интеграл от линейного полинома от переменной $\theta$ должен являться полиномом второй степени от $\theta$ , т. е. должен иметь вид $B_2\theta ^2 +B_1\theta +B_0$ , где $B_i\in \mathbb Q (x)$ .

Задача интегрирования приняла вид уравнения

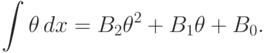
$\int \theta\,dx = B_2\theta ^2 +B_1\theta +B_0.$

Дифференцируя по , получим

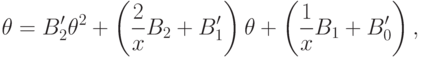
$\theta =B_2'\theta ^2 +\left(\frac 2x B_2+B_1'\right)\theta +\left(\frac 1xB_1+B_0'\right),$

где

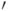обозначает дифференцирование по

. Приравняв коэффициенты при одинаковых степенях переменной $\theta$ в правой и левой частях уравнения, мы получим систему трех линейных обыкновенных неоднородных дифференциальных уравнений:

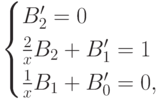
$\begin{cases} B_2'=0&\\ \frac 2xB_2+B_1'=1& \\ \frac 1xB_1+B_0'=0,&\end{cases}$

которая равносильна системе

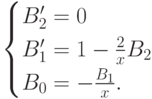
$\begin{cases} B_2'=0&\\ B_1'=1-\frac 2xB_2& \\ B_0=-\frac {B_1}x.&\end{cases}$

Решение каждого из этих уравнений сводится к интегрированию некоторой функции. При этом нужно помнить, что мы ищем неизвестные функции из поля 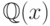$\mathbb Q (x)$ . Интегрированием неизвестные функции B_i определяются с точностью до констант (констант интегрирования). Значения этих констант (кроме последней) однозначно определяются следующим уравнением в выписанной системе. 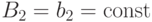Из первого уравнения получаем $B_2=b_2=\const$ . Подставляя это значение во второе уравнение, после интегрирования получаем ограничения на константу b_2 :

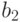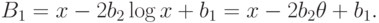
$B_1=x-2b_2\log x+b_1=x-2b_2\theta +b_1.$

Учитывая, что функция B_1

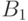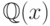должна принадлежать полю $\mathbb Q (x)$ , получаем однозначно определенное значение константы b_2

:

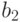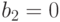. Таким образом,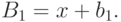

Последнее уравнение принимает вид

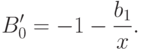
$B_0'=-1 -\frac{b_1}x.$

Интегрируя его, получаем

$B_0=-x -b_1\theta +b_0.$

Откуда

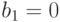и

.

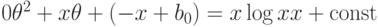Таким образом, мы определили функции B_i с точностью до единственной константы b_0 , значение которой не может быть определено условием задачи. Непосредственной проверкой убеждаемся, что полученное выражение $0\theta ^2 +x\theta +(-x+b_0)=x\log x x + \const$ является решением исходного уравнения. Заметим, что в данном случае нам не требуется обосновывать выбор формы решения и трансцендентность элемента $\theta$ . Если предъявлена функция, удовлетворяющая исходному уравнению, то задача решена, независимо от того, какими соображениями мы пользовались при выборе этой функции.

При доказательстве неинтегрируемости некоторой функции в классе элементарных функций, наоборот, трансцендентность и возможный вид зависимости играет решающую роль.

23.15. ПРИМЕР. Рассмотрим уравнение

$\begin{equation} g'(x)=e^{-x^2}. \end{equation}$

( 23.2)

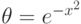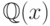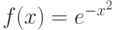Введем обозначение $\theta =e^{-x^2}$ . Тогда элемент $\theta$ трансцендентен над $\mathbb Q (x)$ (даже над $\mathbb C(x)$ ) и $\theta '=-2x\theta$ . Функция $f(x)=e^{-x^2}$ лежит в дифференциальном поле $\mathbb Q (x,\theta )$ .

Дальше >>

Введение в компьютерную алгебру

Введение в компьютерную алгебру

Интегрирование полиномов и рациональных функций. Некоторые сведения из дифференциальной алгебры. Структурная теорема

Вопросы и ответы

Студенты

Авторизоваться

Введение в компьютерную алгебру

Введение в компьютерную алгебру

Интегрирование полиномов и рациональных функций. Некоторые сведения из дифференциальной алгебры. Структурная теорема

Вопросы и ответы

Студенты