Обработка данных
Матричный метод анализа сетей Петри
Матричный метод основан на выражении (8.5), связывающим разметки сети, которые были до и после срабатывания некоторого перехода и матрице  , описывающей работу сети.
, описывающей работу сети.
Пусть начальная разметка сети равна 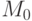 . Если в сети допустима последовательность срабатывания переходов
. Если в сети допустима последовательность срабатывания переходов 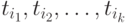 , то выполняются следующие соотношения
, то выполняются следующие соотношения
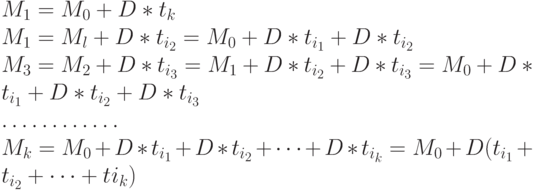
Обозначив 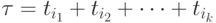 ,получим
,получим
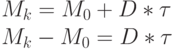 |
( 8.7) |
Из-за того, что вектор тявляется суммой векторов вида (8.2) он должен быть целочисленным неотрицательным вектором. Выполнение соотношения (8.6) для некоторого целочисленного неотрицательного вектора  является необходимым условием достижимости разметки
является необходимым условием достижимости разметки 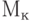 из началь-ной разметки
из началь-ной разметки 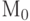 .
.
Выражение (8.7) является системой линейных неоднородных уравнений относительно неизвестных компонент вектора  . Следует заметить, что целочисленное неотрицательное решение уравнения (8.7), как правило, не определяет однозначно порядок срабатывания переходов, потому что от порядка суммирования векторов
. Следует заметить, что целочисленное неотрицательное решение уравнения (8.7), как правило, не определяет однозначно порядок срабатывания переходов, потому что от порядка суммирования векторов 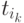 вида (8.2) сумма
вида (8.2) сумма 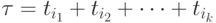 не зависит. Для нахождения требуемого порядка срабатывания переходов необходимо проводить дополнительные исследования.
не зависит. Для нахождения требуемого порядка срабатывания переходов необходимо проводить дополнительные исследования.
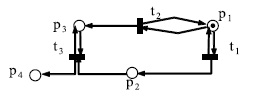
Рассмотрим пример решения матричным методом задачи о достижимости. Спрашивается, достижима ли разметка 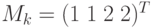 для сети Петри, изображенной на рис.8.9?
для сети Петри, изображенной на рис.8.9?
Если разметка достижима, то указать последовательность срабатываний переходов, приводящую к данной разметке.
Матрица  для данной сети Петри имеет вид
для данной сети Петри имеет вид
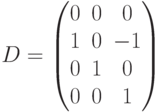
Матричное уравнение (8.6) для определения последовательности срабатываний переходов имеет вид
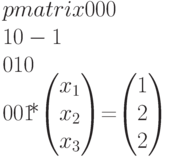
Без первого уравнения, которое тривиально выполняется, имеем систему трех уравнений с тремя неизвестными
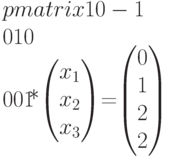
Из второго и третьего уравнений получаем 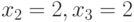 , а из первого
, а из первого 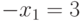 . Таким образом, в качестве решения имеем целочисленный неотрицательный вектор
. Таким образом, в качестве решения имеем целочисленный неотрицательный вектор
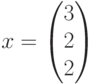
Этот вектор не определяет порядок срабатывания переходов. Среди последовательностей срабатывания есть невыполнимые, например, 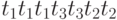 . Среди последовательностей срабатывания переходов, удовлетворяющих вектору, необходимо искать допустимые. Допустимых после-довательностей может быть много, а может и не быть вовсе. Для данного примера допустимой последовательностью является последовательность
. Среди последовательностей срабатывания переходов, удовлетворяющих вектору, необходимо искать допустимые. Допустимых после-довательностей может быть много, а может и не быть вовсе. Для данного примера допустимой последовательностью является последовательность 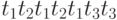 или последовательность
или последовательность 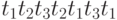 .
.
Наличие неотрицательного положительного решения у линейного уравнения для определения последовательности срабатывания является только необходимым условием и не гарантирует реального существова-ния такой последовательности. Например, решая задачу о достижимости разметки 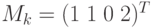 для описанной выше сети Петри, в качестве решения мы получим неотрицательный целочисленный вектор
для описанной выше сети Петри, в качестве решения мы получим неотрицательный целочисленный вектор

Однако реальной последовательности, приводящей к требуемой разметке, не существует, так как для срабатывания перехода 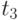 необходимо наличие в месте
необходимо наличие в месте 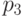 маркера. Но фишка, попавшая в
маркера. Но фишка, попавшая в 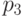 , не может покинуть эту позицию.
, не может покинуть эту позицию.
Пример 2 (решение матричным методом задачи о достижимости).
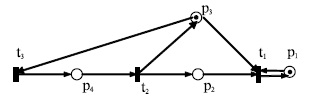
Рассмотрим сеть
и исследуем достижимость разметки 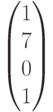 из начальной разметки
из начальной разметки 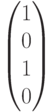
Матрица  имеет вид
имеет вид
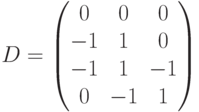
Матричное уравнение для определения последовательности срабатываний переходов имеет вид
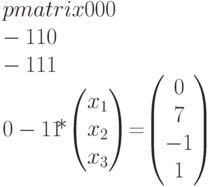
Без первого уравнения, которое тривиально выполняется, имеем систему
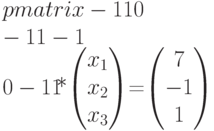
Складывая второе и третье уравнения, получим  . Из первого уравнения получаем
. Из первого уравнения получаем 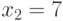 , а из третьего -
, а из третьего -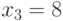 . Таким образом, в качестве решения имеем целочисленный неотрицательный вектор
. Таким образом, в качестве решения имеем целочисленный неотрицательный вектор
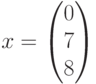
Этот вектор не определяет порядок срабатывания переходов. Среди последовательностей срабатывания есть невыполнимые, например

Среди последовательностей срабатывания переходов, удовлетворяющих вектору, необходимо искать допустимые. Допустимых последовательностей может быть много, а может и не быть вовсе. Для данного примера допустимой последовательностью является последовательность 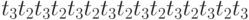 .
.
Матричный подход может быть использован для вектора весов, относительно которого сеть Петри является сохраняющей (консервативной). Пусть 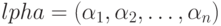 - вектор-строка искомых весов. В соответствии с приведенным выше определением консервативность сети заключается в выполнении равенства (8.6). Обе части этого равенства можно рассматривать как скалярные произведения вектора
- вектор-строка искомых весов. В соответствии с приведенным выше определением консервативность сети заключается в выполнении равенства (8.6). Обе части этого равенства можно рассматривать как скалярные произведения вектора  на векторы любых двух достижимых разметок. Если в качестве одной из разметок взять начальную разметку
на векторы любых двух достижимых разметок. Если в качестве одной из разметок взять начальную разметку 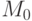 , а в качестве второй - любую достижимую разметку, то из (8.6) следует, что
, а в качестве второй - любую достижимую разметку, то из (8.6) следует, что  . Из формулы (8.5) следует, что
. Из формулы (8.5) следует, что 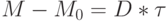 . В результате получаем, что
. В результате получаем, что  для всех векторов
для всех векторов  , соответствующих достижимым разметкам. Равенство выполняется, если
, соответствующих достижимым разметкам. Равенство выполняется, если 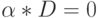 . Это матричное выражение представляет собой линейное однородное уравнение относительно весов, составляющих вектор
. Это матричное выражение представляет собой линейное однородное уравнение относительно весов, составляющих вектор 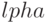 .
.
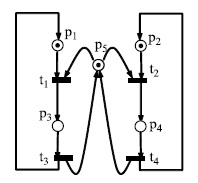
Для сети, изображенной на рис.8.10, найдем матричным методом вектор весов  , относительно которого она является сохраняющей. Эта сеть моделирует два взаимодействующих процесса обработки, использующих общий ресурс (описывается местом
, относительно которого она является сохраняющей. Эта сеть моделирует два взаимодействующих процесса обработки, использующих общий ресурс (описывается местом 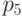 ).
).
Матрица  для данной сети имеет вид
для данной сети имеет вид
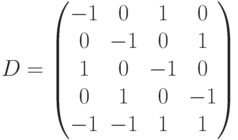
Легко заметить, что эта матрица имеет ранг 2 (третий столбец равен первому, умноженному на -1, а четвертый столбец равен второму, умноженному на -1). Поэтому система уравнений 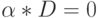 для вектора весов
для вектора весов 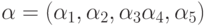 включает в себя только два уравнения
включает в себя только два уравнения
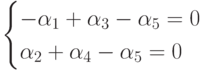
Существует бесконечно много решений этой системы, которые могут быть получены из выражений
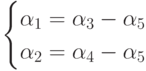
при произвольном задании весов 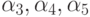 . Из этих выражений видно, что сеть не является строго сохраняющей, т. к. вектор (1, 1, 1, 1, 1) не является решением системы. В качестве вектора весов, относительно которого сеть является сохраняющей, нас интересуют только неотрицательные решения. Задавая
. Из этих выражений видно, что сеть не является строго сохраняющей, т. к. вектор (1, 1, 1, 1, 1) не является решением системы. В качестве вектора весов, относительно которого сеть является сохраняющей, нас интересуют только неотрицательные решения. Задавая 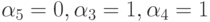 , , получим
, , получим 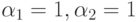 . Вектор весов (1, 1, 1, 1, 0), являющийся решением системы, означает, что сеть сохраняет суммарное количество фишек во всех местах, за исключением места
. Вектор весов (1, 1, 1, 1, 0), являющийся решением системы, означает, что сеть сохраняет суммарное количество фишек во всех местах, за исключением места 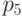 (количество фишек в месте
(количество фишек в месте 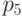 не учитывается при подсчете обще-го числа в сети). Еще одно решение (1, 1, 2, 2, 1) соответствует случаю, когда фишки в местах
не учитывается при подсчете обще-го числа в сети). Еще одно решение (1, 1, 2, 2, 1) соответствует случаю, когда фишки в местах 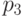 и
и 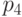 учитываются при подсчете взвешенной суммы фишек в сети с коэффициентом 2.
учитываются при подсчете взвешенной суммы фишек в сети с коэффициентом 2.