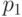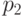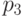Обработка данных
Формальное определение сети Петри
Чтобы можно было использовать сети Петри для анализа процессов обработки, необходимо иметь точное определение.
Графом сети Петри будем называть тройку (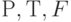 ), где
), где
 - непустое множество элементов сети, называемых местами,
- непустое множество элементов сети, называемых местами,
 - непустое множество элементов сети, называемых переходами,
- непустое множество элементов сети, называемых переходами,
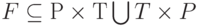 - отношение инцидентности,
- отношение инцидентности,
и для (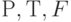 ) выполнены следующие условия:
) выполнены следующие условия:
-
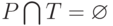 (множества мест и переходов не пересекаются);
(множества мест и переходов не пересекаются); -
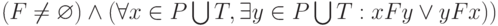 (т.е. любой элемент сети инцидентен хотя бы одному элементу другого типа);
(т.е. любой элемент сети инцидентен хотя бы одному элементу другого типа); -
если для произвольного элемента сети
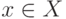 обозначить через
обозначить через 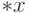 множество его входных элементов
множество его входных элементов 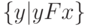 , а через
, а через  - множество его выходных элементов
- множество его выходных элементов 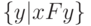 , то
, то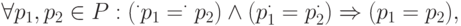
то есть сеть не содержит пары мест, которые инцидентны одному и тому же множеству переходов.
Графическим представлением сети служит двудольный ориентированный граф с двумя типами вершин; вершины-места изображаются кружочками, вершины-переходы - барьерами. Из вершины  в вершину
в вершину  ведет дуга, если и только если
ведет дуга, если и только если 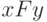 .
.
На основе понятия сети, которая описывает только статическую топологию моделируемого процесса или системы, вводятся динамические сетевые структуры, в которых местам приписываются специальные разметки, моделирующие выполнение условия, и с сетью связывается понятие ее функционирования, изменяющего эти разметки (условия) в результате так называемых срабатываний переходов. К таким динамическим сетям относятся сети Петри, их различные варианты, обобщения и частные случаи.
Сеть Петри - это набор  , где
, где 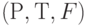 - конечная сеть (множество
- конечная сеть (множество 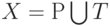 конечно), a
конечно), a 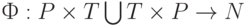 и
и 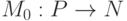 - две функции, называемые соответственно кратностью дуг и начальной разметкой. Первая сопоставляет каждой дуге число
- две функции, называемые соответственно кратностью дуг и начальной разметкой. Первая сопоставляет каждой дуге число  (кратность дуги). Если
(кратность дуги). Если  , то в графическом представлении сети число
, то в графическом представлении сети число  выписывается рядом с короткой чертой, пересекающей дугу. Часто такая дуга будет также заменяться пучком из
выписывается рядом с короткой чертой, пересекающей дугу. Часто такая дуга будет также заменяться пучком из  дуг, соединяющих соответствующие элементы сети. Условимся никак не отмечать кратность дуг, равную 1. Такую сеть будем называть ординарной. Вторая функция сопоставляет каждому месту
дуг, соединяющих соответствующие элементы сети. Условимся никак не отмечать кратность дуг, равную 1. Такую сеть будем называть ординарной. Вторая функция сопоставляет каждому месту 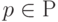 некоторое число
некоторое число 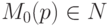 (разметка места). В графическом представлении сети разметка места
(разметка места). В графическом представлении сети разметка места  изображается помещением в вершину-кружок числа
изображается помещением в вершину-кружок числа 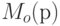 или, если это число невелико, соответствующего числа точек (фишек).
или, если это число невелико, соответствующего числа точек (фишек).
Разметка сети  - это функция
- это функция 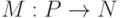 . Если предположить, что все места сети
. Если предположить, что все места сети  строго упорядочены каким-либо образом, т.е.
строго упорядочены каким-либо образом, т.е. 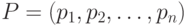 , то разметку
, то разметку  сети (в том числе начальную разметку) можно задать как вектор целых неотрицательных чисел
сети (в том числе начальную разметку) можно задать как вектор целых неотрицательных чисел
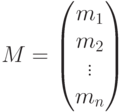
такой, что для любого 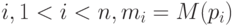 .
.
На основе отношения инцидентности  можно ввести функцию инцидентности
можно ввести функцию инцидентности 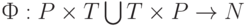 , которая определяется выражением
, которая определяется выражением
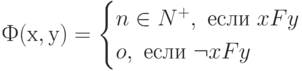
Значения функции 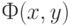 можно трактовать как кратность дуги между вершинами сети
можно трактовать как кратность дуги между вершинами сети  и
и  . Если
. Если 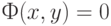 , то это означает, что между вершинами
, то это означает, что между вершинами  и
и  дуги нет.
дуги нет.
Если места сети упорядочены, то можно каждому переходу  сопоставить два целочисленных вектора
сопоставить два целочисленных вектора 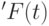 и
и 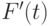 длиной
длиной  , где
, где 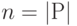 :
:
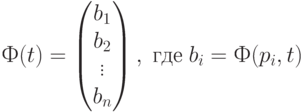
и
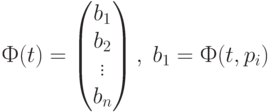
Функционирование сети Петри описывается формально с помощью множества последовательностей срабатываний и множества достижимых в сети разметок. Эти понятия определяются через правила срабатывания переходов сети.
Переход  может сработать при некоторой разметке
может сработать при некоторой разметке  сети
сети  , если
, если 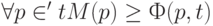 , то есть каждое входное место
, то есть каждое входное место  перехода
перехода  имеет разметку, не меньшую, чем кратность дуги, соединяющей
имеет разметку, не меньшую, чем кратность дуги, соединяющей  и
и  . Это условие можно переписать в векторной форме следующим образом:
. Это условие можно переписать в векторной форме следующим образом: 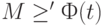 .
.
Предполагается, что для векторов 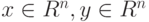 выражение
выражение  озна-чает, что
озна-чает, что 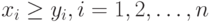 .
.
Из определения векторов 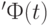 и
и 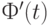 ясно, что вектор
ясно, что вектор 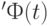 является столбцом матрицы
является столбцом матрицы 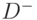 , а вектор
, а вектор 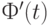 является столбцом матрицы
является столбцом матрицы 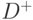
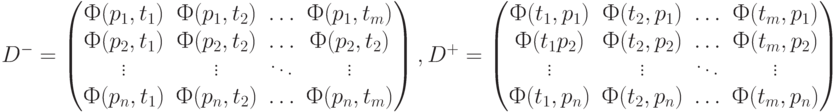
Векторы 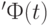 и
и 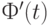 могут быть представлены как произведения
могут быть представлены как произведения  и
и  матриц
матриц 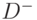 и
и 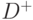 на вектор
на вектор 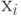 вида
вида
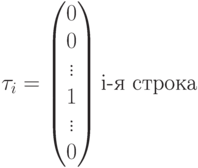 |
( 8.3) |
у которого все компоненты равны 0, кроме 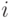 -й компоненты, равной 1.
-й компоненты, равной 1.
Для ординарной сети Петри условие срабатывания перехода означает, что любое входное место этого перехода содержит хотя бы одну фишку, т.е. имеет ненулевую разметку.
Срабатывание перехода 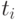 при разметке
при разметке 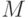 порождает разметку
порождает разметку 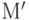 по следующему правилу:
по следующему правилу:
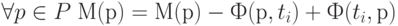
В матричном виде изменение разметки при срабатывании перехода 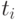 описывается выражением
описывается выражением
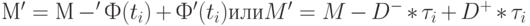 |
( 8.4) |
Обозначив 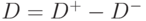 , получим еще более краткую запись для выражения (8.4)
, получим еще более краткую запись для выражения (8.4)
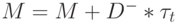 |
( 8.5) |
Таким образом, срабатывание перехода  изменяет разметку так, что разметка каждого его входного места
изменяет разметку так, что разметка каждого его входного места  уменьшается на
уменьшается на 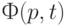 , т.е. на кратность дуги, соединяющей
, т.е. на кратность дуги, соединяющей  и
и  , а разметка каждого его выходного места увеличивается на
, а разметка каждого его выходного места увеличивается на 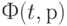 , т.е. на кратность дуги, соединяющей
, т.е. на кратность дуги, соединяющей  и
и  .
.
Элемент матрицы 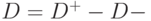 , находящийся в
, находящийся в  -й строке и
-й строке и  -м столбце, представляет собой разность числа появившихся и удаленных в
-м столбце, представляет собой разность числа появившихся и удаленных в  -м месте фишек в результате срабатывания
-м месте фишек в результате срабатывания  -го перехода.
-го перехода.
На множестве разметок можно ввести отношение непосредственного следования разметок:
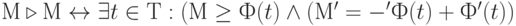
Будем использовать уточняющее обозначение 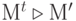 , если
, если 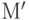 непосредственно следует после
непосредственно следует после  в результате срабатывания перехода
в результате срабатывания перехода 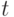 .
Говорят, что разметка
.
Говорят, что разметка 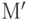 достижима от разметки
достижима от разметки  , если существует последовательность разметок
, если существует последовательность разметок 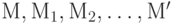 и слово
и слово 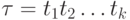 в алфавите
в алфавите  , такие что
, такие что
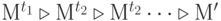
Слово  в этом случае называется последовательностью срабатываний, ведущих от
в этом случае называется последовательностью срабатываний, ведущих от  к
к 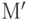 . Обобщим отношения непосредственного следования до отношения "
. Обобщим отношения непосредственного следования до отношения "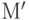 достижима от
достижима от  ", используя обозначение
", используя обозначение 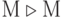 или
или 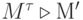 , если уточняется последовательность срабатываний (последовательность может быть пустой, т.е.
, если уточняется последовательность срабатываний (последовательность может быть пустой, т.е. 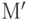 не достижима от
не достижима от  ).
).
Множество 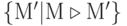 разметок, достижимых в сети
разметок, достижимых в сети  от разметки
от разметки  , обозначим через
, обозначим через 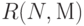 . Множество
. Множество 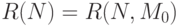 , т.е. множество всех разметок, достижимых в
, т.е. множество всех разметок, достижимых в  от начальной разметки
от начальной разметки 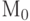 , называют множеством достижимых разметок сети
, называют множеством достижимых разметок сети  (заметим, что
(заметим, что 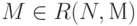 и
и  ).
).
Множеством последовательностей срабатываний сети  , или свободным языком сети
, или свободным языком сети  , называется множество
, называется множество
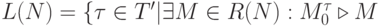
то есть множество всех последовательностей срабатываний, ведущих от 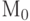 к каждой достижимой в
к каждой достижимой в  разметке.
разметке.
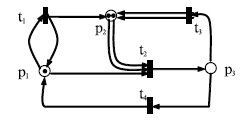
На рис.8.6 изображена сеть Петри, на примере которой поясним данные выше определения. В этой сети 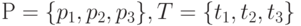 . Функция инцидентности
. Функция инцидентности  задается с помощью следующих двух таблиц, в которых на пересечении строки
задается с помощью следующих двух таблиц, в которых на пересечении строки  и столбца
и столбца  стоит число
стоит число 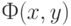 :
:
Начальная разметка 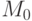 задается следующим образом:
задается следующим образом: 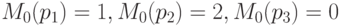 , или в векторной форме:
, или в векторной форме: 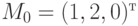 .
.
При разметке 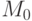 могут сработать переходы
могут сработать переходы 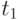 и
и 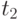 , так как
, так как  . Переходы
. Переходы 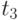 и
и 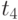 не могут сработать, так как вектор начальной разметки
не могут сработать, так как вектор начальной разметки 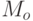 не покрывает векторы
не покрывает векторы 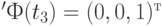 , и
, и  .
.
В результате срабатывания перехода 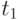 разметка
разметка 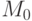 сменяется на разметку (1, 3, 0), а в результате срабатывания перехода
сменяется на разметку (1, 3, 0), а в результате срабатывания перехода 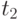 разметка
разметка 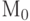 сменяется на разметку (0, 0, 1) . Обе новые разметки непосредственно следуют после
сменяется на разметку (0, 0, 1) . Обе новые разметки непосредственно следуют после 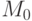 в рассматриваемой сети. Можно представить возможные изменения разметок сети
в рассматриваемой сети. Можно представить возможные изменения разметок сети  , происходящие в результате срабатывания ее переходов, в виде графа разметок - ориентированного графа, множество вершин которого образовано множеством
, происходящие в результате срабатывания ее переходов, в виде графа разметок - ориентированного графа, множество вершин которого образовано множеством 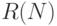 достижимых в
достижимых в  разметок. Из вершины
разметок. Из вершины  в вершину
в вершину 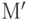 ведетa дуга, помеченная символом перехода
ведетa дуга, помеченная символом перехода  , если и только если
, если и только если 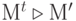 . На рис.8.7 показан начальный фрагмент графа разметок сети на рис.8.6. Этот граф бесконечен, так как множество
. На рис.8.7 показан начальный фрагмент графа разметок сети на рис.8.6. Этот граф бесконечен, так как множество 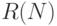 достижимых разметок бесконечно для рассматриваемой сети.
достижимых разметок бесконечно для рассматриваемой сети.
Разметка  называется тупиковой, если в сети
называется тупиковой, если в сети  не существует ни одного перехода, который может сработать при этой разметке. Для рассматриваемой сети тупиковыми являются разметки (0, 2, 0), (0, 3, 0), (0,4,0),..., (0, n, 0)...
не существует ни одного перехода, который может сработать при этой разметке. Для рассматриваемой сети тупиковыми являются разметки (0, 2, 0), (0, 3, 0), (0,4,0),..., (0, n, 0)...
Легко видеть, что если выделить путь по дугам графа разметок, начинающийся в вершине  и заканчивающийся в вершине
и заканчивающийся в вершине 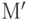 , и выписать подряд все встречающиеся символы переходов, то полученное слово образует последовательность срабатываний, ведущих от
, и выписать подряд все встречающиеся символы переходов, то полученное слово образует последовательность срабатываний, ведущих от  к
к 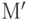 . Множество всех слов, которые получены выписыванием символов переходов вдоль путей, начинающихся в
. Множество всех слов, которые получены выписыванием символов переходов вдоль путей, начинающихся в 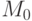 , образует множество последовательностей срабатываний сети, или ее свободный язык. Так, язык рассматриваемой сети включает слова
, образует множество последовательностей срабатываний сети, или ее свободный язык. Так, язык рассматриваемой сети включает слова 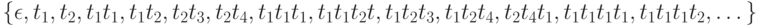 .
.