| Что такое сеть? |
Графы с цветными ребрами
Установлено свойство графа, являющееся обобщением свойства 2.
Свойство 4. В любом полном графе с шестью или более вершинами и ребрами одного из двух цветов всегда найдутся два разных треугольника с одноцветными сторонами. Эти два треугольника могут иметь общую вершину или даже общее ребро.
Если два треугольника имеют общую вершину или ребро, то их называют сцепленными.
Рассмотрим свойства полного графа, ребра которого окрашены в один из трех цветов, каждый цвет соответствует одному из трех отношений между объектами заданного множества.
Задача 4. Каждый из семнадцати ученых переписывается с остальными. В их переписке речь идет лишь о трех темах. Каждая пара ученых переписывается друг с другом лишь по одной теме. Нужно доказать, что не менее трех ученых переписываются друг с другом по одной и той же теме.
Решение. Условию задачи соответствует полный граф с семнадцатью
вершинами и ребрами трех цветов. Из каждой вершины выходит шестнадцать
ребер. Докажем, что в таком графе найдется хотя бы один треугольник с
одноцветными сторонами. Заметим, что каждая вершина этого графа
принадлежит хотя бы шести ребрам одного цвета. Пусть, например, вершина  принадлежит шести красным ребрам.
принадлежит шести красным ребрам.
Если среди вершин  найдутся две, которые соединены красным ребром, то получится треугольник с красными
сторонами. Если не найдутся, то все шесть вершин
найдутся две, которые соединены красным ребром, то получится треугольник с красными
сторонами. Если не найдутся, то все шесть вершин 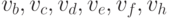 соединены между собой попарно ребрами двух цветов
(зеленым и синим). Как было доказано ранее, в этом графе с шестью
вершинами найдется хотя бы один треугольник либо с синими, либо с зелеными
сторонами. Задача решена.
соединены между собой попарно ребрами двух цветов
(зеленым и синим). Как было доказано ранее, в этом графе с шестью
вершинами найдется хотя бы один треугольник либо с синими, либо с зелеными
сторонами. Задача решена.
Сформулируем теперь свойство, доказанное при решении этой задачи.
Свойство 5. В полном графе с семнадцатью или более вершинами и ребрами трех цветов всегда найдется, по меньшей мере, один треугольник с одноцветными сторонами.
Заметим, что не случайно отношения, которые были найдены при решении
задач, изображавшиеся цветными ребрами, симметричны, если  — друг
— друг  , то
, то  —
друг
—
друг  , но не обязательно
транзитивны, если
, но не обязательно
транзитивны, если  — друг
— друг  и
и  —
друг
—
друг 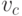 , то
, то  может и не быть
другом
может и не быть
другом 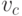 . В случае, когда
отношение между объектами было транзитивным, соответствующие
ребра образовывали треугольник с одноцветными сторонами.
. В случае, когда
отношение между объектами было транзитивным, соответствующие
ребра образовывали треугольник с одноцветными сторонами.
Задача 5. В работе
международного симпозиума лингвистов участвуют  человек. Из любых четырех один может объясняться с остальными тремя
хотя бы на одном языке. Нужно доказать, что найдется участник симпозиума,
который может объясниться с каждым из остальных участников.
человек. Из любых четырех один может объясняться с остальными тремя
хотя бы на одном языке. Нужно доказать, что найдется участник симпозиума,
который может объясниться с каждым из остальных участников.
Решение. Имеем полный граф
с  вершинами и ребрами двух
цветов (синее ребро — двое могут объясниться на каком-нибудь языке,
красное — не могут). По условию, среди любых четырех вершин графа всегда
найдется, по меньшей мере, одна, синяя степень которой равна трем.
вершинами и ребрами двух
цветов (синее ребро — двое могут объясниться на каком-нибудь языке,
красное — не могут). По условию, среди любых четырех вершин графа всегда
найдется, по меньшей мере, одна, синяя степень которой равна трем.
Случай, когда все ребра синие, тривиален, математически неинтересен. Пусть
найдется красное ребро 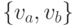 . Добавим еще какие-нибудь
две вершины
. Добавим еще какие-нибудь
две вершины 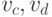 . Из четырех вершин
. Из четырех вершин 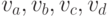 найдется хотя бы одна синяя,
степень которой равна трем. Это
найдется хотя бы одна синяя,
степень которой равна трем. Это 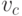 или
или 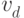 .
Пусть, например, синюю степень три имеет
.
Пусть, например, синюю степень три имеет 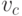 . Добавим еще
одну вершину —
. Добавим еще
одну вершину — 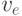 . Из вершин
. Из вершин 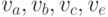 или
или 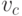 или
или 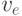 имеет синюю степень, равную
трем. В обоих случаях
имеет синюю степень, равную
трем. В обоих случаях 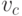 соединена синим ребром
с
соединена синим ребром
с 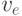 .
Переберем все вершины. В итоге окажется, что
.
Переберем все вершины. В итоге окажется, что 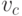 соединена
синим ребром со всеми вершинами графа. Во всякой четверке вершин,
включая
соединена
синим ребром со всеми вершинами графа. Во всякой четверке вершин,
включая  и
и  , есть вершина, соединенная синим ребром со всеми
остальными вершинами графа. Отсюда, кроме
, есть вершина, соединенная синим ребром со всеми
остальными вершинами графа. Отсюда, кроме  и
и  , существует самое большее одна вершина, не соединенная синим ребром
со всеми остальными.
, существует самое большее одна вершина, не соединенная синим ребром
со всеми остальными.

