Графы с цветными ребрами

Кроме того, при ее решении доказаны два свойства таких графов.

Свойство 1. Любая вершина полного графа с шестью или более вершинами и ребрами двух цветов принадлежит, по меньшей мере, трем ребрам одного цвета.

Свойство 2. В любом полном графе с шестью или более вершинами и ребрами двух цветов найдется, по меньшей мере, один треугольник с одноцветными сторонами.

Задача 2. На географической карте выбраны пять городов. Известно, что среди них из любых трех найдутся два, соединенные авиалиниями, и два — несоединенные. Требуется доказать, что:

1. Каждый город соединен авиалиниями непосредственно с двумя и только с двумя другими городами.
2. Вылетев из любого города, можно облететь остальные, побывав в каждом по одному разу, и вернуться назад.

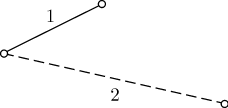
Решение. Рассматривается множество объектов — городов и два отношения, заданные для элементов этого множества. Каждые два города находятся в одном из двух отношений — они либо соединены между собой авиалиниями, либо не соединены. Пусть вершины графа соответствуют городам: красное ребро (пронумеровано 1) соответствует наличию авиалиний, синее ребро (пронумеровано 2) соответствует отсутствию авиалиний. По условию среди трех ребер, соединяющих любые три вершины, одно — красное, второе — синее,

а это означает, что в графе нет ни одного треугольника с одноцветными сторонами. Тогда из решения предыдущей задачи следует, что каждая вершина непременно принадлежит двум красным ребрам и двум синим,

поскольку в противном случае образовался бы треугольник с одноцветными сторонами. А это и означает, что каждый город соединен авиалиниями с двумя и только с двумя городами.

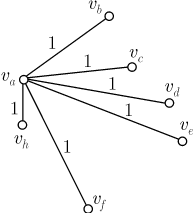
Остается показать, что в графе найдется "пятиугольник", все ребра которого — красные.

Выберем одну из вершин, например , а красными будут, скажем, ребра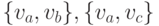

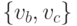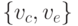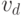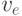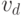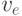Ребро не может быть красным, следовательно, красным является одно из ребер: либо , либо . Пусть красное . Если теперь соединить красным ребром вершины и , то вершина должна быть соединена красными ребрами с вершинами, которые принадлежат уже двум красным ребрам. По условию это невозможно. Остается соединить красными ребрами вершины и , и 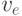. Остальные ребра должны быть синими.

Итак, мы получили еще одно свойство.

Свойство 3. Если в полном графе с пятью вершинами и ребрами двух цветов не найдется треугольника с одноцветными сторонами, то граф можно изобразить в виде "пятиугольника" с красными сторонами и синими диагоналями.

В формулировке свойства 3 можно заменить слово "красный" на "синий" и одновременно слово "синий" на "красный", то есть речь пойдет о пятиугольнике с синими сторонами и красными диагоналями. Это понятно, поскольку для пятиугольника и только для него характерно, что его диагонали образуют также пятиугольник.

Задача 3. В течение дня двое из шести телефонных абонентов могут поговорить друг с другом по телефону, а могут и не поговорить. Докажем, что всегда можно указать две тройки абонентов, в каждой из которых все переговорили друг с другом или все не переговорили.

Решение. Пусть у полного графа с шестью вершинами красные ребра соответствуют парам абонентов, которые говорили друг с другом по телефону, синие — тем, кто не говорил. Тогда в графе найдется хотя бы один треугольник, 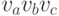, с одноцветными сторонами.

Остается показать, что обязательно найдется еще и второй такой треугольник.

Временно исключим из рассмотрения одну из его вершин, скажем , вместе с ребрами, принадлежащим ей.

Найдется ли в оставшемся графе с пятью вершинами треугольник с одноцветными сторонами? Если найдется, то он содержится и в исходном графе.

В противном случае получается пятиугольник с красными сторонами и синими диагоналями. Теперь восстановим шестую вершину с ее ребрами.

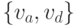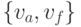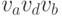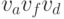Если ребро или ребро будет окрашено в красный цвет, то образуется еще минимум один треугольник с красными сторонами или . Если оба эти ребра будут синего цвета, то появится треугольник с синими сторонами. Вывод нетрудно перевести с языка теории графов на язык задачи.