| Что такое сеть? |
Эйлеровы графы
Решение задачи о лабиринтах
Правило 1. Отправляемся от выбранной вершины (первого перекрестка) и идем по любому ребру, пока не приходим или в тупик (к вершине), или к новому перекрестку (вершине).
Тогда:
- Если окажется, что мы попали в тупик, возвращаемся назад и пройденное ребро должно быть уже отброшено, так как мы прошли его два раза (туда и обратно).
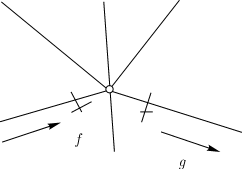
- Если приходим к новому перекрестку, то направляемся по новому произвольному ребру, не забывая всякий раз отмечать путь, по которому прибыли, и путь, по которому отправились дальше. Как показано на рисунке.
Пример.
Направление движения показано стрелкой  . После прихода к
пересечению путей выбирается направление, обозначенное стрелкой
. После прихода к
пересечению путей выбирается направление, обозначенное стрелкой  . Оба пути
помечаются черточкой. (Крестиками обозначаются черточки, поставленные при
последнем прохождении через перекресток.)
. Оба пути
помечаются черточкой. (Крестиками обозначаются черточки, поставленные при
последнем прохождении через перекресток.)
Следуем указанному выше первому правилу всякий раз, когда приходим на такой перекресток, на котором еще не были. В конце концов мы должны прийти к перекрестку, на котором уже были, и здесь может представиться два случая. По какому пути пришли: по дороге, раз пройденной, или по новому пути.
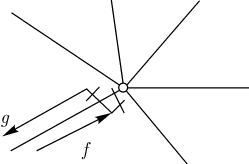
Правило 2. Прибыв на известный нам перекресток по новой дороге, мы должны сейчас же повернуть обратно, предварительно отметив этот путь двумя черточками (прибытие и обратное отправление), как показано на рисунке.
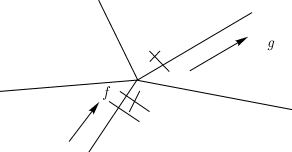
Правило 3. Если мы приходим на известный перекресток таким путем, которым уже раз прошли, то, отметив этот путь второй черточкой, отправляемся дальше путем, которым еще не проходили, если только такой путь существует. Этот случай изображен на рисунке.
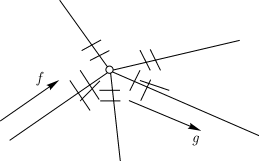
Но если такого пути нет, то выбирается дорога, по которой мы прошли только один раз. Случай этот показан на рисунке.
Придерживаясь указанных правил, обойдем два раза все линии сети и придем в точку отправления. Это можно доказать, сделав предварительно такие замечания:
- Выходя из точки отправления
 , ставим начальный знак
(поперечную черточку).
, ставим начальный знак
(поперечную черточку). - Прохождение через перекресток по одному из предыдущих трех правил каждый раз добавляет два знака (две поперечные черточки) на линиях, которые сходятся в этой точке.
- В любой момент прохождения лабиринта, перед прибытием на какой-либо перекресток или после отправления из него, начальный перекресток (пункт отправления) имеет нечетное число знаков (черточек), а всякий другой перекресток имеет их четное число.
- В любой момент, до или после прохода через перекресток, начальный перекресток имеет только один путь, обозначенный только одной черточкой. Любой другой из посещенных уже перекрестков может иметь только два пути, обозначенных одной черточкой.
- После полного обхода лабиринта у всех перекрестков все пути должны иметь по две черточки. Это, впрочем, входит в условие задания.
Приняв во внимание все вышеизложенное, убеждаемся, что если кто-либо
отправляется из начального перекрестка, скажем  , и прибывает
в какой-либо иной перекресток
, и прибывает
в какой-либо иной перекресток 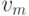 , то он не может встретить
таких трудностей задачи, которые могли бы остановить его дальнейшее путешествие.
В самом деле, в это место он приходит или новым путем, или путем, который
уже один раз пройден. В первом случае прилагается первое или второе из
приведенных выше правил. Во втором случае вход на перекресток
, то он не может встретить
таких трудностей задачи, которые могли бы остановить его дальнейшее путешествие.
В самом деле, в это место он приходит или новым путем, или путем, который
уже один раз пройден. В первом случае прилагается первое или второе из
приведенных выше правил. Во втором случае вход на перекресток 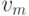 и остановка здесь дала бы нечетное число знаков около него,
следовательно, за неимением нового пути надо пойти по уже пройденному один
раз пути, и около перекрестка будет четное число знаков (если он не
начальный) по замечанию 3.
и остановка здесь дала бы нечетное число знаков около него,
следовательно, за неимением нового пути надо пойти по уже пройденному один
раз пути, и около перекрестка будет четное число знаков (если он не
начальный) по замечанию 3.
Пусть, наконец, мы будем вынуждены закончить путь и вернуться в начальный
перекресток  . Обозначим это ребро
. Обозначим это ребро  , то есть оно ведет из перекрестка
, то есть оно ведет из перекрестка 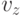 в начальный
в начальный  .
Этот путь должен быть тем самым, которым мы отправлялись первый раз из
.
Этот путь должен быть тем самым, которым мы отправлялись первый раз из  , иначе путь можно было бы продолжать. И если теперь мы принуждены этим же
путем возвратиться в начальную точку (вершину), то это значит, что из
перекрестка
, иначе путь можно было бы продолжать. И если теперь мы принуждены этим же
путем возвратиться в начальную точку (вершину), то это значит, что из
перекрестка 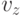 нет никакого другого пути, который бы не был уже
два раза пройден. Иначе это означало бы, что забыли применить первую часть
правила
нет никакого другого пути, который бы не был уже
два раза пройден. Иначе это означало бы, что забыли применить первую часть
правила  , более того, это означало бы, что в
, более того, это означало бы, что в 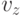 есть какой-то путь
есть какой-то путь  , пройденный только один раз по
замечанию
, пройденный только один раз по
замечанию  . Итак, при последнем возвращении в
. Итак, при последнем возвращении в  все пути в
все пути в 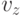 должны быть отмечены двумя черточками. Точно так же это можно доказать для
предыдущего перекрестка
должны быть отмечены двумя черточками. Точно так же это можно доказать для
предыдущего перекрестка 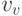 , и для всех остальных. Другими
словами, предположение доказано, и задача решена.
, и для всех остальных. Другими
словами, предположение доказано, и задача решена.