| Что такое сеть? |
Эйлеровы графы
Теорема 4.3.
Если граф  обладает эйлеровым путем
с концами
обладает эйлеровым путем
с концами  и
и 
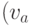 не
совпадает с
не
совпадает с 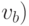 ,
то граф
,
то граф  является связным, и
является связным, и  и
и  —
единственные нечетные его вершины.
—
единственные нечетные его вершины.
Доказательство
Связность графа следует из определения эйлерова пути. Если путь
начинается в  , а заканчивается в другой вершине
, а заканчивается в другой вершине  , то
, то  и
и  —
нечетные, даже если путь неоднократно проходил через
—
нечетные, даже если путь неоднократно проходил через  и
и  .
В любую другую вершину графа путь должен был привести и вывести из нее,
то есть все остальные вершины должны быть четными.
.
В любую другую вершину графа путь должен был привести и вывести из нее,
то есть все остальные вершины должны быть четными.
Верно и обратное.
Теорема 4.4.
Если граф  связный и
связный и  и
и  единственные нечетные
вершины его, то граф
единственные нечетные
вершины его, то граф  обладает эйлеровым путем
с концами
обладает эйлеровым путем
с концами  и
и  .
.
Доказательство
Вершины  и
и  могут быть соединены ребрами в
графе.
могут быть соединены ребрами в
графе.
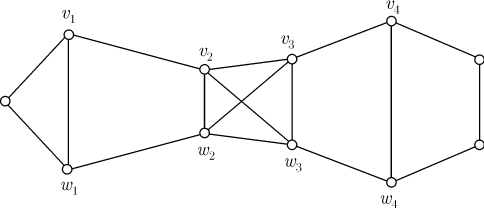
Пример.
А могут быть и не соединены.
Если  и
и  соединены ребром, то удалим
его. Тогда все вершины станут четными. Новый граф, согласно предыдущей
теореме, обладает эйлеровым циклом, началом и концом которого может
служить любая вершина. Начнем эйлеров путь в вершине
соединены ребром, то удалим
его. Тогда все вершины станут четными. Новый граф, согласно предыдущей
теореме, обладает эйлеровым циклом, началом и концом которого может
служить любая вершина. Начнем эйлеров путь в вершине  и закончим его в вершине
и закончим его в вершине  . Добавим ребро
(
. Добавим ребро
( 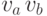 ) и получим эйлеров путь с началом в
) и получим эйлеров путь с началом в  и концом в
и концом в  .
.
Если  и
и  не соединены ребром, то к
графу добавим новое ребро (
не соединены ребром, то к
графу добавим новое ребро (  ,
,  ), тогда все
вершины его станут четными. Новый граф, согласно предыдущей теореме, обладает
эйлеровым циклом. Начнем его из вершины
), тогда все
вершины его станут четными. Новый граф, согласно предыдущей теореме, обладает
эйлеровым циклом. Начнем его из вершины  по ребру
(
по ребру
(  ,
,  ). Закончится путь тоже в вершине
). Закончится путь тоже в вершине  . Если теперь удалить из полученного цикла ребро
(
. Если теперь удалить из полученного цикла ребро
(  ,
,  ),
то останется эйлеров путь с началом в
),
то останется эйлеров путь с началом в  и концом в
и концом в  или с началом
в
или с началом
в  и концом в
и концом в  .
.
Таким образом, всякую замкнутую фигуру, имеющую в точности две нечетные вершины, можно начертить одним росчерком без повторений, начав в одной из нечетных вершин, а закончив в другой.
Теорема 4.5.
Если связный граф  имеет
имеет 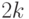 нечетных вершин, то
найдется
семейство из
нечетных вершин, то
найдется
семейство из  путей, которые в совокупности содержат все
ребра графа в точности по одному разу.
путей, которые в совокупности содержат все
ребра графа в точности по одному разу.
Доказательство
Половину нечетных вершин
обозначим  , а другую
половину —
, а другую
половину —  .
.
Пример.
Если вершины 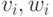
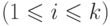 соединены
ребром, то удалим из графа
соединены
ребром, то удалим из графа  ребро (
ребро ( 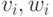 ). Если вершины
). Если вершины  не соединены ребром, то добавим к
не соединены ребром, то добавим к  ребро (
ребро ( 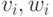 ). Все вершины нового графа будут четными, то есть
в новом графе найдется эйлеров цикл. При восстановлении графа
). Все вершины нового графа будут четными, то есть
в новом графе найдется эйлеров цикл. При восстановлении графа  цикл
разобьется на
цикл
разобьется на  отдельных путей, содержащих все ребра графа.
отдельных путей, содержащих все ребра графа.
Эйлеровым графом может быть план выставки. Это позволяет так расставить указатели маршрута, чтобы посетитель смог пройти по каждому залу в точности по одному разу.