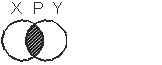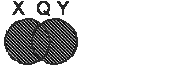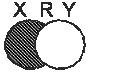| Киргизстан |
Математические методы описания моделей конструкций РЭС. Некоторые понятия теории множеств
16.2. Действия над множествами
Над множествами, как и над другими математическими величинами, можно производить некоторые действия, например, выполнять пересечение множеств, их объединение, вычитание, находить дополнение, декартово произведение и прочее.
Пересечением множеств  и
и  называют новое множество
называют новое множество  , которое образуется из элементов, одновременно общих и множеству
, которое образуется из элементов, одновременно общих и множеству  , и множеству
, и множеству  . Это можно показать так:
. Это можно показать так:
Пересечение множеств  и
и 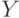 записывают следующим образом:
записывают следующим образом:
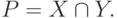
Это свойство носит название " конъюнкция" или "логическое умножение".
Если рассматривают пересечение нескольких множеств 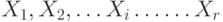 , то математическая запись имеет вид
, то математическая запись имеет вид
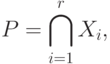
где  - число пересекающихся множеств.
- число пересекающихся множеств.
Операция пересечения множеств подчиняется переместительному закону, т.е. 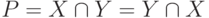 .
.
Если множества  и
и 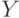 не пересекаются, то
не пересекаются, то 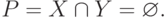
С помощью операции пересечения множеств можно, например, выявить множество типоразмеров конструктивных элементов, общих печатным платам  и
и  , или множество межплатных соединений для печатных плат
, или множество межплатных соединений для печатных плат  и
и  , т.е. выявить любые множества, обладающие какими-либо общими свойствами.
, т.е. выявить любые множества, обладающие какими-либо общими свойствами.
Объединение множеств X и Y приводит к образованию нового множества  , которое получается из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств
, которое получается из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств  или
или  .
.
На рисунке это можно представить так:
Заштрихованная область - множество  .
.
Математически объединение множеств  и
и 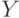 записывают следующим образом:
записывают следующим образом:

Это свойство носит название " дизъюнкция" или "логическое сложение".
Если рассматривать объединение нескольких множеств, то запись примет вид
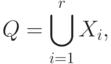
где  - число объединяемых множеств.
- число объединяемых множеств.
Операция объединения множеств, также как и операция пересечения, подчиняется переместительному закону.
С помощью этой операции можно подсчитать, например, число типоразмеров конструктивных элементов для печатных плат  и
и 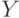 или общее число внешних электрических соединений печатных плат
или общее число внешних электрических соединений печатных плат  и
и  .
.
Разность множеств X и Y есть новое множество  , которое образуется из элементов множества
, которое образуется из элементов множества  за исключением элементов, принадлежащих одновременно множеству
за исключением элементов, принадлежащих одновременно множеству  .
.
На рис. 16.3.  - заштрихованная область.
- заштрихованная область.
Математически разность множеств  и
и 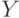 можно записать следующим образом:
можно записать следующим образом:
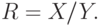
С помощью этой операции можно выявить сугубо индивидуальные признаки объекта, например, число типоразмеров конструктивных элементов, принадлежащих только плате  .
.
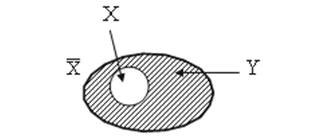
Дополнением (или отрицанием) множества  по отношению к множеству
по отношению к множеству  называют множество
называют множество  , состоящее из элементов множества
, состоящее из элементов множества  , не принадлежащих множеству
, не принадлежащих множеству  .
.
Схематически это изображается так (рис. 16.4):
Множество  - заштрихованная область. Двойное "отрицание" приводит к равенству множества самому себе:
- заштрихованная область. Двойное "отрицание" приводит к равенству множества самому себе:  .
.
С помощью операции дополнения множества можно выявить все дополнительные недостающие признаки проектируемого изделия и подвергнуть их анализу.
Декартовым произведением множеств  и
и 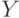 называют множество
называют множество 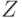 упорядоченных пар
упорядоченных пар  , образованных элементами множеств
, образованных элементами множеств  и
и  :
:
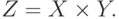
На рис. 16.5 декартово произведение множеств 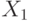 и
и 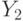 показано в виде заштрихованной области множества паросочетаний.
показано в виде заштрихованной области множества паросочетаний.
Декартово произведение двух множеств используют для исследования всевозможных паросочетаний.
Декартово произведение нескольких множеств
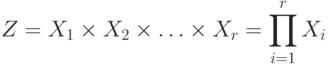
представляет собой множество r - строчек, каждая из которых образуется упорядоченной композицией элементов исходных множеств, т.е.
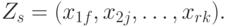
Операция декартова произведения множеств не обладает переместительным свойством, т.е. 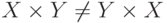 .
.
Разбиением множества  называют такое множество множеств
называют такое множество множеств 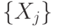 , где
, где  , а
, а 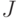 - некоторое множество индексов
- некоторое множество индексов  , при котором:
, при котором:
-
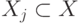 при всех
при всех  ;
; -
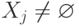 при всех
при всех  ;
; -
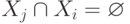 при
при 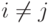 ;
; -
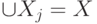 . при
. при  .
.
Это можно прочитать так:
- все подмножества
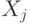 принадлежат исходному множеству
принадлежат исходному множеству  ;
; - все подмножества
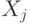 не равны пустому множеству, т.е. обязательно должны содержать элементы;
не равны пустому множеству, т.е. обязательно должны содержать элементы; - сами подмножества не должны пересекаться, т.е. их пересечение равно пустому множеству ;
- объединение всех подмножеств должно быть равно исходному множеству
 .
.
Ряд прикладных задач разбиения множества конструктивных элементов высокого уровня на элементы более низкого уровня (например, задача разбиения множества микросхем блока РЭС на отдельные субблоки) сводится к операциям разбиения множеств.
Понятие пустого множества  аналогично нулю в алгебре чисел. Действительно, если для любого числа "
аналогично нулю в алгебре чисел. Действительно, если для любого числа "  " справедливо
" справедливо 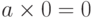 и
и 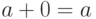 , то для любого множества
, то для любого множества  справедливо
справедливо  и
и 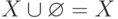 .
.
Существует понятие множества  , соответствующее единице в алгебре чисел. Такое множество обладает тем свойством, что пересечение с ним любого множества
, соответствующее единице в алгебре чисел. Такое множество обладает тем свойством, что пересечение с ним любого множества  даёт в результате это же множество
даёт в результате это же множество  , т.е.
, т.е. 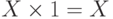 по аналогии с
по аналогии с 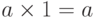 .
.
Множество  , обладающее этим свойством, называют универсальным или единичным множеством. В общем случае, если при некотором рассмотрении участвуют только подмножества некоторого фиксированного множества
, обладающее этим свойством, называют универсальным или единичным множеством. В общем случае, если при некотором рассмотрении участвуют только подмножества некоторого фиксированного множества  , то это самое большое множество и является универсальным.
, то это самое большое множество и является универсальным.
В конкретных приложениях в качестве универсального множества могут использоваться различные общие подмножества.
Пример. Среди множества комплектов конструкторских документов на изготовление изделий РЭС полный комплект конструкторских документов на изготовление изделий является универсальным множеством этих документов или когда при рассмотрении множеств микросхем отдельных субблоков РЭС выделяют универсальное множество таких микросхем на всю данную радиоэлектронную систему в целом.
Универсальное множество обладает свойством, не имеющим аналога в алгебре чисел, а именно: для любого множества  справедливо соотношение
справедливо соотношение  .
.
В объединение этих множеств должны входить как элементы множества  , так и дополняющие элементы множества
, так и дополняющие элементы множества  . Но, в свою очередь, все элементы множества
. Но, в свою очередь, все элементы множества  входят в универсальное множество
входят в универсальное множество  , поэтому и объединение
, поэтому и объединение  равно универсальному множеству
равно универсальному множеству  .
.
На основании этих рассуждений определяют дополнение множества  как
как 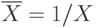 . Двойное дополнение
. Двойное дополнение 
С помощью операции дополнения можно в удобном виде представить разность множеств
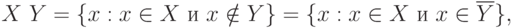
т.е.
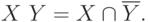
Многие определения теории множеств записывают в виде математических выражений, содержащих некоторые логические символы.
К числу таких символов относится символ следствия (импликации) "  ".
".
Например, запись  и
и  (транзитивность) читается так: если
(транзитивность) читается так: если  и
и 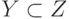 , то
, то 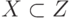 .
.
Другие символы связаны с применением кванторов общности и кванторов существования.
Квантор общности - это операция, которая сопоставляет  высказыванию: " Все
высказыванию: " Все 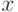 обладают свойством
обладают свойством  ". Для этой операции употребляют знак "
". Для этой операции употребляют знак " 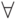 ".
".
Например, запись  свидетельствует о том, что все объекты, обладающие свойством
свидетельствует о том, что все объекты, обладающие свойством  , обладают и свойством
, обладают и свойством 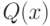 .
.
Квантор существования утверждает, что существует по крайней мере один объект  , обладающий одновременно свойствами
, обладающий одновременно свойствами  и
и 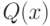 , т.е.
, т.е.  и
и 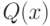 пересекаются:
пересекаются:
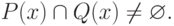
Квантор существования обозначается "  " и записывается так:
" и записывается так:
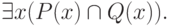 |
( x) )) |
В теории множеств используется понятие логической эквивалентности (в смысле то же самое, что и …), обозначаемой "  ". Например, запись
". Например, запись
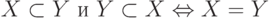
нужно читать: " Выполнение условий  и
и 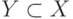 то же самое, что и
то же самое, что и 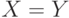 " или: " Выполнение условий
" или: " Выполнение условий  и
и 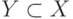 равносильно
равносильно 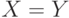 ".
".