| Киргизстан |
Размещение элементов электрической схемы
Основное назначение лекции - показать работу алгоритмов размещения элементов электрических схем на конкретных примерах для лучшего усвоения материала.
20.1. Общая постановка задачи
Задачи размещения элементов и трассировки их соединений тесно связаны и при обычных, "ручных", методах конструирования решаются одновременно. В процессе размещения элементов уточняются трассы соединений, после чего положение некоторых элементов может корректироваться. В зависимости от принятой конструктивно - технологической и схемотехнической базы при решении этих задач используются различные критерии и ограничения. Однако все конкретные разновидности упомянутых задач связаны с проблемой оптимизации схем соединений. В результате получается точное пространственное расположение отдельных элементов конструктивного узла и геометрически определённый способ соединений выводов этих элементов.
Конструкции узлов современных электронных устройств - в значительной степени унифицированные единицы. Основным элементом является коммутационная часть, определяющая конструктивно - технологический способ реализации соединений.
Критерии качества и ограничения, связанные с конкретными задачами размещения и трассировки, опираются на конкретные конструктивные и технологические особенности реализации коммутационной части узла. Всю совокупность критериев и ограничений можно разделить на две группы в соответствии с метрическими и топологическими параметрами конструкции узлов и схем.
К метрическим параметрам относятся размеры элементов и расстояния между ними, размеры коммутационного поля, расстояния между выводами элементов, допустимые длины соединений и т.д.
Топологические параметры в основном определяются принятым в конкретной конструкции способом устранения пересечений соединений и относительным расположением соединений на коммутационном поле. К ним относятся: число пространственных пересечений соединений, число межслойных переходов, близость расположения друг к другу тепловыделяющих элементов или несовместимых в электромагнитном отношении элементов и соединений.
В конкретных задачах указанные параметры в различных сочетаниях могут быть либо главными критериями оптимизации, либо выступать в качестве ограничений.
Совместное решение задач размещения и трассировки представляет значительные трудности ввиду сложного характера взаимосвязи между отдельными параметрами конструкции и схем соединений. В связи с этим при алгоритмическом подходе к их решению они рассматриваются, как правило, раздельно. Сначала осуществляется размещение элементов, а затем трассировка межсоединений. Если необходимо, этот процесс может быть повторен при другом расположении отдельных элементов.
Основной целью размещения считают создание наилучших условий для последующей трассировки соединений при удовлетворении основных требований, обеспечивающих работоспособность схем.
В общем виде задачи размещения элементов узла описывают следующим образом.
Дано множество конструктивных элементов, связанных между собой в соответствии с принципиальной электрической схемой узла. Требуется разместить элементы на некотором плоском коммутационном поле (КП) таким образом, чтобы некоторый функционал достигал экстремального значения.
Вариантами КП могут быть: панель с проводными соединениями, печатная плата, подложка микросборки, кристалл БИС.
При конструктивно однотипных элементах позиции для их установки на КП фиксированы, расположены в узлах прямоугольной решётки и могут быть описаны следующей системой параметров: 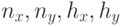 , где
, где
-
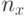 - число позиций в горизонтальном ряду;
- число позиций в горизонтальном ряду; -
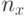 - число позиций в вертикальном ряду;
- число позиций в вертикальном ряду; -
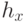 - горизонтальный шаг между позициями ;
- горизонтальный шаг между позициями ; -
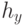 - вертикальный шаг между позициями.
- вертикальный шаг между позициями.
Возможные конструктивные особенности КП, связанные с расположением контактов элементов и внешних выводов узла, могут быть определены дополнительным набором параметров: координатами контактных площадок относительно центров позиции 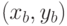 и т.д.
и т.д.
При конструировании печатных плат с разногабаритными навесными элементами, подложек гибридных ИС, а также топологии твердотельных ИС и БИС с одним слоем коммутации позиции для размещения элементов заранее не фиксированы и окончательно определяются после трассировки соединений. Характерной особенностью задач размещения в этих конструкциях является необходимость учёта разногабаритности отдельных элементов, требований минимизации суммарной площади, занимаемой схемой, и ограничений по числу внутренних пересечений.
Раздельное решение задач размещения и трассировки приводит, как правило, к неудовлетворительным результатам. Конструирование топологии таких схем обычными методами сводится к методу "проб и ошибок", а автоматизация этого процесса основана на использовании методов топологического анализа схем и интерактивных систем графического взаимодействия конструктора с ЭВМ.
Последовательное решение задач размещения и трассировки, учитывая сложность их совместного решения, оправдано в конструкциях с высокой степенью унификации размеров элементов и соединений. Примерами являются следующие конструкции: узлы, состоящие из микросхем, соединённых с помощью двусторонних или многослойных печатных плат; панели с проводным и печатным монтажом, объединяющие конструктивно унифицированные узлы низшего уровня. Для таких конструкций обычно удаётся выделить главный критерий при оптимизации размещения, учитывая остальные параметры в виде набора дополнительных ограничений.
Критерием в большинстве случаев является критерий минимума взвешенной длины (МСВД) соединений, который интегральным образом учитывает многочисленные требования, предъявляемые к расположению элементов и трасс их соединений. Это обуславливается рядом факторов:
- уменьшение длин соединений улучшает электрические параметры схемы;
- чем меньше суммарная длина соединений, тем, в среднем, проще их реализация в процессе трассировки;
- уменьшение суммарной длины соединений снижает трудоёмкость изготовления монтажных схем, особенно схем проводного монтажа;
- данный критерий относительно прост с математической точки зрения и позволяет косвенным образом учитывать другие параметры схем путем присвоения весовых оценок отдельным соединениям.
20.2. Общая характеристика алгоритмов размещения
Задача размещения элементов является одной из основных задач конструкторского этапа проектирования электронных устройств и состоит в определении оптимального пространственного расположения элементов на коммутационном поле. В качестве критериев оптимальности размещения могут быть приняты различные характеристики схемы соединений элементов или конструкции узла в целом. В большинстве случаев выбирается один главный критерий, в наилучшей степени учитывающий многочисленные конструктивные и технологические требования. Классическим критерием является критерий минимума суммарной длины соединений (МСД). Однако для определённого класса конструкций печатных плат и интегральных схем первостепенными могут стать такие критерии, как число пересечений соединений, число слоёв коммутации и т.д.
Всю совокупность алгоритмов размещения можно разделить на следующие основные группы:
- алгоритмы решения математических задач, являющихся моделями задачи размещения;
- конструктивные алгоритмы начального размещения;
- итерационные алгоритмы улучшения начального варианта размещения;
- непрерывно - дискретные методы размещения.
К первой группе относится, прежде всего, метод ветвей и границ для задачи квадратичного назначения, к которой при определённых упрощениях сводится задача размещения: набор позиций считается фиксированным, элементы рассматриваются как геометрические точки, схема соединений представляется взвешенным графом соединений.
Другой класс моделей связан с оптимизацией размещения на непрерывной плоскости, когда набор позиций для установки заранее не фиксирован.
Третья и четвёртая группы включают приближённые алгоритмы, в основном предназначенные для оптимизации размещения элементов в фиксированном наборе позиций.
Характерной особенностью конструктивных алгоритмов является то, что они создают размещение. Итерационные алгоритмы предполагают задание начального размещения.
Конструктивные алгоритмы используют последовательный или параллельно - последовательный процесс установки элементов в позиции при локальной оптимизации функции - критерия размещения.
В итерационных алгоритмах производится переразмещение элементов или их групп с целью минимизации выбранного критерия. Эти алгоритмы требуют существенных затрат машинного времени и используются для получения окончательного размещения.
Основной областью применения непрерывно - дискретных методов размещения являются конструкции, в которых позиции для установки элементов заранее не фиксированы. Исходной базой для построения алгоритмов данной группы являются непрерывные модели и механические аналогии задачи размещения.
20.3. М М задачи размещения. Модель квадратичного назначения
Пусть, даны элементы 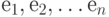 и для каждой пары элементов заданы весовые коэффициенты
и для каждой пары элементов заданы весовые коэффициенты 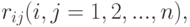 определяющие " степень связи " элементов друг с другом.
Таким образом, считаем, что схема задана матрицей соединений
определяющие " степень связи " элементов друг с другом.
Таким образом, считаем, что схема задана матрицей соединений
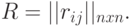 |
( 20.1) |
Пусть, имеется некоторый фиксированный набор позиций для размещения элементов 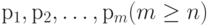 . В дальнейшем будем полагать, что
. В дальнейшем будем полагать, что  .
.
Если 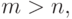 можно ввести
можно ввести 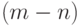 фиктивных элементов, не имеющих соединений с остальными элементами
фиктивных элементов, не имеющих соединений с остальными элементами 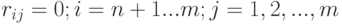 .
.
Определим расстояние 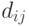 между парами позиций.
Для этого воспользуемся дополнительной информацией. Пусть, на коммутационном поле фиксированы позиции для размещения элементов.
Для них можно задать матрицу расстояний
между парами позиций.
Для этого воспользуемся дополнительной информацией. Пусть, на коммутационном поле фиксированы позиции для размещения элементов.
Для них можно задать матрицу расстояний
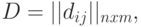 |
( 20.2) |
в которой элемент 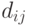 равен расстоянию между центрами позиций
равен расстоянию между центрами позиций 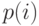 и
и  . Матрица
. Матрица  - симметричная, с нулевой главной диагональю
- симметричная, с нулевой главной диагональю  .
.
Рассмотрим такой фиксированный набор позиций (рис. 20.1):
Для такого набора позиций имеем :

Для вычисления элементов матрицы  использована ортогональная метрика,
причём расстояние между соседними позициями по вертикали и горизонтали равно 1.
использована ортогональная метрика,
причём расстояние между соседними позициями по вертикали и горизонтали равно 1.
Произвольное размещение элементов в позициях представляет собой некоторую перестановку 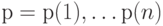 , где
, где 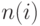 задает номер позиции, присвоенной
задает номер позиции, присвоенной  - тому элементу.
Таким образом, имеется всего
- тому элементу.
Таким образом, имеется всего  ! различных вариантов размещения элементов.
! различных вариантов размещения элементов.
Попытки найти оптимальный вариант полным перебором безуспешны даже при малых значениях  .
.
Рассмотрим задачу минимизации суммарной взвешенной длины (МСВД) соединений при следующих предположениях.
Соединения считаем условно исходящими из геометрических центров элементов.
Кроме того, предполагаем совпадение центров элементов и позиций.
Как правило, при решении задачи размещения необходимо учитывать предварительное закрепление некоторых элементов в позициях и
соединения элементов с внешними выводами. Сопоставляя внешним выводам элемент 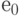 и фиксируя расположение части элементов, получим упрощенное представление коммутационного поля (рис. 20.2).
и фиксируя расположение части элементов, получим упрощенное представление коммутационного поля (рис. 20.2).
Очевидно, что длина соединений между элементами  и
и  оценивается величиной
оценивается величиной
 |
( 20.3) |
Обозначим через 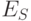 множество всех фиксированных элементов, включая элемент
множество всех фиксированных элементов, включая элемент 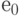 ; тогда суммарная взвешенная длина соединений элемента
; тогда суммарная взвешенная длина соединений элемента  с элементами из
с элементами из 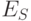 оценивается по формуле:
оценивается по формуле:
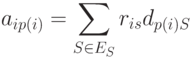 |
( 20.4) |
где  - расстояние между элементом
- расстояние между элементом 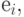 находящимся в позиции
находящимся в позиции 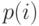 , и элементом
, и элементом  .
.
Учитывая вышесказанное, а также симметричность матриц  и
и  , запишем выражение для суммарной вешенной длины соединений при произвольном размещении:
, запишем выражение для суммарной вешенной длины соединений при произвольном размещении:
 |
( 20.5) |
Таким образом, задача размещения по критерию МСВД соединений состоит в минимизации функционала (19.5) на множестве перестановок Р.
Данная задача является вариантом общей математической модели, получившей название задачи квадратичного назначения.