| Киргизстан |
Размещение элементов электрической схемы
20.4. Алгоритмы последовательного размещения элементов по связности
Исходной информацией для размещения элементов является:
Прежде всего, рассмотрим наиболее представительные алгоритмы, использующие последовательный процесс установки элементов в позиции.
Пусть,  - множество элементов, подлежащих размещению, а
- множество элементов, подлежащих размещению, а  - множество позиций для их установки.
- множество позиций для их установки.
Вводится  - шаговый процесс принятия решений, на каждом шаге которого выбирается один из
неразмещённых элементов и помещается в одну из незанятых позиций.
- шаговый процесс принятия решений, на каждом шаге которого выбирается один из
неразмещённых элементов и помещается в одну из незанятых позиций.
Структура любого последовательного алгоритма размещения определяется правилами выбора очередного элемента и позиции для его установки.
Пусть,  - элементы, размещённые до
- элементы, размещённые до  - го шага, а
- го шага, а  - позиции, занятые этими элементами;
- позиции, занятые этими элементами;  и
и  - соответственно, неразмещённые элементы и незанятые позиции.
- соответственно, неразмещённые элементы и незанятые позиции.
Перед началом размещения могут быть две ситуации:
- нет размещённых ранее элементов, внешние выводы узла (контакты, разъёмы и т.п.) не закреплены (в этом случае в алгоритме должен быть особо определён способ установки первого элемента);
- имеется группа заранее размещённых элементов или закреплённых внешних выводов.
В основу большинства последовательных алгоритмов размещения положен принцип оптимизации целевой функции, сводящийся к выбору на данном шаге локально оптимальной позиции для одного из элементов при неизменности положения ранее размещенных элементов.
Поскольку критерий минимума суммарной длины соединений наиболее распространён, он и будет рассмотрен при описании алгоритмов данной группы.
Рассмотрим последовательный алгоритм по связности. В алгоритмах размещения по связности элемент и позиция выбираются независимо.
Выбор элемента
Любое правило выбора элемента для размещения основано на вычислении "меры связности" ещё не размещённых элементов с уже размещёнными.
Мерой связности двух элементов  и
и  является количество соединений между ними, заданное в матрице соединений
является количество соединений между ними, заданное в матрице соединений  Существуют различные способы расчёта значений
Существуют различные способы расчёта значений 
Так, в алгоритмах " попарных связей " для каждого неразмещённого элемента 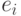 подсчитывается характеристика
подсчитывается характеристика
 |
( 20.6) |
причем,  рассчитывается по формуле
рассчитывается по формуле
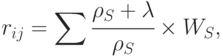 |
( 20.7) |
в которой  - множество цепей, связывающих элементы
- множество цепей, связывающих элементы 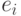 и
и  ;
;
 - размер цепи;
- размер цепи;
 - весовой коэффициент;
- весовой коэффициент;
 - целочисленный параметр.
- целочисленный параметр.
Параметр  позволяет дифференцировать вклад цепей различного размера.
Чем больше значение
позволяет дифференцировать вклад цепей различного размера.
Чем больше значение  , тем больше влияние цепей с малым значением
, тем больше влияние цепей с малым значением 
Очередным размещённым элементом является элемент, имеющий максимальную характеристику (20.6), т.е. выбор элемента осуществляется по наибольшему числу связей с уже размещёнными элементами.
Существует и другое правило выбора очередного размещаемого элемента, основанное на оценке числа связей размещаемого элемента  как с размещёнными, так и с неразмещёнными элементами (характеристика абсолютной связности ):
как с размещёнными, так и с неразмещёнными элементами (характеристика абсолютной связности ):
 |
( 20.8) |
}В этом случае выбирается элемент с максимальным значением 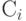 (20.8) (данный выбор аналогичен принципу максимальной конъюнкции - минимальной дизъюнкции, применяемому в алгоритмах компоновки).
(20.8) (данный выбор аналогичен принципу максимальной конъюнкции - минимальной дизъюнкции, применяемому в алгоритмах компоновки).
К этому же типу относится характеристика относительной связности:
 |
( 20.9) |
На очередном шаге алгоритма размещается элемент, имеющий максимальный коэффициент относительной связности.
Рассмотренные характеристики не зависят от положений элементов, поэтому в принципе может быть выполнено предварительное упорядочение всех элементов, а потом уже и их размещение.
Рассмотрим исходную матрицу смежности с элементом x_{0}, который в нашем случае содержит клеммы К1, К2, К3, К4 (рис. 20.2). Он является уже фиксированным элементом, поэтому размещать остальные элементы будем по отношении к нему.
Первый шаг.

Максимальную характеристику имеет элемент  , следовательно, его размещаем вторым.
Имеем:
, следовательно, его размещаем вторым.
Имеем: 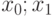 .
.
Второй шаг. Расчет проводим с учетом этих двух размещенных элементов:

Макимальную характеристику имеет элемент 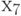 , поэтому его размещаем третьим.
Имеем:
, поэтому его размещаем третьим.
Имеем:  .
.
Третий шаг. Произведём расчёт с учётом уже трёх размещённых элементов:

Максимальную характеристику имеет элемент  , поэтому шестой элемент размещаем четвёртым. Имеем:
, поэтому шестой элемент размещаем четвёртым. Имеем: 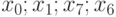 .
.
Четвертый шаг. Производим расчет с учетом четырех размещенных элементов:

Максимальную характеристику имеет элемент 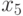 , его размещаем пятым. Имеем:
, его размещаем пятым. Имеем:  .
.
Пятый шаг. Производим расчет с учетом уже пяти размещенных элементов.

Максимальную характеристику имеет элемент 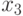 , следовательно, третий элемент размещаем шестым.
Имеем:
, следовательно, третий элемент размещаем шестым.
Имеем:  .
.
Шестой шаг. Производим расчет с учетом уже шести размещенных элементов.

Максимальную характеристику имеет элемент 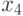 , следовательно, его размещаем седьмым.
, следовательно, его размещаем седьмым.
Окончательная последовательность размещения будет такой:


