Математические методы описания моделей конструкций РЭС. Некоторые понятия теории множеств

16.5. Отображение множеств

Одним из основных понятий теории множеств является понятие отображения.

Если заданы два непустых множества и , то закон, согласно которому каждому элементу 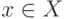ставится в соответствие элемент , называют однозначным отображением в или функцией, определённой на и принимающей значение на .

Существуют и многозначные отображения множества на множестве , которые определяют закон, согласно которому каждому элементу 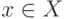ставится в соответствие некоторое подмножество 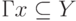, называемое образом элемента . Возможны случаи, когда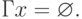

Пусть, задано некоторое подмножество 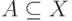. Для любого 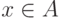образом является подмножество .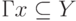

Совокупность всех элементов , являющихся образами для всех 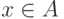, называют образом множества и обозначают .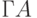

В этом случае .

Рассмотрим некоторые свойства отображений.

Если заданы два подмножества 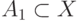и 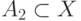, то для отображения объединения этих подмножеств используют

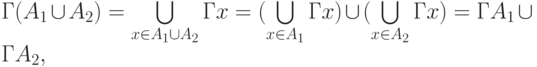
т.е.

При отображении пересечения этих подмножеств 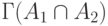соотношение

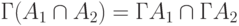
справедливо только в том случае, когда отображение является однозначным. В общем случае имеет место выражение

В практических приложениях теории множеств широко распространены многократные отображения, получаемые на одном и том же множестве элементов.

Пусть, 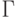и - отображения множества в .

Произведением (композицией) этих отображений называют отображение 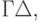которое, согласно свойству ассоциативности композиции, определяют так:

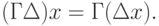
Для многокритериального отображения множества в , когда 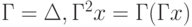; 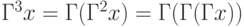и так далее.

В общем случае Тогда .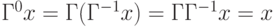

Приведённая запись означает, что 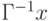представляет собой обратное отображение, а .

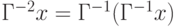Между отображением и функцией имеется некоторое различие, характеризуемое способом определения этих отношений на множестве , причём отображение рассматривают как частный случай функции.

Функциональное отношение 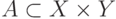называют отношением множества в , если это отношение всюду определено на , т.е. его область определения 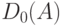совпадает с множеством .

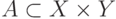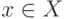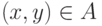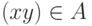Отношение называют функциональным, если все его элементы (упорядоченные пары) имеют различные первые координаты, т.е. каждому элементу , такому, что , соответствует один и только один элемент . При этом первая координата " " упорядоченной пары является аргументом (переменной), а вторая " " - образом (значением) функции.

Например, во множестве 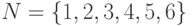заданы соотношения:

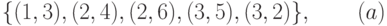
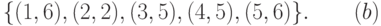
Какие из этих отношений являются функциями, а какие - отображениями?

В выражениях (a) и (b) первое отношение является отображением, второе - функцией, так как для второго отношения все первые координаты отличны друг от друга, а для первого это условие не выполняется.

Рассмотрим пример конструирования печатной платы.

Пусть, - некоторое исходное расположение конструктивных элементов на плате; - множество различных расположений таких элементов на плате. Тогда 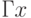для любого 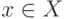- множество положений, которое можно получить из , например, с помощью парных перестановок конструктивных элементов, делая один шаг перестановок в направлении улучшения некоторого показателя качества размещения. При этом 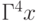- множество перестановок конструктивных элементов, которые можно выполнить из состояния четырьмя шагами; - множество положений (состояний) конструктивных элементов, из которых данное положение может быть получено за один шаг.

Если из положения перестановками с другими элементами не удаётся улучшить показатель качества размещения (достичь локальный оптимум показателя качества), то .

Контрольные вопросы

1. Что называют множеством?
2. Назовите способы задания множеств.
3. Является ли множеством запись ?
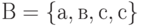4. В каком случае множество считается заданным?
5. Приведите примеры множеств для РЭС.
6. Запишите множество через его элементы.
7. Что указывает описательный способ задания множеств?
8. Запишите на языке теории множеств: во множестве элементов сложной РЭС имеется некоторое множество микросхем.
9. Что называют мощностью множества?
10. Как обозначается пустое множество?
11. Запишите символами: элемент принадлежит множеству .
12. Запишите символами: множество является подмножеством множества .
13. Что называется пересечением множеств?
14. Что называется объединением множеств?
15. Что называется разностью множеств?
16. Что называется дополнением множеств?
17. Что называется декартовым произведением множеств?
18. Что представляет собой операция " квантор общности "? Как она записывается?
19. Что представляет собой операция " квантор существования "? Как она записывается?
20. Как записываются законы коммутативности?
21. Как записываются законы ассоциативности?
22. Как записываются законы дистрибутивности?
23. Как записываются законы идемпотентности?
24. Как записываются законы де Моргана?
25. Перечислите виды отношений и их свойства.
26. Что называют однозначным отображением множеств?
27. Что называют многозначным отображением множеств?