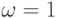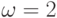Проверка по отношению правдоподобия в случае трех решений
Во многих задачах выбора решений в условиях неопределенности
окончательному выбору могут предшествовать несколько стадий оценки
текущего состояния природы. При этом на последующих стадиях применяются
более точные (и обычно более дорогие) схемы проведения испытаний.
Ограничим наше рассмотрение случаем, когда возможны лишь две такие стадии.
При этом начальная стадия включает проведение некоторого испытания и
принятие (на основании полученных результатов) одного из трех
решений. Первые два решения соответствуют выбору одной из двух простых
гипотез. Третий вариант предполагает проведение дополнительных
испытаний, завершающихся окончательным выбором гипотезы. Примем, что
реализация третьего варианта передается другому исполнителю. Ожидаемые
потери для этого случая будем считать известными.
Таким образом, мы рассматриваем операцию, в которой m=2, 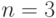 и матрица потерь задана коэффициентами из
табл. 4.5.
и матрица потерь задана коэффициентами из
табл. 4.5.
Таблица
4.5.
| Матрица потерь |
Решения статистика |
|
Состояния природы
|
a=1 |
a=2 |
a=3 |
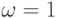 |
0 |
w12 |
w13 |
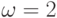 |
w21 |
0 |
w23 |
При этом, согласно (17.9)-(17.11) и (17.16),
значения апостериорного риска 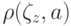 ,
соответствующие решению a=d(z), определяются следующими
формулами:
,
соответствующие решению a=d(z), определяются следующими
формулами:
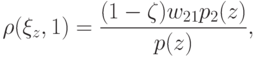 |
(
19.10)
|
 |
(
19.11)
|
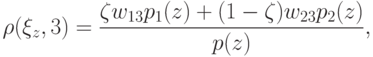 |
(
19.12)
|
где
p(z) из (17.11) и

из (18.2).
Далее, в соответствии с (17.20), байесовское решение
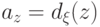
определяется условиями:
Эти условия (после подстановки в них правых частей из
выражений (9.10)-(9.12)) преобразуются к виду:
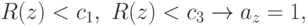 |
(
19.13)
|
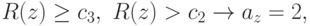 |
(
19.14)
|
где
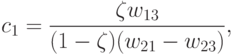 |
(
19.15)
|
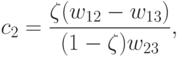 |
(
19.16)
|
и символ
R(z) соответствует
отношению правдоподобия, т.е.
Заметим, что применимость третьего решения предполагает выполнение условия 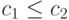 , которое эквивалентно следующему неравенству для
коэффициентов матрицы потерь:
, которое эквивалентно следующему неравенству для
коэффициентов матрицы потерь:
 |
(
19.17)
|
Условимся, что
неравенство (19.17) является справедливым.
Тогда неравенства c1<c3<c2 также являются
справедливыми, что устанавливается непосредственной проверкой. Поэтому в
условиях (19.13) достаточно выполнения лишь первого неравенства, а
в условиях (19.14) - второго неравенства.
Таким образом, в рассмотренном случае ( m=2, n=3 )
байесовский критерий  сводится к следующей модификации проверки по
отношению правдоподобия:
сводится к следующей модификации проверки по
отношению правдоподобия:
где
![I_1 = [0, c_1),\quad I_2 = (c_2,\infty),\quad I_3 = [c_1, c_2]](/sites/default/files/tex_cache/f3049552da8ba6b406a798b8f7def6d5.png) |
(
19.18)
|
и
c1,
c2 соответственно из (19.15), (19.16).
 и матрица потерь задана коэффициентами из
табл. 4.5.
и матрица потерь задана коэффициентами из
табл. 4.5.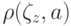 ,
соответствующие решению a=d(z), определяются следующими
формулами:
,
соответствующие решению a=d(z), определяются следующими
формулами: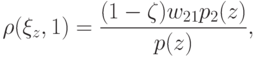

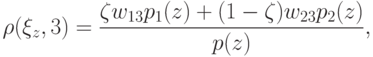
 из (18.2).
Далее, в соответствии с (17.20), байесовское решение
из (18.2).
Далее, в соответствии с (17.20), байесовское решение 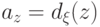 определяется условиями:
определяется условиями: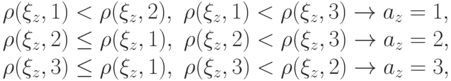
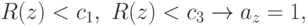
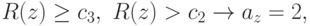
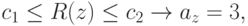
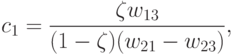
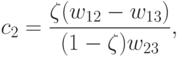
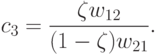
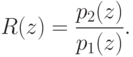
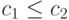 , которое эквивалентно следующему неравенству для
коэффициентов матрицы потерь:
, которое эквивалентно следующему неравенству для
коэффициентов матрицы потерь:
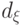 сводится к следующей модификации проверки по
отношению правдоподобия:
сводится к следующей модификации проверки по
отношению правдоподобия: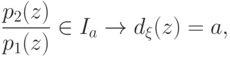
![I_1 = [0, c_1),\quad I_2 = (c_2,\infty),\quad I_3 = [c_1, c_2]](/sites/default/files/tex_cache/f3049552da8ba6b406a798b8f7def6d5.png)