| ВКР |
Многошаговые задачи выбора решений
Теперь рассмотрим случай, когда N=2 (именно этому случаю соответствует рис. 2.12), и построим матрицу (см. табл. 2.13), описывающую выигрыши (или математические ожидания выигрышей) стороны P1 в первом из двух периодов.
| Случай N=2 | Инспекцию: | |
| Нарушение: | Проводить | Не проводить |
| Совершать | -1 | 1 |
| Не совершать | 1 | v1 |
Отметим, что отказ сторон от действий в первом периоде переводит игру во второй период, характеризуемый уже рассмотренной матрицей из табл. 2.12. Поскольку, согласно (13.18), цена этой игры меньше, чем 1, то матрица из табл. 2.13 также не содержит седловых значений и ей соответствует цена игры
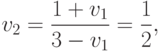 |
( 13.19) |
Аналогично, для любого значения N>1 выводим, что цена игры, соответствующей выбору действия в первый из N периодов, определяется выражением
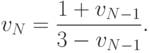 |
( 13.20) |
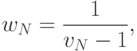 |
( 13.21) |
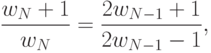
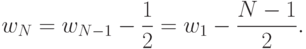 |
( 13.22) |
 ,
которое в сочетании с (13.22) дает решение
,
которое в сочетании с (13.22) дает решение
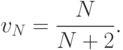
Таким образом, выбору действия в первый из N>1 (остающихся) периодов соответствует игра с матрицей из табл. 2.14. Тогда, согласно (11.7) и (11.8), оптимальные стратегии сторон P1 и P2 в первом из N периодов определяются рулетками вида
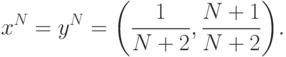 |
( 13.23) |
Следовательно, для любой из двух сторон вероятность выбора действия в первом из N периодов равна 1/(N+2). Если стороны не совершали действий ни в одном из k начальных периодов (k<N), то вероятность совершения действия в (k+1) -м периоде равна

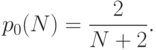
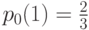 и
и 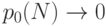 при
при 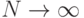 .
.Таким образом, обе схемы, использованные для анализа рассмотренного примера при N=2 (многошаговая схема и схема, основанная на предварительном построении нормальной модели), приводят к одним и тем же значениям вероятностей выбора действий и отказа от действий. Нетрудно заметить, что возможность успешного применения многошаговой схемы при произвольных значениях N>1 связана с тем, что дерево игры оказалось существенно не полным. В каждом его четном ярусе содержится ровно два узла, а в каждом нечетном - ровно один узел и три вершины (кроме первого яруса). Т.е. возможность построения рекуррентных отношений, связывающих ожидаемые выигрыши сторон на последовательных стадиях процесса принятия решений, определяется спецификой рассмотренного примера.
Замечание 2.7 (о стратегиях поведения. Рассмотренная схема последовательного выбора решений использует на каждом ходе некоторую рулетку, определенную не на множестве всех чистых стратегий (число которых может быть велико), а на множестве вариантов, имеющихся у этой стороны на конкретном ходе (число которых обычно не велико). Чтобы отличать рассмотренные комплекты рулеток от введенных ранее смешанных стратегий, их обычно называют стратегиями поведения. Таким образом, стратегия поведения конкретной стороны сопоставляет каждому информационному множеству этой стороны вероятностное распределение, заданное на наборе альтернатив, которые имеются в этом множестве.


