| ВКР |
Лекция 10: Приведение позиционной игры к игре в нормальной форме. Условия существования стратегического равновесия
Условия существования стратегического равновесия в конечной игре двух лиц
Теорема 2.1 (достаточные условия существования устойчивых
решений) Пусть  есть конечная игра двух лиц с
полной информацией и пусть S и G есть множества
стратегий, имеющихся у сторон P1 и P2 в этой игре.
Тогда произведение
есть конечная игра двух лиц с
полной информацией и пусть S и G есть множества
стратегий, имеющихся у сторон P1 и P2 в этой игре.
Тогда произведение  содержит устойчивую
стратегическую пару (s*,g*).
содержит устойчивую
стратегическую пару (s*,g*).
Доказательство
1. Поскольку  есть конечная игра
с полной информацией, то (см. определение в
"Нормальная форма конечной игры. Задание конечной игры в позиционной форме"
)
каждое информационное множество, входящее в описание ее
развернутой формы, содержит ровно один узел (точку ветвления) дерева игры.
При этом любой узел дерева, помеченный (сверху) номером первого игрока,
является точкой определения каждой стратегии
есть конечная игра
с полной информацией, то (см. определение в
"Нормальная форма конечной игры. Задание конечной игры в позиционной форме"
)
каждое информационное множество, входящее в описание ее
развернутой формы, содержит ровно один узел (точку ветвления) дерева игры.
При этом любой узел дерева, помеченный (сверху) номером первого игрока,
является точкой определения каждой стратегии  , а любой
узел, помеченный (сверху) номером второго игрока, - точкой определения
стратегии
, а любой
узел, помеченный (сверху) номером второго игрока, - точкой определения
стратегии  .
.
Каждой конкретной паре стратегий (s,g) дерево игры сопоставляет определенную этими стратегиями последовательность переходов по ребрам дерева, начинающуюся в корневой точке и заканчивающуюся в одной из вершин. Тем самым определяются значения платежных функций сторон M1(s,g) и M2(s,g), соответствующие этой паре стратегий, поскольку вершинам дерева, представляющим исходы игры, сопоставлены значения полезностей для обоих игроков.
Напомним, что реализацию операции, соответствующую заданной последовательности переходов по ребрам дерева (т.е. пути в дереве игры ), мы назвали партией игры. В качестве иллюстрации, на рис. 2.2 широкими линиями отмечен путь, соединяющий точки q1, q3, q4, t5. Число позиций (узлов) в самой длинной партии игры условимся называть длиной игры. Нетрудно подсчитать, что длина игры, представленной деревом на рис. 2.2, равна 3 (причем указанный выше путь соответствует самой длинной партии игры). Проведем доказательство теоремы индукцией по длине игры.
Для игр нулевой длины будем считать теорему справедливой. Это допущение
можно интерпретировать следующим образом. Поскольку в дереве такой игры
нет ни одного узла (т.е. игра не предполагает совершение ходов игроками),
то области определения функций s и g пусты. Примем,
что в этом случае у каждой из сторон есть ровно одна стратегия и она не предполагает
принятие каких-либо решений. При этом дерево игры необходимо представлено
некоторой вершиной, которой сопоставлены выигрыши игроков. Следовательно,
платежные функции M1 и M2 существуют и определены
в единственной точке множества  . Заметим, что какие-либо
отклонения от этой единственной точки являются невозможными (в силу ее
единственности). Будем считать ее точкой равновесия в игре нулевой
длины.
. Заметим, что какие-либо
отклонения от этой единственной точки являются невозможными (в силу ее
единственности). Будем считать ее точкой равновесия в игре нулевой
длины.
Предположим, что теорема справедлива для всех конечных игр двух
лиц с полной информацией длины меньшей, чем k. Пусть  есть игра с полной информацией длины k и ее первому ходу (т.е.
позиции q1 ) соответствуют r возможных выборов, которые переводят игру
из позиции q1 соответственно в точки p1...pr
дерева игры (они могут быть узлами или вершинами дерева).
есть игра с полной информацией длины k и ее первому ходу (т.е.
позиции q1 ) соответствуют r возможных выборов, которые переводят игру
из позиции q1 соответственно в точки p1...pr
дерева игры (они могут быть узлами или вершинами дерева).
В результате дальнейшее развитие игры будет описываться переходами
в поддереве, корнем которого является одна из точек pi, 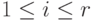 . Поддерево с корнем в точке pi является
описанием некоторой конечной подыгры
. Поддерево с корнем в точке pi является
описанием некоторой конечной подыгры 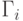 с полной информацией, имеющей
длину меньшую, чем k. Будем называть игру
с полной информацией, имеющей
длину меньшую, чем k. Будем называть игру 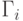 усечением исходной игры.
Заметим, что длина
усечением исходной игры.
Заметим, что длина 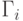 окажется
нулевой, если точка pi есть вершина исходного дерева.
В качестве иллюстрации рис. 2.6 воспроизводит дерево игры, представленное
на рис. 2.2, на котором (овальными пунктирными контурами) выделены поддеревья
игр
окажется
нулевой, если точка pi есть вершина исходного дерева.
В качестве иллюстрации рис. 2.6 воспроизводит дерево игры, представленное
на рис. 2.2, на котором (овальными пунктирными контурами) выделены поддеревья
игр 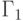 и
и 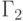 с корнями соответственно в
точках p1=q3 и p2=q2. При этом длины этих подыгр соответственно равны 2
(для
с корнями соответственно в
точках p1=q3 и p2=q2. При этом длины этих подыгр соответственно равны 2
(для 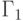 ) и 1 (для
) и 1 (для 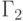 ). Заметим, что
пунктирные окружности,
выделяющие информационные множества сторон на рис. 2.2, опущены на
рис. 2.6 (поскольку известно, что в игре с полной информацией каждый узел
дерева составляет отдельное информационное множество).
). Заметим, что
пунктирные окружности,
выделяющие информационные множества сторон на рис. 2.2, опущены на
рис. 2.6 (поскольку известно, что в игре с полной информацией каждый узел
дерева составляет отдельное информационное множество).
Сужение области определения функций s и g
(определенных на соответствующих узлах дерева игры  ) до подмножеств узлов,
входящих в поддерево игры
) до подмножеств узлов,
входящих в поддерево игры 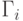 , определяет стратегии сторон P1 и P2 в этой подыгре. Будем называть их усечениями стратегий s, g и обозначать si, gi.
Множества таких стратегий обозначим соответственно Si, Gi. В целях иллюстрации отметим, что усечения стратегий s1 и s3 первого игрока в игре
, определяет стратегии сторон P1 и P2 в этой подыгре. Будем называть их усечениями стратегий s, g и обозначать si, gi.
Множества таких стратегий обозначим соответственно Si, Gi. В целях иллюстрации отметим, что усечения стратегий s1 и s3 первого игрока в игре  (см. (9.1), (9.3)), дают одну и ту же стратегию
(см. (9.1), (9.3)), дают одну и ту же стратегию  этого игрока в подыгре
этого игрока в подыгре 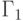 . Сужения двух других стратегий P1 ( s2 и s4 -
см. (9.2), (9.4)) в исходной игре дают его стратегию
. Сужения двух других стратегий P1 ( s2 и s4 -
см. (9.2), (9.4)) в исходной игре дают его стратегию 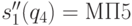 в подыгре
в подыгре 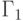 . Аналогично, сужения
стратегий (9.5)-(9.8) второго игрока
в игре
. Аналогично, сужения
стратегий (9.5)-(9.8) второго игрока
в игре  дают множество стратегий
дают множество стратегий

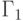 .
.Таким образом, исходной игре  сопоставляются r усеченных
игр
сопоставляются r усеченных
игр 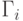 с полной информацией, имеющих длину меньшую, чем k,
и характеризуемых множествами стратегий Si, Gi,
с полной информацией, имеющих длину меньшую, чем k,
и характеризуемых множествами стратегий Si, Gi, 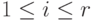 .
Любая пара стратегий сторон
.
Любая пара стратегий сторон 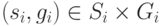 задает некоторый исход в поддереве игры
задает некоторый исход в поддереве игры 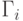 и, тем самым,
определяет значения платежей
и, тем самым,
определяет значения платежей 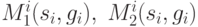 как значения полезностей, сопоставленных
соответствующей вершине дерева. При этом
как значения полезностей, сопоставленных
соответствующей вершине дерева. При этом
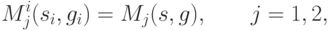 |
( 9.9) |
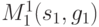 , соответствующая
игре
, соответствующая
игре 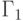 , поддерево которой изображено на
рис. 2.6, представлена в табл. 2.4.
, поддерево которой изображено на
рис. 2.6, представлена в табл. 2.4.По условию индукции, каждое
произведение  содержит устойчивую стратегическую
точку
содержит устойчивую стратегическую
точку 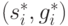 , для которой справедливы
неравенства:
, для которой справедливы
неравенства:
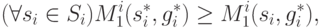 |
( 9.10) |
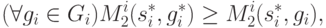 |
( 9.11) |
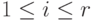 . Заметим, что эти условия остаются справедливыми
и для подыгр нулевой длины. Соответствующие
им множества Si и Gi содержат по одному элементу,
а значения
. Заметим, что эти условия остаются справедливыми
и для подыгр нулевой длины. Соответствующие
им множества Si и Gi содержат по одному элементу,
а значения 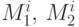 определяются, как и в общем
случае, значениями полезностей в соответствующем исходе.
определяются, как и в общем
случае, значениями полезностей в соответствующем исходе.3. Пусть в исходной игре  первый ход
(в позиции q1 ) делает игрок P1. Определим целое
число l,
первый ход
(в позиции q1 ) делает игрок P1. Определим целое
число l, 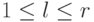 , такое, что
, такое, что
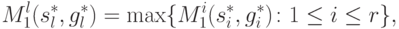 |
( 9.12) |
 , задав ее условиями
, задав ее условиями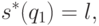 |
( 9.13) |
 |
( 9.14) |
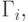
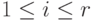 .
Введенная стратегия допускает следующую интерпретацию.
.
Введенная стратегия допускает следующую интерпретацию.На первом ходе игрок P1 решает, в какой подыгре 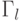 он будет участвовать на последующих ходах. При этом в соответствии
с (9.12), он выбирает ту подыгру
он будет участвовать на последующих ходах. При этом в соответствии
с (9.12), он выбирает ту подыгру 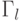 ,
в которой его выигрыш, заданный устойчивой по Нэшу парой стратегий
,
в которой его выигрыш, заданный устойчивой по Нэшу парой стратегий 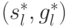 этой подыгры,
является максимальным. Все последующие ходы (в этой подыгре) он
осуществляет в соответствии со стратегией
этой подыгры,
является максимальным. Все последующие ходы (в этой подыгре) он
осуществляет в соответствии со стратегией 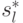 . Однако
формальное определение стратегии предполагает, что выборы
игрока P1 должны быть определены для всех его позиций в дереве
игры
. Однако
формальное определение стратегии предполагает, что выборы
игрока P1 должны быть определены для всех его позиций в дереве
игры  . Такое определение обеспечивается
условиями (9.14).
. Такое определение обеспечивается
условиями (9.14).
Теперь определим стратегию g* игрока P2
в игре  . Примем, что его выбор в позиции q из поддерева
. Примем, что его выбор в позиции q из поддерева 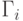 (помеченной номером этого игрока) совпадает с выбором, предписываемым
стратегией
(помеченной номером этого игрока) совпадает с выбором, предписываемым
стратегией 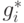 , входящей в устойчивую пару
, входящей в устойчивую пару 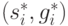 из (9.10), (9.11). То есть
из (9.10), (9.11). То есть
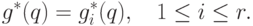 |
( 9.15) |
Покажем, что введенная пара 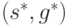 есть устойчивая стратегическая точка в
есть устойчивая стратегическая точка в  .
Из (9.9), (9.13)-(9.15) и из (9.10) следует, что
.
Из (9.9), (9.13)-(9.15) и из (9.10) следует, что

 есть любая стратегия, усечение которой
в подыгре
есть любая стратегия, усечение которой
в подыгре 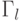 есть gl. Таким образом,
есть gl. Таким образом,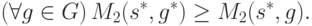 |
( 9.16) |
Аналогично, из (9.9), (9.13)-(9.15) и из (9.11), (9.12) выводим, что

 игрока P1, переводящей
продолжение игры в подыгру
игрока P1, переводящей
продолжение игры в подыгру 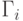 . Таким образом,
. Таким образом,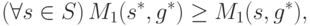
4. Случай, когда первый ход делает игрок P2, рассматривается аналогично.
Следствие 2.1. Матрица, представляющая нормальную форму конечной антагонистической игры с полной информацией, всегда имеет седловое значение.
Замечание 2.3. Примером конечной антагонистической игры с полной информацией является игра в шахматы (при условии ведения протокола). Однако чрезмерно большое число возможных позиций в шахматной игре затрудняет как построение дерева игры, так и приведение ее к нормальной форме для определения седлового значения соответствующей матрицы. Тем не менее, именно для этой игры в 1913 году Э.Цермело1Цермело Эрнест (1871-1953) - немецкий математик, автор аксиомы выбора для произвольного семейства множеств. поставил и положительно решил вопрос о существовании наилучших возможных ходов в каждой позиции (заметим, что понятия нормальной и развернутой форм игры в то время еще не были введены2Цермело Э. О применении теории множеств к теории шахматной игры // Матричные игры. М.: Физматгиз, 1961. С.167-172 (перевод с немецкого). ).


