| ВКР |
Анализ антагонистической игры на основе принципа максимума гарантированного результата
Замечание 1.18 (о бабочкообразных ядрах ). Рассмотрим частный случай, когда
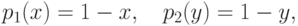
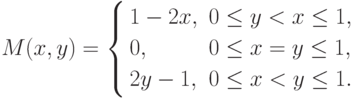 |
( 7.3) |
Разрывная поверхность, которая соответствует функции M(x,y) из (7.3), определенной на единичном квадрате  ,
, 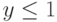 , представлена на рис.1.15. Указанная поверхность
составлена из трех частей, включающих два плоских треугольника и (изображенный жирной линией)
отрезок, который лежит на прямой x=y в плоскости M(x,y)=0.
Все части имеют общую точку (отмеченную
темным кружком). Форма поверхности напоминает бабочку, и этим определяется
использование термина " бабочкообразные ядра " применительно к
функциям вида (7.2).
, представлена на рис.1.15. Указанная поверхность
составлена из трех частей, включающих два плоских треугольника и (изображенный жирной линией)
отрезок, который лежит на прямой x=y в плоскости M(x,y)=0.
Все части имеют общую точку (отмеченную
темным кружком). Форма поверхности напоминает бабочку, и этим определяется
использование термина " бабочкообразные ядра " применительно к
функциям вида (7.2).
Оценим нижнюю цену игры и максиминную стратегию игрока P1. Воспользуемся представлением
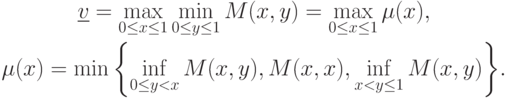 |
( 7.4) |
При этом, согласно (7.2),
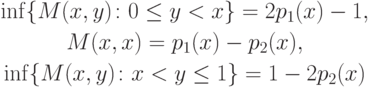
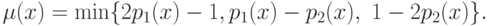 |
( 7.5) |
Определим вещественное число t как решение уравнения (см. рис.1.14):
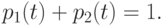 |
( 7.6) |
Заметим, что в силу (7.1), условий

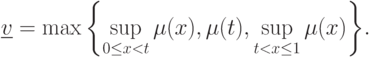 |
( 7.7) |
Из (7.6) и условия монотонности функций p1, p2 вытекает, что
 |
( 7.8) |
 |
( 7.9) |
Вычитая величину 2p2(x) из левой и правой частей неравенства (7.5), получим правое неравенство из (7.9). Теперь из (7.5) и (7.9) следует, что
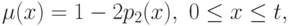
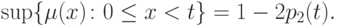 |
( 7.10) |
 |
( 7.11) |
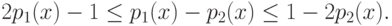 |
( 7.12) |
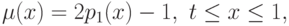
 |
( 7.13) |
Пусть теперь x=t. Тогда из (7.9) и (7.12) следует равенство
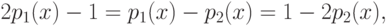 |
( 7.14) |
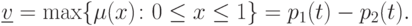 |
( 7.15) |
При этом максиминная стратегия x* игрока P1 определяется как решение уравнения (7.6), т.е. x*=t.
Аналогично определяется верхняя цена игры и минимаксная стратегия игрока P2. Запишем
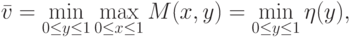 |
( 7.16) |
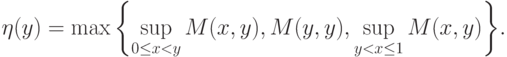
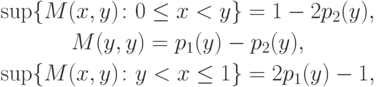
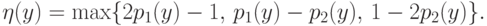 |
( 7.17) |
Теперь из (7.17), (7.9) и (7.12) выводим, что
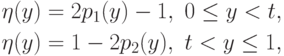
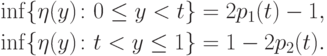
Полученные оценки в сочетании с равенством (7.14) приводят к выводу, что
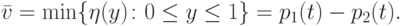 |
( 7.18) |
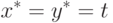 |
( 7.19) |
 из (7.6); см. рис.1.14.
из (7.6); см. рис.1.14.Совпадение верхней и нижней цен игры доказывает, что пара ( x*,y*) из (7.19) является седловой точкой ядра (7.2). Следовательно, эта пара стратегий определяет решение, обладающее свойствами равновесия по Нэшу. Полученному решению соответствует цена игры
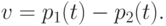 |
( 7.19) |
Еще раз отметим, что решение (7.19), (7.20) является также оптимальным по Парето. Следует также обратить внимание на то, что величина v из (7.20) есть гарантированное игроку P1 математическое ожидание полезности, а не выигрыш в конкретной реализации игры (который может иметь лишь значения из множества {-1,0,+1} ). В случае, когда цена игры v оказывается положительной (отрицательной), говорят, что игра поставлена в пользу первого (второго) игрока. При v=0 игру называют " безобидной ".
Выражение (7.20) для цены игры является важной рекомендацией. Согласно этому выражению, для постановки игры в свою пользу игрок Pi (i=1,2) должен стремиться увеличить вероятность pi(t), соответствующую упреждению t из (7.6). Как уже отмечалось, мы полагаем, что каждая из сторон знает обе функции p1, p2.
Замечание 1.19 (об играх типа дуэлей ). Модели
рассмотренного выше типа первоначально использовались как средство
описания боевых столкновений типа дуэлей (например, дуэли
истребитель-бомбардировщик, штурмовик-наземный комплекс и т.п.).
При этом функции p1(x) и p2(y) характеризуют
вероятности поражения противника при выстреле, осуществленном игроком P1
или P2 соответственно с расстояния x или  (при естественном предположении, что стреляющая сторона не была уничтожена противником еще
до своего выстрела). В теории рассмотрены случаи, когда стороны могут
последовательно осуществить несколько выстрелов, обнаруживая факты
промахов противника (в этом случае дуэль называется " шумной ") или
не имея возможностей для такого обнаружения (в этом случае говорят
о " бесшумной " дуэли). Исследования подобных моделей оказали
определенное влияние на содержание наставлений для некоторых родов войск4Дрешер М. Стратегические игры. Теория и приложения. М.:
Советское радио, 1964.}
.
(при естественном предположении, что стреляющая сторона не была уничтожена противником еще
до своего выстрела). В теории рассмотрены случаи, когда стороны могут
последовательно осуществить несколько выстрелов, обнаруживая факты
промахов противника (в этом случае дуэль называется " шумной ") или
не имея возможностей для такого обнаружения (в этом случае говорят
о " бесшумной " дуэли). Исследования подобных моделей оказали
определенное влияние на содержание наставлений для некоторых родов войск4Дрешер М. Стратегические игры. Теория и приложения. М.:
Советское радио, 1964.}
.
Тем самым, пример, рассмотренный выше, может классифицироваться как шумная дуэль, в которой каждая сторона имеет один выстрел. Заметим, что интерпретация дуэлей как конкурентных взаимодействий появилась значительно позднее5См., например, пособие: Крушевский А.В. Теория игр. Киев: Вища школа, 1977..
В заключение отметим, что успешное вычисление минимаксного и максиминного значений ядра в рассмотренном примере существенно опиралось на специфику конкретной функции (7.2). В общем случае такие вычисления могут оказаться гораздо более сложными. Эти трудности, однако, исчезают, если выбор стратегий (для каждой стороны) ограничен конечным числом вариантов, которые можно перебрать в процессе анализа. Этот случай рассматривается в следующей лекции.


