|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Методы построения функции принадлежности. Обзор основных методов
Косвенные методы для одного эксперта
В обыденной жизни мы часто сталкиваемся со случаями, когда не существует элементарных измеримых свойств и признаков, которые определяют интересующие нас понятия, например, красоту, интеллектуальность. Бывает трудно проранжировать степень проявления свойства у рассматриваемых элементов. Так как степени принадлежности рассматриваются на данном реальном множестве, а не в абсолютном смысле, то интенсивность принадлежности можно определять, исходя из попарных сравнений рассматриваемых элементов.
Среди косвенных методов определения функции принадлежности наибольшее распространение получил метод парных сравнений Саати. Сложность использования этого метода заключается в необходимости нахождения собственного вектора матрицы парных сравнений, которая задается с помощью специально предложенной шкалы. Причем эти сложности увеличиваются с ростом размерности универсального множества, на которой задается лингвистический терм.
Мы рассмотрим метод, также использующий матрицу парных сравнений элементов универсального множества. Но, в отличие от метода Саати, он не требует нахождения собственного вектора матрицы, т.е. освобождает исследователя от трудоемких процедур решения характеристических уравнений.
Пусть  — некоторое свойство, которое рассматривается
как лингвистический
терм. Нечеткое множество, с помощью которого формализуется терм
— некоторое свойство, которое рассматривается
как лингвистический
терм. Нечеткое множество, с помощью которого формализуется терм  ,
представляет собой совокупность пар:
,
представляет собой совокупность пар:
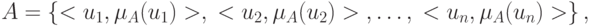
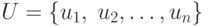 —
универсальное множество, на котором задается нечеткое множество
—
универсальное множество, на котором задается нечеткое множество  .
Задача состоит в том, чтобы определить значения
.
Задача состоит в том, чтобы определить значения 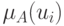 для
всех
для
всех 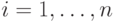 .
Совокупность этих значений и будет составлять неизвестную функцию
принадлежности.
.
Совокупность этих значений и будет составлять неизвестную функцию
принадлежности.Метод, который предлагается для решения поставленной проблемы, базируется на идее распределения степеней принадлежности элементов универсального множества согласно с их рангами. Эта идея раньше использовалась в теории структурного анализа систем, где рассмотрены различные способы определения рангов элементов.
В нашем случае под рангом элемента 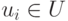 будем понимать
число
будем понимать
число 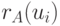 ,
которое характеризует значимость этого элемента в формировании свойства,
описываемого нечетким термом. Допускаем, что выполняется правило: чем больший ранг элемента, тем больше степень принадлежности.
,
которое характеризует значимость этого элемента в формировании свойства,
описываемого нечетким термом. Допускаем, что выполняется правило: чем больший ранг элемента, тем больше степень принадлежности.
Для последующих построений введем такие обозначения: 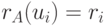 ,
, 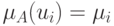 . Тогда
правило распределения
степеней принадлежности можно задать в виде системы соотношений:
. Тогда
правило распределения
степеней принадлежности можно задать в виде системы соотношений:
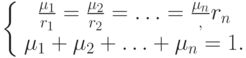
Используя данные соотношения, легко определить степени принадлежности всех элементов универсального множества через степень принадлежности опорного элемента.
Если опорным является элемент 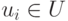 с принадлежностью
с принадлежностью 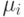 , то
, то

Учитывая условие нормирования, находим:
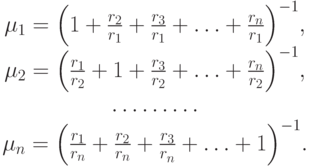
Полученные формулы дают возможность вычислять степени принадлежности
элементов 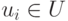 к нечеткому терму
к нечеткому терму  двумя
независимыми путями:
двумя
независимыми путями:
- по абсолютным оценкам уровней
 , которые определяются
согласно методикам, предложенным в теории структурного анализа систем;
, которые определяются
согласно методикам, предложенным в теории структурного анализа систем; - по относительным оценкам рангов
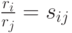 , которые образуют матрицу
, которые образуют матрицу 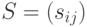 .
.
Эта матрица обладает следующими свойствами:
а) она диагональная, т.е. 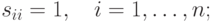
б) ее элементы, которые симметричны относительно главной диагонали, связаны зависимостью 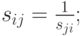
в) она транзитивна, т.е. 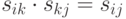 .
.
Наличие этих свойств приводит к тому, что при известных элементах одной
строки
матрицы  легко определить элементы всех других строк. Если
известна
легко определить элементы всех других строк. Если
известна  -я строка, т.е. элементы
-я строка, т.е. элементы 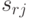 ,
, 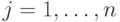 ,
то произвольный элемент
,
то произвольный элемент 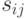 находится так:
находится так:
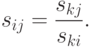
Поскольку матрица  может быть интерпретирована как матрица
парных
сравнений рангов, то для экспертных оценок элементов этой матрицы можно
использовать 9 балльную шкалу Саати. В нашем случае шкала формируется так:
может быть интерпретирована как матрица
парных
сравнений рангов, то для экспертных оценок элементов этой матрицы можно
использовать 9 балльную шкалу Саати. В нашем случае шкала формируется так:
Таким образом, с помощью полученных формул экспертные знания о рангах элементов или их парные сравнения преобразуются в функцию принадлежности нечеткого терма.
Скала предлагает общий метод
варьирования прототипов получения
численного значения функции принадлежности. Пусть имеется прототип
(или идеальный объект)  , описание которого можно деформировать изменением
параметров
, описание которого можно деформировать изменением
параметров 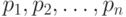 . Если дан некоторый объект
. Если дан некоторый объект  ,
то, варьируя параметры, можно добиться наибольшего соответствия
прототипа и объекта. Вводится мера сходства между объектом
,
то, варьируя параметры, можно добиться наибольшего соответствия
прототипа и объекта. Вводится мера сходства между объектом  и
прототипом
и
прототипом  :
: 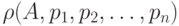 .
.
Для более точного измерения сходства объекта с разными прототипами
вводится штрафная функция  . Далее строится функция:
. Далее строится функция:
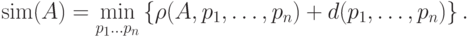
Так как прототип полностью соответствует самому себе, то 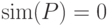 .
Численные значения функции принадлежности вычисляются по формуле
.
Численные значения функции принадлежности вычисляются по формуле
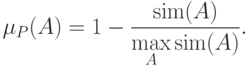

 )
)