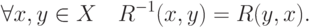|
Зачем необходимы треугольные нормы и конормы? Как их использовать? Имеется ввиду, на практике. |
Нечеткие отношения
Операции над нечеткими отношениями
Объединение и пересечение нечетких отношений определяется следующим образом:
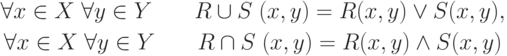
Отношение включения  для нечетких отношений определяется с помощью
отношения частичного порядка на
для нечетких отношений определяется с помощью
отношения частичного порядка на  :
:

Множество 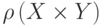 всех нечетких отношений между
всех нечетких отношений между  и
и  образует дистрибутивную решетку по отношению к операциям объединения и
пересечения и удовлетворяет следующим тождествам:
образует дистрибутивную решетку по отношению к операциям объединения и
пересечения и удовлетворяет следующим тождествам:
1. Идемпотентность:




Выполнение этих тождеств для 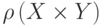 следует из выполнения соответствующих тождеств для решетки
следует из выполнения соответствующих тождеств для решетки  .
В
.
В 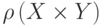 выполняется также следующее соотношение:
выполняется также следующее соотношение:

Из полноты решетки  следует, что она обладает наименьшим 0 и наибольшим I элементами. Эти элементы определяют, соответственно, пустое и универсальное нечеткие отношения:
следует, что она обладает наименьшим 0 и наибольшим I элементами. Эти элементы определяют, соответственно, пустое и универсальное нечеткие отношения:

Следующее соотношение определяет композицию  нечетких
отношений
нечетких
отношений  и
и  :
:

Здесь  обозначает наименьшую верхнюю
грань множества элементов
обозначает наименьшую верхнюю
грань множества элементов 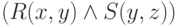 ,
где
,
где  пробегает все значения из
пробегает все значения из  . В силу полноты
. В силу полноты  эта операция всегда определена.
эта операция всегда определена.
Существуют и другие варианты операции композиции, которые определяются с
помощью дополнительных операций, выводимых в  . В зависимости от того,
является ли
. В зависимости от того,
является ли  множеством векторов, множеством лингвистических
переменных или множеством чисел, эти дополнительные операции будут иметь соответствующий
вид. Например, если
множеством векторов, множеством лингвистических
переменных или множеством чисел, эти дополнительные операции будут иметь соответствующий
вид. Например, если  является множеством действительных чисел,
то операция
является множеством действительных чисел,
то операция  может быть заменена на операцию взятия среднего
арифметического, что дает другое определение операции композиции:
может быть заменена на операцию взятия среднего
арифметического, что дает другое определение операции композиции:

В случае ![\(L = \left[ {0,1} \right]\)](/sites/default/files/tex_cache/7a784b60b12d819ade78c757ba656822.png) мы имеем
мы имеем

Замена операции  на операцию умножения дает
следующее определение композиции:
на операцию умножения дает
следующее определение композиции: 
Нечеткое отношение  такое, что
такое, что
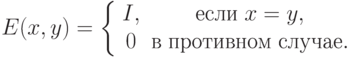
 .
В теории четких отношений отношение Е называется отношением равенства.
.
В теории четких отношений отношение Е называется отношением равенства.Для любого нечеткого
отношения  определяется также обратное
отношение
определяется также обратное
отношение  :
: