Теорема Робертса
Следующая лемма показывает, что значение 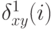 зависит только от
зависит только от

то есть от 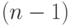 -мерного вектора разностей оценок всех агентов, кроме первого. Вспомним введенные ранее обозначения:
-мерного вектора разностей оценок всех агентов, кроме первого. Вспомним введенные ранее обозначения: 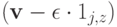 означает оценку
означает оценку 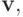 в которой агент
в которой агент 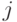 уменьшил значение своей функции для альтернативы
уменьшил значение своей функции для альтернативы 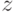 на
на  .
.
Лемма 8.10.
- Для каждого
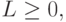
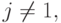
 и всякой тройки различных исходов
и всякой тройки различных исходов 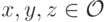
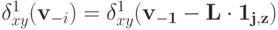 .
. - Пусть
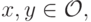 и пусть для некоторых векторов
и пусть для некоторых векторов 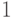 и
и 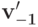 верно, что
верно, что
Тогда
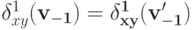 .
.
Доказательство.
- Возьмем
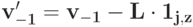 . Если
. Если 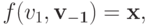 то по S-MON
то по S-MON 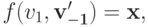 и, следовательно,
и, следовательно,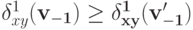 .
.Предположим противное: пусть равенство неверно, а, значит,

Сперва заметим, что, как и в предыдущих доказательствах,

Но
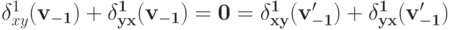 .
.Но мы предполагали, что левая часть этого равенства больше, чем правая; таким образом, мы пришли к противоречию.
- Зафиксируем произвольные векторы
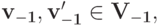
для которых

Для каждого
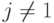 и для каждого
и для каждого  условие S-MON подразумевает, что добавление аддитивной константы ко всем координатам
условие S-MON подразумевает, что добавление аддитивной константы ко всем координатам 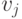 не изменит выбора
не изменит выбора  . Таким образом, мы можем без потери общности предположить, что
. Таким образом, мы можем без потери общности предположить, что 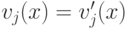 и
и  . Теперь определим
. Теперь определим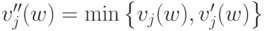
для каждого
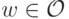 . Тогда первый пункт этой леммы позволяет сделать вывод о том, что
. Тогда первый пункт этой леммы позволяет сделать вывод о том, что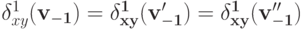 .
.Вот и все, лемма доказана.
Итак, мы доказали, что 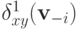 зависит только от
зависит только от  . Таким образом, отныне мы можем рассматривать
. Таким образом, отныне мы можем рассматривать 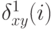 как функцию
как функцию 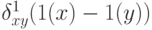 . В этих (слегка измененных) обозначениях можно сформулировать следующее следствие.
. В этих (слегка измененных) обозначениях можно сформулировать следующее следствие.
Следствие 8.2.1. Для любой пары векторов  и любой тройки исходов
и любой тройки исходов 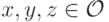 верно, что
верно, что
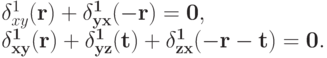
В частности,

Лемма 8.11. Для каждого  и для любой тройки исходов
и для любой тройки исходов 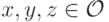
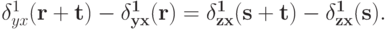
Доказательство. Достаточно показать, что
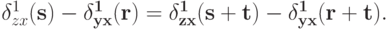
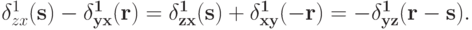
Аналогично,

Теперь нам придется ненадолго отвлечься1Позволю себе, правда, усомниться в слове "придется": есть подозрение, что отвлечься читатель сейчас будет уже очень рад от анализа следствий из условий W-MON и S-MON и доказать небольшое техническое предложение [52], которое нам пригодится на последнем шаге доказательства. Предложение, кстати, само по себе тоже довольно интересное; именно в нем вдруг из каких-то неравенств получается, что функция-то на самом деле линейная.
В формулировке предложения "монотонность" означает следующее: функция 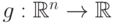 монотонная, если для любых векторов
монотонная, если для любых векторов  из
из  для каждого
для каждого  следует, что
следует, что  . Иначе говоря, это монотонность относительно частичного порядка на векторах, который мы тут уже неоднократно вводили и использовали.
. Иначе говоря, это монотонность относительно частичного порядка на векторах, который мы тут уже неоднократно вводили и использовали.
Предложение 8.1. Зафиксируем монотонную функцию 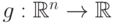 и предположим, что существуют такие функции
и предположим, что существуют такие функции 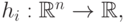 что
что
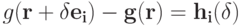
для любого 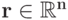 и любого
и любого 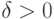 (где
(где  — это единичный вектор вдоль
— это единичный вектор вдоль  -й оси). Тогда существуют такие константы
-й оси). Тогда существуют такие константы 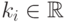 и
и  что
что

Доказательство. Доказательство мы для большей наглядности разобьем на две леммы. Первая из них рассматривает одномерный случай.
Лемма 8.12. Предположим, что 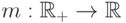 — монотонно неубывающая функция, и существует такая функция
— монотонно неубывающая функция, и существует такая функция 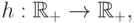 что
что
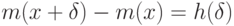
для любых 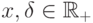 . Тогда существует такое число
. Тогда существует такое число  что
что 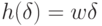 .
.
Доказательство. Пусть 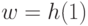 (заметим, что
(заметим, что 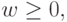 поскольку
поскольку  не убывает). Сначала мы докажем, что для любых двух целых чисел
не убывает). Сначала мы докажем, что для любых двух целых чисел  и
и 
 . Заметим, что
. Заметим, что
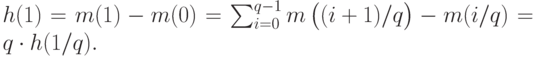
Таким образом,  . Аналогично,
. Аналогично,
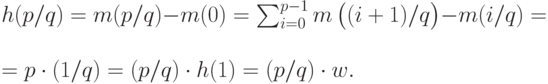
Теперь стандартным образом перейдем по полноте от рациональных чисел к вещественным: докажем, что для любого вещественного 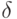
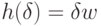 . Заметим, что так как
. Заметим, что так как  монотонно не убывает,
монотонно не убывает,  тоже должна быть монотонно неубывающей. Предположим от противного, что
тоже должна быть монотонно неубывающей. Предположим от противного, что  . Возьмем некоторое рациональное число
. Возьмем некоторое рациональное число  достаточно близкое к
достаточно близкое к 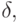 так, что
так, что 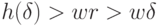 . Так как
. Так как  монотонна, и
монотонна, и  то
то  . Но так как
. Но так как 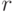 рациональное,
рациональное, 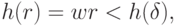 что приводит нас к противоречию. Доказательство совершенно аналогично и при
что приводит нас к противоречию. Доказательство совершенно аналогично и при 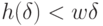 .
.
Лемма 8.13. Рассмотрим подмножество 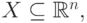 обладающее следующим свойством: если
обладающее следующим свойством: если 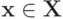 и
и  то
то 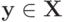 . Рассмотрим монотонно неубывающую функцию
. Рассмотрим монотонно неубывающую функцию 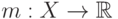 и предположим, что существуют такие числа
и предположим, что существуют такие числа 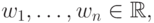 что
что

для любого 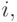 любого
любого 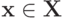 и любого
и любого 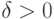 . Тогда существует такая константа
. Тогда существует такая константа  что
что

Доказательство. Сначала мы докажем, что для любых таких 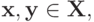 что
что  для всех
для всех 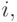 в этом случае
в этом случае
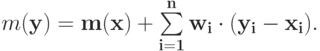
Заметим, что  и
и

Повторяя этот шаг  раз, мы получаем, что
раз, мы получаем, что
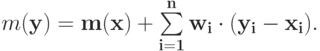
Теперь зафиксируем любой 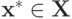 . Докажем, что для любого
. Докажем, что для любого 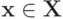
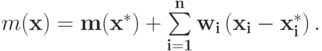
Выберем такой вектор 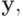 что
что 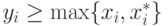 для всех
для всех  . Таким образом,
. Таким образом,
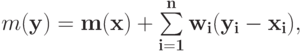
а также
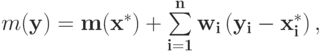
из чего немедленно следует доказываемое утверждение.
Эти две леммы и составляют доказательство предложения 8.1.
Теперь вернемся к доказательству теоремы Робертса. Нам осталось уже буквально одно последнее усилие.
Лемма 8.14. Существуют такие неотрицательные вещественные константы  что для каждого
что для каждого  и для любых исходов
и для любых исходов 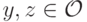
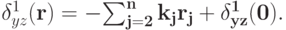
Доказательство. Прежде всего заметим, что  — это монотонно невозрастающая вещественная функция. Если
— это монотонно невозрастающая вещественная функция. Если 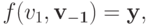 то тогда
то тогда 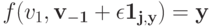 по S-MON. Тогда инфимум на
по S-MON. Тогда инфимум на 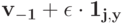 получается на большем множестве, и, следовательно, он меньше. Значит,
получается на большем множестве, и, следовательно, он меньше. Значит,  невозрастает.
невозрастает.
По лемме 8.11 и предложению 8.1 получаем, что существуют такие вещественные константы 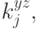 что
что
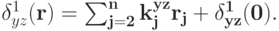
Поскольку  является монотонно невозрастающей функцией, все
является монотонно невозрастающей функцией, все 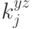 должны быть неположительными. Перепишем для удобства это равенство как
должны быть неположительными. Перепишем для удобства это равенство как
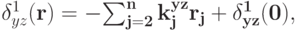
и будем отныне считать, что константы 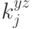 неотрицательны.
неотрицательны.
Нам осталось показать, что 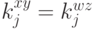 для любых
для любых 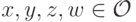 . Выше мы получили, что
. Выше мы получили, что  . По следствию 8.2.1 мы получаем
. По следствию 8.2.1 мы получаем 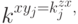 потому что
потому что 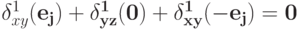 . Аналогично,
. Аналогично, 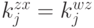 .
.
Теперь мы легко можем завершить доказательство теоремы. Зафиксируем произвольную альтернативу 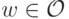 и зададим константы
и зададим константы 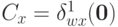 для всех
для всех 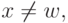 а
а 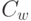 положим равной нулю. Зафиксируем
положим равной нулю. Зафиксируем 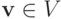 и предположим, что
и предположим, что 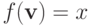 . Следовательно, для любого другого исхода
. Следовательно, для любого другого исхода 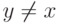

Так как 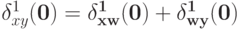 и
и 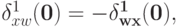 мы, переставляя элементы, получаем, что
мы, переставляя элементы, получаем, что
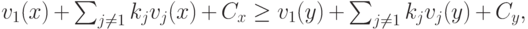
что и требовалось доказать.

