НОУ ИНТУИТ | Теория экономических механизмов. Лекция 1: Теория игр

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 05.08.2011 | Уровень: профессионал | Доступ: платный

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать программу

Аннотация: Прежде чем начинать знакомство с теорией экономических механизмов, придется посвятить некоторое время теории, которая совершенно необходима для понимания всего происходящего в дизайне механизмов. Речь в этой вводной лекции пойдет о теории игр.

Ключевые слова: теория игр, определение, информация, игра, профиль действия, агент, ROCK, paper, scissoring, матрица, игра с нулевой суммой, прибыль, вычет, функция, оптимальная стратегия, response, function, равновесная цена, поле, множества, доминантная стратегия, анализ, равновесие в доминантных стратегиях, аукцион Викри, равновесие Нэша в чистых стратегиях, максимум, дифференциальное уравнение, чистая стратегия, смешанная стратегия, распределение вероятности, интеграл, доказательство, подмножество, евклидово пространство, многозначная функция, неподвижная точка, график, координаты, симплекс, компактное множество, конфликт интересов, компонент, вероятность, совместная смешанная стратегия, доступ, Исход, равновесие в совместных смешанных стратегиях, внешнее устройство, вектор, линейная комбинация, выражение, равновесие по Байесу-Нэшу, равновесие ex post, ex, POST

Основные концепции

Теория игр — наука молодая, хотя, конечно, и не такая молодая, как теория экономических механизмов. Первые шаги на пути к теории игр были сделаны в XVIII веке, первая опубликованная работа относится к первой половине XIX века — это знаменитая книга Антуана Огюстена Курно [14]. Примечательно, что много важных замечаний, относящихся к теории игр, были сделаны биологами, рассматривавшими теорию естественного отбора и поведения животных; поведение было, разумеется, эгоистическим. Классический труд Рональда Фишера [19] содержит многие методы теории игр, а уже после математического оформления этой теории эстафету принял Джон Майнард Смит [46]. Математически же теорию игр оформил Джон фон Нейман: сначала в статьях 1920-х годов [61], а затем в книге с Оскаром Моргенштерном [62], с которой, наверное, и нужно вести историю теории игр как развитого математического аппарата. Учебники по теории игр мы здесь пересказывать не будем, цель этой книги совершенно другая; мы просто изложим вкратце некоторые вещи из теории игр, без которых нам совсем уж не обойтись. А если читатель заинтересуется теорией игр всерьез, рекомендуем ему учебники [20,23,64,65,79].

Дадим формальное определение игр, которые мы будем рассматривать. Кстати, шахматы или даже го не будут подпадать под это определение. Что и логично: мы тут математикой занимаемся, а не эффективными алгоритмами; а с математической точки зрения (да и с точки зрения теории сложности алгоритмов, асимптотической по своей природе) шахматы или го совершенно неинтересны: на конечной доске с конечной продолжительностью партии и с полной информацией выигрышную (или беспроигрышную, если выигрышной нет) стратегию можно "легко" подсчитать простым перебором вариантов.

Игры, которые будем рассматривать мы, тоже обычно подразумевают конечное (или в теории непрерывное, но в реальности все равно конечное, как множество возможных цен, которые игрок может объявить на аукционе) множество возможных стратегий. Но при этом информация принципиально будет неполной; об этом и вся теория. В нашем понимании стратегической игры все игроки будут действовать одновременно, и выигрыш каждого будет зависеть от того, какие стратегии изберут все остальные.

Определение 1.1.Стратегическая игра — это тройка

$\langle \mathcal I, \{ S_i \}_{i\in\cal I}, \{u_i\}_{i\in\mathcal I}\rangle,$

где обозначения расшифровываются следующим образом:

$\mathcal I=\{1,...,N\}$ — конечное множество игроков.
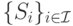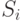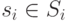$\{S_i\}_{i\in\mathcal I}$ — множество доступных игрокам действий, где — множество действий, доступных игроку . Будем обозначать через $s_i\in S_i$ действие игрока , а через $\mathbf s_{-i}=[s_j]_{j\neq i}$ — вектор действий всех игроков, кроме i^{1Вообще, обозначения вида 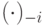в этой книге встречаться будут повсеместно — привыкайте!}. 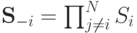Через $\mathbf S = \prod_{i=1}^NS_i$ будем обозначать множество всех векторов действий игроков, через $\mathbf S_{-i}= \prod_{j\neq i}^NS_i$ — множество векторов действий всех игроков, кроме . 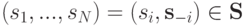Вектор $(s_1,...,s_N) = (s_i,\mathbf s_{-i}) \in \mathbf S$ будем называть профилем действий, или исходом.
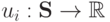$\{u_i\}_{i\in\\mathcal I}$ — множество функций выплат $u_i:\mathbf S\to\mathbb R$ .

Нас будут больше интересовать не действия, а стратегии. Стратегия — это то, как агент выбирает свое действие. В началах теории игр это одно и то же, но в теории экономических механизмов мы будем рассматривать стратегии, представляющие собой вероятностные распределения на действиях или функции, которые принимают во внимание еще и какую-либо дополнительную информацию.

Есть и еще одно важное замечание: в течение этой лекции мы предполагаем, что у участников есть предпочтения по поводу исходов игры и эти предпочтения можно выразить при помощи функций $u_i:S\to\mathbb R$ . Это далеко не всегда так, и в "Теоремы Эрроу и Гиббарда-Саттертуэйта" мы еще поговорим об интересных эффектах, возникающих, когда предпочтения так выразить нельзя. Но для базовой теории игр придется это предположение все-таки сделать.

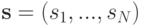Если множество стратегий конечно, то множество исходов игры можно выразить -мерной матрицей, в ячейке которой с координатами $\mathbf s = (s_1,..., s_N)$ стоят исходы 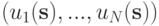$(u_1(\mathbf s),..., u_N(\mathbf s))$ . В случае игры с двумя игроками эта конструкция превращается в самую обычную матрицу.

Пример 1.1. Первый пример возьмем совсем уж из детства — рассмотрим классическую игру "камень-ножницы-бумага"^{2Хотя насчет детства еще можно поспорить: в США вот недавно появилась аж целая ассоциация, посвященная игре в "Rock, Paper, Scissors" под логичным названием USARPS. Призы неплохие — можете попробовать свои силы на сайте http://www.usarps.com/.}. Камень побеждает ножницы, ножницы побеждают бумагу, бумага — камень. У игры получается вот какая матрица (где означает победу того игрока, чьи стратегии выписаны слева, а — победу игрока, стратегии которого стоят в первой строке):

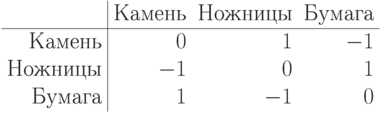
$\begin{array}{r|rrr} & \sdt{Камень} & \sdt{Ножницы} & \sdt{Бумага} \\ \hline \text{Камень} & 0 & 1 & -1 \\ \text{Ножницы} & -1 & 0 & 1 \\ \text{Бумага} & 1 & -1 & 0 \\ \end{array}$

Конец примера 1.1.

Пример 1.2. В качестве второго примера рассмотрим классическую игру полковника Блотто [70,79]. Полковник Блотто должен распределить свои силы ( солдат) между несколькими участками поля боя ( участков). Его противник должен сделать то же самое (количество его солдат может отличаться). Выигрывает тот, кто победит на большем количестве участков боя.

Например, пусть участков боя в игре три, причем и Блотто, и его противник располагает тремя солдатами. Тогда множество стратегий у обоих участников сражения состоит из следующих элементов:

(3,0,0),  (2,1,0),  (2,0,1),  (1,2,0),  (1,1,1),
(1,0,2),  (0,3,0),  (0,2,1),  (0,1,2),  (0,0,3).

В результате у этой игры получается вот какая матрица. Здесь стратегии Блотто изображены слева, противника — сверху; означает, что победил Блотто, — что противник, — случилась ничья.

$\begin{array}{l|rrrrrrrrrr} & \sd{(3,0,0)} & \sd{(2,1,0)} & \sd{(2,0,1)} & \sd{(1,2,0)} & \sd{(1,1,1)} & \sd{(1,0,2)} & \sd{(0,3,0)} & \sd{(0,2,1)} & \sd{(0,1,2)} & \sd{(0,0,3)} \\ \hline (3,0,0) & 0 & 0 & 0 & 0 & -1 & 0 & 0 & -1 & -1 & 0 \\ (2,1,0) & 0 & 0 & 0 & 0 & 0 & 1 & 0 & -1 & 0 & 1 \\ (2,0,1) & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & -1 & 0 \\ (1,2,0) & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ (1,1,1) & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ (1,0,2) & 0 & -1 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ (0,3,0) & 0 & 0 & -1 & 0 & -1 & -1 & 0 & 0 & 0 & 0 \\ (0,2,1) & 1 & 1 & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 \\ (0,1,2) & 1 & 0 & 1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 \\ (0,0,3) & 0 & -1 & 0 & -1 & -1 & 0 & 0 & 0 & 0 & 0 \end{array}$

Конец примера 1.2.

Отметим, что в играх из примеров 1.1 и 1.2 прибыль одного участника строго равнялась убытку второго. Такие игры называются играми с нулевой суммой ; формально говоря, в таких играх для любого профиля действий участников 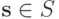$\mathbf s\in S$ верно, что $\sum_{i=1}^Nu_i(\mathbf s) = 0$ .

В дальнейшем нас будут интересовать не только игры с конечными множествами стратегий, но и игры с непрерывными такими множествами. Возьмем классический пример — конкуренцию по Курно (Cournot competition)^{3Этот пример действительно восходит к классику экономической теории Антуану Огюстену Курно [14].}

Рис. 1.1. Конкуренция по Курно: функции оптимального ответа

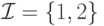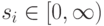Пример 1.3. Рассмотрим рынок некоего продукта, на котором находятся ровно две фирмы: $\mathcal I = \{1,2\}$ . Стратегия каждого из участников — количество продукта, которое он производит: $s_i \in [0,\infty)$ .

Прибыль каждого участника в результате игры — это его общий доход за вычетом себестоимости:

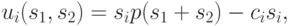
u_i(s_1, s_2) = s_ip(s_1 + s_2) - c_i s_i,

где p(q) — функция, по которой определяется цена, а c_i — цена за единицу для компании . Мы будем предполагать, что c_1 = c_2 = 1 . В качестве функции мы рассмотрим

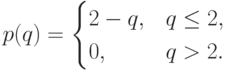
$p(q) = \begin{cases}2-q, & q \le 2, \\ 0, & q > 2.\end{cases}$

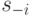Давайте попробуем проанализировать, как фирмам лучше всего играть в свою игру. Попробуем построить оптимальную стратегию для игрока , если игрок произвел товара $s_{-i}$ (best response function, 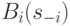$B_i(s_{-i})$ ). Если $s_{-i}>2$ , то производить ничего не надо, потому что равновесная цена все равно будет равна нулю. Если же $s_i\in [0,2]$ , то оптимальную стратегию придется искать так:

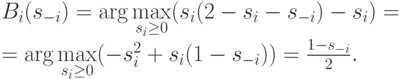
$B_i(s_{-i}) = \arg\max\limits_{s_i\ge 0}(s_i(2-s_i-s_{-i})-s_i) = \\ = \arg\max\limits_{s_i\ge 0}(-s_i^2 + s_i(1-s_{-i})) = \frac{1-s_{-i}}2.$

См. рис. рис. 1.1, на котором мы изобразили эти функции. Интуитивно хочется сказать, что равновесие будет достигнуто в точке их пересечения; но формально мы об этом поговорим ниже.

Конец примера 1.3.

Дальше >>

Теория экономических механизмов

Теория экономических механизмов

Теория игр

Основные концепции

Вопросы и ответы

Студенты

Авторизоваться

Теория экономических механизмов

Теория экономических механизмов

Теория игр

Основные концепции

Вопросы и ответы

Студенты